
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Задача постановка метод алгоритмСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Приведем пример построения алгоритма с одновременным анализом его правильности. Задача: Определить периметр треугольника, заданного на плоскости координатами вершин.
XС,УС
XА,УА Xв,Ув
Постановка задачи
Определение периметра треугольника, заданного на плоскости.
В = (xВ, yВ) - координаты вершин треугольника С = (xС,yС)
Треб.: Р - периметр Метод решения
LАВ = LВС = LСА = где: Р = L(A,B) + L(B,C) + L(C,A); здесь L[(x,y),(u,v)] =
Приведем алгоритм, полученный из описания метода упорядочением операций вычисления длин сторон треугольника с завершающим вычислением периметра. Результаты выполнения алгоритма приведены справа. Алг «периметр треугольника» Нач LAB: = LBC: = LCA: = Р:= LAB + LBC + LCA Кон
Р = LAB + LBC + LCA
Сравнение результатов выполнения алгоритма с описанием метода решения показывает, что это одна и та же система формул, что подтверждает правильность алгоритма. Систематические методы анализа правильности алгоритмов и программ опираются на сопоставление тех же самых описаний, которые используются при их систематическом составлении. Анализ правильности: Задача способ ¯ ¯ Постановка методы ¯ ¯ Сценарий алгоритмы ¯ ¯ ЭВМ ® программа Основные типы алгоритмических ошибок в программах: · ошибки в выбранных методах решения; · ошибки в постановке решаемых задач; · дефекты в сценариях диалога с ЭВМ; · ошибки организации ввода данных; · неправильная реализация методов решения. Исчерпывающий анализ правильности алгоритмов и устранение из программ ошибок всех перечисленных типов возможны только при наличии соответствующих спецификаций: постановок задач, описаний методов решения и спецификаций ввода-вывода данных. Будем считать, что программа правильная, если она дает правильные результаты для любых допустимых исходных данных. Такого рода программы вполне можно использовать для решения прикладных задач. Программа считается надежной, если она не дает сбоев и отказов ни при каких исходных данных. Надежность - обязательное условие для всех программ, которые используются людьми для решения практических задач на ЭВМ.
В качестве иллюстрации приведем пример систематического составления алгоритма и программы задачи определения суммарного веса учеников по данным из таблицы:
Фамилия рост вес
Рассмотрим постановку задачи и метод вычисления суммарного веса. Постановка задачи Определение суммарного веса. Дано: Метод вычисления (D1,.., DN) - данные об учениках, S0 = 0
Fam - фамилия, R - рост, V - вес. [k = (1... N)] Треб.: Vsum - суммарный вес. Vsum = SN Где: Vsum = v1 + v2 +... + vN При: N > 0.
Правильность метода вычислений можно доказать по индукции. Рассмотрим результаты вычислений на 1-м, 2-м и k-м шагах. Отметим, что начальное значение S0 = 0. На первом шаге при k = 1 результат вычисления
S1 = S0 +v1 = v1.
На следующем, втором шаге при k = 2 результат
S2 = S1 + v2 = v1 + v2.
На третьем шаге при k = 3 результат
S3= S2 + v3 = v1 + v2 + v3.
В общем случае можно предположить, что к k-му шагу результат вычисления
Sk-1=v1+...+vk-1.
Тогда результат вычислений после k-го шага (исходя из описания метода)
Sk = Sk-1 +vk = v1 + … + vk-1 + vk.
В силу принципа математической индукции утверждение верно для всех k = 1, 2,.... N. Следовательно, на последнем шаге при k = N конечный результат:
SN = v1 +... + vN.
Что и требовалось. Следовательно, метод правильный.
Приведем сценарий диалога решения поставленной задачи на ЭВМ. Для представления данных в программе примем последовательность операторов data. Сценарий Представление данных
Данные об учениках фамилия вес рост
<Fam1> <V1> <R1> data «Иванов», 185, 85 … … … data «Петрова», 165, 65 <FamN> <VN> <RN> data «Сидоров», 170, 80
суммарный вес = <Vsum>
Алгоритм обработки данных и программа, соответствующие выбранному сценарию и методу вычисления:
АлгоритмПрограмма алг «суммарный вес» ' суммарный вес нач cls вывод («данные об учениках»)? «данные об учениках» вывод («фамилия вес рост»)? «фамилия вес рост» s:= 0 s = 0 цикл do чтение fam$, r, v read fam$, r, v при fam$=«» выход if fam$=«» then exit do вывод (fam$, v, r)? fam$; v; r s:= s + v s = s + v кцикл loop vsum = s vsum = s вывод («суммарный вec=»,vsum)? «суммарный вес=»; vsum кон end Правильность приведенного алгоритма можно увидеть из описания результатов его выполнения.
АлгоритмРезультаты выполнения алг «суммарный вес» на экране и в памяти ЭВМ Нач вывод («Данные об учениках») Данные об учениках вывод («фамилия вес рост») фамилия вес рост
Цикл чтение fam$, r, v при fam$=«» выход вывод (fam$, v, r) <famk> <vk> <rk> s: = s + v sk = sk-1 + vk кцикл [k = (1...n)] vsum = s vsum = sn вывод («суммарный вec=»,vsum) суммарный вес= <vsum> Кон Сопоставление описания результатов выполнения с описаниями сценария и выбранного метода говорит об их полном соответствии. Следовательно, составленные алгоритм и программа правильные.
Вопросы 1. Когда программы содержат ошибки? 2. Что такое правильный способ решения? 3. Когда способ решения неправильный? 4. Что такое правильный метод решения? 5. Когда метод решения неправильный? 6. Что такое правильный алгоритм? 7. Когда алгоритм содержит ошибки? 8. Каковы основные типы ошибок в программах?
Задания 1. Приведите постановку задачи, сценарий, алгоритм и программу решения линейного уравнения а×х + b = 0, с помощью формулы х = -b/а (при а ¹ 0). 2. Приведите постановку задачи, сценарий, алгоритм и программу решения квадратного уравнения а×х2 + b×x + с = 0 с помощью формулы дискриминанта. 3. Приведите постановку задачи, сценарий, алгоритм и программу решения системы из двух уравнений с двумя неизвестными:
с×х + d×y = f. Примените для этой задачи вычисление корней с помощью определителей:
y = Dy/D. Определители D, Dx и Dy вычисляются по формулам:
Dx = e×d - f×b, Dy = a×f - c×e. 4. Приведите постановку, сценарии, алгоритм и программу решения следующих задач: а) определение площади треугольника по длине сторон а, b, с по формуле Герона:
р = (а + b + с)/2.
б) определение площади треугольника, заданного на плоскости координатами своих вершин: (х1, у1), (х2, у2), (х3, у3); для вычисления длин сторон треугольника воспользуйтесь формулой определения длин отрезков на плоскости, задаваемых координатами концов: l =
5. Приведите постановку, метод, сценарий, алгоритм и программу решения следующих задач: а) определение времени встречи пешеходов, двигающихся навстречу друг другу; б) определение времени, которое требуется пешеходу, чтобы догнать другого пешехода; в) определение времени движения парохода по течению и против течения реки; г) определение времени движения пешеходов навстречу друг другу, если один из них движется с замедлением; д) определение времени падения тела с заданной высоты; е) определение времени полета тела, брошенного вверх; ж) определение расстояния, на которое улетит мяч, брошенный под углом к горизонту. 6. Дана прямоугольная матрица АNxM - прямоугольная числовая таблица размера N ´ М. Приведите постановку, метод решения, сценарий, алгоритм и программу для решения следующих задач: а) подсчет сумм элементов матрицы по столбцам, б) подсчет сумм элементов матрицы по строкам, в) нахождение минимального значения в каждом столбце, г) нахождение минимального значения в каждой строке, д) нахождение максимального значения в каждом столбце, е) нахождение максимального значения в каждой строке, ж) нахождение наибольшего из минимальных значений в столбцах, з) нахождение наименьшего из максимальных значений в строках.
Решение прикладных задач
Решение задач на ЭВМ является одним из основных источников для создания алгоритмов и программ. Экономические задачи и проблемы обработки данных - один из важнейших классов прикладных задач, решаемых на ЭВМ. Применение компьютеров для решения экономических задач существенно упрощает работу по подготовке и обработке данных. Одной из причин в использовании ЭВМ для решения этих задач - снижение трудоемкости и уменьшение числа ошибок при обработке данных. Для решения многих экономических задач на ЭВМ используются электронные таблицы и специальные пакеты программ. Однако решение любых новых прикладных задач на ЭВМ предполагает необходимость создания новых алгоритмов и программ на основе определенных математических методов решения и обработки данных. Особое значение правильность алгоритмов имеет для экономических задач, поскольку ошибки в их решении могут дорого стоить. Неправильные экономические расчеты могут нанести материальный ущерб или даже привести к банкротству целую организацию. Для предотвращения ошибок можно использовать систематические методы конструирования алгоритмов и программ с одновременным анализом их правильности. Последовательное применение этих методов обеспечивает составление прикладных алгоритмов и программ с гарантиями их правильности. Общий принцип систематического подхода к составлению алгоритмов и программ заключается в последовательной разработке спецификаций: постановок задач, способов и методов их решения, а также сценариев работы в процессе решения задач.
Составление программ задача ® способы ¯ ¯ постановка ® методы ¯ ¯ сценарий ® алгоритмы ¯ ¯ ЭВМ программы
Систематический анализ правильности алгоритмов и программ сводится к сопоставлению этих спецификаций друг с другом: программ - с алгоритмами, алгоритмов - со сценариями и описаниями методов, а методы решения - с постановками задач. Анализ правильности Задача способ Постановка методы Сценарий алгоритмы ЭВМ ® программы
Приведем примеры систематической разработки алгоритмов и программ решения экономических задач на ЭВМ с обоснованием их правильности. Главной особенностью этих задач является то, что все они относятся к задачам обработки данных. Первый пример экономической задачи - определение средней зарплаты в организации. Допустим, что данные о зарплате представлены таблицей:
Фамилия должность зарплата
Приведем постановку задачи и описание метода вычисления средней зарплаты. Постановка задачиМетод расчета Определение средней зарплаты. Дано: (D1,..., DN) - данные о сотрудниках, где D = [Fam, Т, Z] - состав данных,
Треб: Zcpeдн - средняя зарплата. [k=(l...N)] Где: Zcpeдн = (Z1 +Z2 +... + ZN)/N. Zcpeдн = SN При: N > 0.
Прежде всего убедимся, что выбранный метод вычисления правилен. Для этого воспользуемся индукцией. Рассмотрим результаты вычислений на первых трех шагах.
При k = 1 результат S1=S0∙ (1 - 1)/1 +Z1/1 =Z1/1. При k = 2 результат S2 = S1∙ (2 - 1)/2 + Z2/2 = Z1/2 + Z2/2. При k = 3 результат S3 = S2∙ (3 - 1)/3 + Z3/3 = (Z1 + Z2)/3 + Z3/3.
По этим трем результатам можно утверждать, что в общем случае результатом k-го шага вычислений будет Sk = (Z1 +... + Zk)/k.
Справедливость этого утверждения можно доказать по индукции. Допустим, что оно справедливо для (k-l)-гo шага: Sk-1 = (Z1 +... + Zk-1)/(k-l).
Тогда из описания метода вычислений очередное k-e значение будет равно
Sk = Sk-1∙ (k-l)/k + Zk/k = = (Z1 +... + Zk-1)/(k-l)×(k-l)/k + Zk/k = (Z1 +... + Zk-1)/k + Zk/k.
Что и требовалось доказать. Следовательно, в силу математической индукции это утверждение справедливо для всех k = 1, 2,..., N. В частности, для последнего шага вычислений при k = N конечным результатом будет
SN = (Z1 +... + ZN-1)/N + ZN/N = (Z1 +... + ZN)/N.
Таким образом, выбранный метод дает правильный результат для любой последовательности величин Z1, Z2,..., ZN. Для конструирования алгоритма и программы решения задачи на ЭВМ примем следующий сценарий, а для представления данных воспользуемся операторами data.
СценарийПредставление данных список сотрудников: dan: 'данные сотрудников {<фам> <должн> <з/плата>}* data «Иванов»,«директор», 300000 {...................} data «Петров»,«менеджер», 240000 средняя з/плата= <Zcpeд> data «Сидорова»,«секретарь», 120000 Data «», «», 0
При выбранных сценарии, методе расчета и представлении данных систематическое конструирование приводит к следующим алгоритму и программе: АлгоритмПрограмма алг «средняя зарплата» ' средняя зарплата нач cls вывод («список сотрудников:»)? «список сотрудников:» s:= 0: k:= 0 s = 0: k = 0 цикл do чтение (fam$, dl$, zpl) read fam$, dl$, zpl при fam$ = «» выход if fam$ = «» then exit do вывод (fam$, dl$, z)? fam$; dl$; z k:= k + 1 k = k + 1 s:= s*(k - 1)/k + z/k s = s*(k - 1)/k + z/k кцикл loop zsr = s zsr = s вывод («средняя з/nлama=»,zsr)? «средняя з/плата=»; zsr кон end
Для полного обоснования отсутствия ошибок в приведенном алгоритме и программе приведем описание результатов их выполнения на ЭВМ. АлгоритмРезультаты выполнения Алг «средняя зарплата» Нач
s:= 0: k:= 0 S0 = 0 [ k = 0 ] Цикл чтение (fam$, dl$, z) при fam$ = «» выход вывод (fam$, dl$, z) <famk> <dlk> <zk> }*
s:= s*(k - 1)/k + z/k sk = sk - 1×(k - 1)/k + zk/k Кцикл zsr = s zsr = sN вывод («средняя з/nлama=»,zsr) средняя з/плата= <zsr> Кон
Сравнение результатов выполнения программы с описанием метода вычисления и выбранного сценария подтверждает их соответствие друг другу и как следствие правильности выбранного метода вычислений - правильность составленных алгоритма и программы расчета средней зарплаты.
В качестве второго примера рассмотрим решение типичной задачи подсчета суммарной стоимости товаров с выделением товаров наибольшей стоимости. Допустим, что исходные данные представлены следующей таблицей:
Товар цена кол-во
Приведем постановку задачи и описание способа ее решения.
Постановка задачиСпособ решения Определение суммарной и максимальной стоимости товаров. Дано: (D1,..., DN) - данные о товарах, где D = [Tov, C, M] - состав данных, s0 = 0 Tov - товар, С - цена товара, от k = 1 до N цикл М - количество товара, sk = sk-1 + Сk∙Мk Треб: если k = 1 то Sum - суммарная стоимость товаров, mах1 = С11∙М11 TovMax - товар максимальной инеc Сk ∙ Мk > mахk-1 то стоимости. Где: mахk = Сk ∙ Мk Sum = C1 ∙ M1 + С2 ∙ М2 +... + СN ∙ МN, все TovMax: C×M = Мах(С1 ∙ М1,...,СN ∙ МN). кцикл При: N > 0.
Прежде чем приступить к составлению алгоритмов и программ, убедимся в правильности выбранного способа решения. Для этого проверим результаты на первых шагах, в середине и в конце вычислений. На первом шаге при k = 1 результат
s1 = s0 + С1 ∙ М1 = С1 ∙ M1, max1 = С1 ∙ М1.
На втором шаге вычислений будут получены следующие значения:
s2 = s1 + С2 ∙ М2 = C1 ∙ M1 + С2 ∙ М2,
max1, при С2 ∙ М2 £ max1 = Мах(mах1, С2 ∙ М2).
На третьем и последующих шагах в общем случае будут получаться результаты:
sk = sk-1 + Ck ∙ Mk = C1 ∙ M1 + … + Ck ∙ Mk, maxk = Max(maxk-1, Сk ∙ Мk) = Мах(С1 ∙ М1,..., Сk ∙ Мk).
Для доказательства этих утверждений необходимо предположить, что они выполняются для случая k-1: sk-1 =C1 ∙ M1 +...+ Ck-1 ∙ Mk-1, maxk-1 = Max (C1 ∙ M1, …,Ck-1 ∙ Mk-1),
и подставить эти выражения в соотношения для sk и mахk:
sk = sk-1 + Ck ∙ Mk = C1 ∙ M1 + … Ck-1 ∙ Mk-1 + Ck ∙ Mk, maxk = Max(maxk-1, Сk ∙ Мk) = Мах(С1 ∙ М1,..., Сk ∙ Мk).
В силу математической индукции эти утверждения верны для всех k = 1, 2,..., N. Поэтому на последнем шаге вычислений при k = N будут получены окончательные результаты:
sN = sN-1 + CN ∙ MN = C1 ∙ M1 + … + CN ∙ MN, maxN = Max(maxN-1, СN ∙ МN) = Max(C1 ∙ M1,..., СN ∙ МN). Что и требовалось в постановке задачи. Следовательно, выбранный способ решения поставленной задачи правилен и на его основе можно приступать к составлению соответствующих алгоритма и программы. Для систематичности разработки примем следующий сценарий диалога и представление исходных данных в операторах data. СценарийПредставление данных
список товаров
<тов1> <с1> <т1> * dan: 'сведения о товарах …....... data яблоки, 8000, 3 сумма = <Sum> data бананы, 4000, 2 Максимум data арбузы, 1000, 20 <товар> <стоим> data «», 0, 0
Приведем алгоритм и программу решения поставленной задачи в соответствии с выбранным сценарием и представлением данных. Алгоритм Программа алг «сумма и максимум» ' сумма и максимум нач сls вывод («список товаров»)? «список товаров» вывод («товар цена кол-во»)? «товар цена кол-во» s:= 0; k = 0 s = 0: k = 0 цикл do чтение (тов, с, т) read tv$, с, m при тов = «» выход if tv$ = «» then exit do k:= k + 1 k = k + 1 вывод (тов, с, т)? fv$; с; m s:=s + c ∙ m s= s + c ∙ m если k = 1 то if k = 1 then max:= c ∙ m max = c ∙ m ToвMax:= тов ТМ$ = tv$ инес c ∙ m > max то elseif c(m > max then max:= c ∙ m max = c ∙ m ToвMax:= тов TM = tv$ кесли end if кцикл loop вывод («cyммa=»,s)? «cyммa=»,s вывод («Максимум»)? «Максимум» вывод (ToвMax, max)? TM$, max кон end Сравнение результатов выполнения представленных алгоритма и программы с описанием выбранного способа решения показывает их полное соответствие друг другу. АлгоритмРезультаты выполнения Алг «сумма и максимум» Нач вывод («список товаров») список товаров вывод («товар цена кол-во») товар цена кол-во
Цикл Чтение (тов, с, т)
k:=k+1 [k= 1,2,...,N] вывод (тов, с, т) { <тов> <с> <m> }* s:= s + с×т sk = sk-1 + ck×mk если k = 1 то при k = 1 тах:= c×m max1 = c1×m1 ТовМах:= тов ToвMaх1 = тов1 uнес c×m > тах то при сk×mk > mах тах:= с×т mахk = сk×mk ТовМах:= тов ТовМахk = товk Кесли Кцикл вывод («сумма=», s) cуммa = <sN> вывод («Максимум») Максимум вывод (ТовМах, тах) <ToвMaxN> <maxN> Кон
Из расмотренных примеров следует, что правильность алгоритмов и программ зависит прежде всего от правильности выбранных методов решения. Составление соответствующих им алгоритмов и программ сводится к решению технических проблем. Можно утверждать, что правильные алгоритмы и программы - это корректная реализация правильных методов решения. Ошибки в выбранных методах решения носят не алгоритмический, а принципиальный характер и их следует искать не с помощью отладки программ на ЭВМ, а исследованием самих методов. Рассмотрим самую популярную экономическую задачу - расчет семейного бюджета в целях анализа достатка семьи. Напомним, что достаток семьи - это остаток от разности доходов и расходов:
достаток = доходы - расходы.
Допустим, что данные о семейном бюджете представлены двумя таблицами: - таблицей доходов и таблицей расходов: Доходы Расходы
Приведем точную постановку задачи и опишем метод ее решения. Постановка задачиМетод решения
Дано: S = Sd - Sr D = (дох1,..., дох N) - доходы, Sd = сN
где дох = (имя, d), [k = (1...N)] расх = (стат, r). с0 = 0 Треб.: S - достаток семьи. Sr = bM
S = Sum (d1, …, dN) - Sum (r1,.... rM). [i = (1... M)] При: N, M > 0. b0 = 0
Для решения задачи на ЭВМ в качестве представления данных примем два списка операторов data, а для организации вывода результирующих данных - следующий сценарий. СценарийПредставление данных
Подсчет достатка ' doch: ' доходы
<имяk> <dk> * data «мама», 120000 Data «брат», 200000 Доходов = <Sd> data «», 0 Расходы семьи:
Data «питание», 200000 Расходов = <Sd> data «одежда», 120000 Достаток = <S> data «транспорт», 60000 Data «», 0
Приведем соответствующие этому сценарию и выбранному методу представления данных алгоритмы и программу на Бейсике:
алг «достаток семьи» 'достаток семьи нач cls вывод («Подсчет достатка»)? «Подсчет достатка» вывод («Доходы семьи:»)? «Доходы семьи:» подсчет_доходов gosub dchs 'доходы вывод («Доходов=», Sd)? «Доходов=», Sd вывод («Расходы семьи:»)? «Расходы семьи:» подсчет_расходов gosub rashs 'расходы вывод («Расходов =», Sr)? «Расходов=», Sr S:= Sd - Sr S = Sd - Sr вывод («Достаток=», S)? «Достаток=», S кон end
алг «подсчет доходов» dchs: 'подсчет доходов» нач ' загрузка_доходов restore doch 'доходы Sd:= 0 Sd = 0 цикл do чтение (имя, d) read nam$, d при имя = «» вых if nam$ = «» then exit do вывод (имя, d)? nam$, d Sd = Sd + d Sd = Sd + d кцикл loop кон return
алг «подсчет расходов» rashs ' подсчет расходов нач ' загрузка_расходов restore rach 'расходы Sr:= 0 Sr = 0 цикл do чтение (стат, r) read stat$, r при стат = «» вых if st$ = «» then exit do вывод (стат, r)? st$, r Sr = Sr + r Sr = Sr + r кцикл loop кон return Правильность составленного комплекса алгоритмов и программы расчета достатка семьи можно проверить по описанию результатов их выполнения: «достаток семьи»«подсчет доходов»«подсчет расходов» Подсчет достатка Доходы семьи: Sd0 = 0 [k = 0] Sr0 = 0 [i = 0] <подсчет_доходов>
Расходы семьи: [k =(1...N)] [i =(1...M)] <подсчет_расходов> <имяk> <dk> <статi> <ri> Расходов = < Sr> Sdk = Sd/k-l/+dk Sri == Sri-1 + ri { S = Sd - Sr Достаток = <S>
Для обоснования правильности всего комплекса алгоритмов и программы в целом необходимо показать правильность каждого из вспомогательных алгоритмов: «подсчет доходов» и «подсчет расходов». Для первого алгоритма для первых шагов вычисления получаем:
Sd0 = 0, Sd1 = Sd0 + d1 = d1, Sd2 = Sd1 + d2 = d1 + d2.
Для последующих шагов можно заключить, что
Sdk = Sdk-1 + dk = d1 + d2 +... + dk-1 + dk.
Это доказывается с помощью математической индукции. В силу этого утверждения окончательным результатом вычислений станет сумма доходов
SdN = d1 + d2 +... + dN-1 + dN.
Следовательно, алгоритм подсчета доходов правильный. Для второго алгоритма подсчета расходов получаются аналогичные оценки:
Sr0 = 0, Sr1 = Sr0 + r1 = r1, Sr2 = Sr1 + r2 = r1 + r2,
и для последующих шагов вычислений:
Sri = Sri-1 + ri = r1 + r2 +... + ri-1+ ri.
Это доказывается также с помощью математической индукции. На основании этого утверждения можно сделать заключение о конечном результате выполнения алгоритма:
SrM = r1 + r2 +... + rM-1+ rM.
Следовательно, алгоритм подсчет расходов правильный. Но в основном алгоритме содержится единственная расчетная формула
S = Sd - Sr.
В силу доказанных утверждений о результатах выполнения алгоритмов «подсчета доходов» и «подсчета расходов» конечным результатом вычислений станет величина
S = Sd - Sr = (d1 + d2 +... + dN) - (r1 + r2 +... + rM).
Что и требовалось доказать. Следовательно, весь комплекс алгоритмов и программа в целом правильны.
Вопросы
1. К чему приводят ошибки в экономических программах? 2. Кто отвечает за ошибки в экономических программах? 3. Что дают постановки задач? 4. Зачем нужны описания методов? 5. Как проверяется правильность методов? 6. Зачем нужны описания результатов?
Задания
1. В магазине имеются товары различных наименований. В течение дня каждый из М покупателей (М - заданное число) сообщил о своем намерении приобрести определенное количество товара одного из наименований. Требуется определить суммарный спрос на товары каждого наименования, расположив товары в порядке убывания дневного спроса на них. 2. Каждый из N магазинов в течение месяца работал D дней (N и D - заданные числа 1, 2,.... N). Известна прибыль каждого магазина в каждый день его работы. Необходимо напечатать упорядоченный по месячным доходам список названий магазинов, имеющих прибыль в пересчете на один день работы выше средней дневной прибыли по всем магазинам. 3. Каждое из N предприятий города выпускает М одинаковых наименований продукции (N и М, наименования продукции и названия предприятий известны). Заданы объем выпуска и стоимость единицы продукции каждого вида для каждого из предприятий. Необходимо для каждого вида продукции определить предприятия, выпускающие наибольший объем этой продукции. 4. Из разных городов выбрали N семей (N - заданное число). Каждая семья характеризуется числом членов и доходом каждого изних.Для каждого города сформировать перечень семей с минимальным доходом в пересчете на отдельного члена семьи, указав порядковые номера семей из общего списка. 5. Ассортимент N магазинов состоит из М товаров (N, М и названия товаров заданы). Каждый товар характеризуется наличием или отсутствием его в магазине, а также наличием или отсутствием на него спроса покупателей. Требуется перечислить названия ходовых (есть спрос и товар имеется хотя бы в одном магазине), неходовых (спрос отсутствует, а товар имеется хотя бы в одном магазине) и дефицитных (спрос есть, а товара нет ни в одном из магазинов) товаров.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-16; просмотров: 570; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.139.81.114 (0.018 с.) |


 Дано: А = (xА, yА)
Дано: А = (xА, yА) Р = LАВ +LВС+LСА
Р = LАВ +LВС+LСА ,
,

 .
.

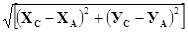
 Результаты
Результаты
 где D = [Fam,R,V] - состав данных, Sk = Sk-1 + vk
где D = [Fam,R,V] - состав данных, Sk = Sk-1 + vk


 dano:'данные учеников
dano:'данные учеников data «», 0, 0
data «», 0, 0 s: = 0 s0 = 0
s: = 0 s0 = 0 а×х + b×у = е,
а×х + b×у = е, х = Dx/D,
х = Dx/D, D = a×d - b×c,
D = a×d - b×c,
 S =
S =  ,
,
 Fam - фамилия, D1 - должность, S0 = 0
Fam - фамилия, D1 - должность, S0 = 0 Z - зарплата. Sk = Sk-1*(k-l)/k + Zk/k
Z - зарплата. Sk = Sk-1*(k-l)/k + Zk/k вывод («список сотрудников:») список сотрудников:
вывод («список сотрудников:») список сотрудников: k:=k + 1 [ k= (1...N) ]
k:=k + 1 [ k= (1...N) ]
 max2 = С2 ∙ М2, при С2 ∙ М2 > max1 = Мах(mах1, С2 ∙ М2),
max2 = С2 ∙ М2, при С2 ∙ М2 > max1 = Мах(mах1, С2 ∙ М2),

 товар цена кол-во
товар цена кол-во s:= 0; k = 0 s0 =0 [k = 0]
s:= 0; k = 0 s0 =0 [k = 0] при тов = «» выход
при тов = «» выход Определение достатка семьи.
Определение достатка семьи. R = (расх1,..., расхМ) - расходы, сk = сk-1 + dk
R = (расх1,..., расхМ) - расходы, сk = сk-1 + dk Где: bi = bi-1 + ri
Где: bi = bi-1 + ri

 Доходы семьи: data «папа», 300000
Доходы семьи: data «папа», 300000
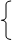 < статk> <rk > * rash: ' расходы
< статk> <rk > * rash: ' расходы



