
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Алгоритм пошуку об’єкта в бінарному деревіСодержание книги
Поиск на нашем сайте
1. Починаємо з кореня дерева. 2. Якщо об’єкт менший від ключа кореня, то переходимо до лівого сина. 3. Якщо об’єкт більший від ключа кореня, то переходимо до правого сина. 4. Якщо об’єкт дорівнює (співпадає) ключу кореня, то він знайдений. 5. Повторюючи кроки 1-4 отримуємо або наявність об’єкта в дереві пошуку або його відсутність. Пошук з поверненням використовують при розв’язуванні задач, в яких відповідь – деяка скінченна множина лементів. Суть алгоритму пошуку з поверненням Нехай розв’язком задачі є множина елементів (x1, x2, …, xn) – впорядкована. Пошук починають з порожньої послідовності (порожньої множини - Нехай знайдені на i-ому кроці значення (x1, x2, …, xi) – деякі часткові розв’язки. На i+1 кроці вибирають (знаходять) таке xi+1, яке не виключає можливість того, що набір (x1, x2 , …, xi, xi+1) можна продовжити до повного розв’язку. Якщо таке значення xi+1 знайдено, то цей процес продовжують для набору (x1, x2 , …, xi, xi+1). Якщо ж такого значення xi+1 не існує, тобто не знайдено, тоді повертаємося до послідовності (x1, x2, …, xi-1) і знаходимо ще невикористане значення xi′ таке, що набір (x1, x2, …, xi-1, xi′) можливо можна продовжити до певного розв’язку. І за скінчену кількість кроків знаходять розв’язок задачі. Або вдалося знайти набір (x1, x2, …, xn), або встановити, що задача не має розв’язку. Задача про мандрівника Гамільтоновим циклом графів, який має n вершин, називається цикл, який містить всі вершини графа по одному разу за виключенням однієї, яку містить два рази. Задача про мандрівника полягає в тому, щоб знайти при заданій сітці доріг між містами такий його шлях, який дає змогу мандрівнику, вийшовши з деякого міста, побувати в кожному місті один раз і повернутися назад. Приклад 1 Побудувати гамільтонові цикли для графа (мал. 33).
Задача про розфарбування графа в n кольорів Потрібно встановити чи можна розфарбувати вершини графа в один із n заданих кольорів таким чином, щоб вершини, які з’єднані ребрами мали різний колір. Під плоским графом розуміють граф, в якому ребра в певному розумінні не перетинаються між собою. Встановлено, що кожний такий граф можна розфарбувати в 4 кольори. Ідея використання пошуку з поверненням для розфарбування графа
a, b, c – вершини графа. Спочатку розфарбовують вершину a в певний колір, потім вершину b в перший колір, якщо вона несуміжна з a, і в другий, якщо суміжна з a. Вершину c розфарбовують в перший колір, якщо можливо, або в другий, якщо не можливо в перший. Якщо ж і це неможливо, то в третій. Якщо на деякому кроці неможливо розфарбувати деяку вершину в певний колір, то повертаються до попередньої і змінюють колір цієї вершини на наступний. Приклад 2 Розфарбувати граф в 3 кольори.
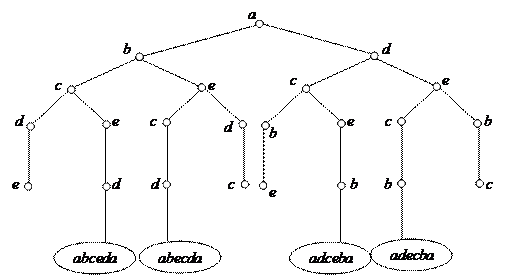
Задача про ферзів Нехай маємо шахову дошку розміром n* n. По цій дошці потрібно розмістити n ферзів, який не били б один одного, тобто, щоб на жодній вертикальній чи горизонтальній смузі клітинок не містилось два ферзя, і на кожній діагоналі. Алгоритм розв’язку з використанням бектрекінгу 1. Починають з порожньої шахівниці. Нехай в k перших стовпчиках ферзі розставлено. На k+1 кроці ставлять ферзя на першій верхній клітинці k+1 стовпчика. 2. Якщо k+1 ферзів не б’ють один одного, то переходять до наступного кроку. Якщо це не так, то ферзя в k+1 стовпчику ставлять в другій верхній клітинці і т. д. 3. В тому випадку, коли ферзя не можна розмістити в жодній клітинці k+1 стовпчика, повертаються до k – ого кроку. Переміщають ферзя в k-ому стовпчику на одну клітинку вниз і переходять до k+1 кроку. Якщо таке переміщення ферзя не дає змогу розмістити його в k+1 стовпчику, тоді ферзя на k-ому стовпчику переміщають на ще одну клітинку вниз. Приклад 3 n=4
Мал. 37. Алгоритм пошуку з поверненням можна також використати для розв’язання задачі знаходження суми елементів підмножин деякої множини. Приклад 4 Нехай маємо деяку скінченну множину натуральних чисел A. І задане деяке натуральне число M. Знайти підмножини множини A, сума елементів яких дорівнює M.
Відношення 1. Відношення та їх властивості. 2. Відношення еквівалентності. 3. Операції над відношеннями. Нехай A, B множини. Відношенням з множини A в множину B називається підмножина декартового добутку множин A і B.
Зауваження Відношення з A в B інколи називають бінарним відношенням. А відношення між m множинами називається m-арним відношенням.
Приклад 1 А={1, 2, 3}, B={a, 0} R={(1,a), (2,0), (3,0)} Якщо A=B, тоді говорять, що мають відношення на множині А. Приклад 2 А={1, 2, 3, 4} R позначає, що A перебуває у відношення з B, якщо A ділить B. R={(1, 2), (1, 1), (1, 3), (1, 4), (2, 2), (2, 4), (3, 3), (4, 4)} Кожному відношенню можна поставити і відповідність граф, де ребра графа (дуги) це елементи відношення.
Кожному відношенню на множині можна поставити у відповідність матрицю, елементи якої визначаються:
Відношенням R називається рефлексивним, якщо для Приклад 3 A={1, 2, 3, 4} R1= {(1,1), (1, 2), (2, 1), (2, 2), (3, 4), (4, 1), (4, 4)} R2= {(1, 1), (1, 2), (2, 1)} R3= {(1, 1), (1, 2), (1, 4), (2, 1), (2, 2), (3, 3), (4, 1), (4, 4)} R4= {(2, 1), (3, 1), (3, 2), (4, 1), (4, 2), (4, 3)} R5= {(1, 1), (1, 2), (1, 3), (1, 4), (2, 2), (2, 3), (2, 4), (3, 3), (3, 4), (4, 4)} R6= {(3, 4)} R3, R5 – рефлексивні відношення. Відношенням R на множині називається симетричним якщо R3, R2 – симетричні відношення. Відношенням R на множині називається іррефлексивним якщо R4, R6 – іррефлексивні відношення. Відношенням R на множині називається асиметричним якщо R4, R6 – асиметричне відношення. Відношення A називається транзитивним, якщо R4, R5, R2 – транзитивні відношення. Кожне з відношень є рефлексивним чи іррефлексивним, симетричним чи асиметричним. Відношенням R на множині A називається відношенням еквівалентності, якщо воно рефлексивне, симетричне і транзитивне. Приклад 4 Відношення на R задане наступним чином:
1. aRa a=a 2. aRb a=b b=a 3. aRb (a=b Використовуючи властивості диз’юнкціїї та кон’юнкції, отримаємо aRc. Отже, задане відношення є відношенням еквівалентності. Приклад 5 Відношення R на множині дійсних чисел задане:
1. 2. aRb
3. aRb
a – c = (a – b) + (b – c) Дане відношення є відношенням еквівалентності. Приклад 6 Відношення R на множині цілих чисел, яке задається:
1. 2.
3.
Дане відношення є відношенням еквівалентності. Нехай R – відношення еквівалентності на множиніA. Кожний елемент Класом еквівалентності елемента a (породженого елементом а) називають множину всіх елементів множини A, які еквівалентні з елементом a.
Приклад Описати класи еквівалентності у відношеннях aRb [1] = {1; -1} [-3,5] = {-3,5; 3,5}
Зауваження Множину, кожний елемент якої є класом еквівалентності при даному відношенні можна в деякому розумінні ототожнити з множиною невід’ємних дійсних чисел. Приклад Побудувати класи еквівалентності для відношення на Z
Всі решта класів співпадають. Зауваження На множині класів еквівалентності можна ввести операції додавання, множення. При цьому будемо мати: [1]+ [2]= [3] [2]+[4]=[1] [3]+[2]=[0] [2]*[2]=[4] [2]*[3]=[1]
Нехай R відношення еквівалентності на множині А, тоді еквівалентні наступні співвідношення: I. aRb II. [a]=[b] III. Нехай R відношення еквівалентності на множині А. Множину А можна представити у вигляді
Тобто відношення еквівалентності розбиває множину на сукупність підмножин, які не перетинаються між собою. В деяких випадках на такому розбитті множини можна ввести операції, які були б властиві елементам множини А. В результаті отримують нову множину, в якій н6ад елементами можна виконувати операції, які аналогічні операціям над елементами самої множини.
Нехай A, B – множини. Оскільки відношення R підмножина добутку A´B Нехай R1, R2 – відношення з множини А на множину В. Об’єднанням
Приклад А={1, 2, 3} В={1, 2, 3, 4} R1={(1, 1), (2, 2), (3, 3)} R2={(1, 2), (1, 1), (1, 3), (1, 4)}
Зауваження Відношення з множини А в B можна вважати в певному розумінні деякою функцією. Нехай R – відношення з A в B, а S – відношення з B в C. Суперпозицією відношень R та S називають таке відношення
Нехай M1 і M2 – булеві матриці однакових розмірів. Диз’юнкцією мулевих матриць
Кон’юнкцією мулевих матриць
Об’єднанням відношень (перетин) відповідає диз’юнктивна (кон’юнктивна) булева матриця. Суперпозиції відображень відповідає булевий добуток матриць, який відповідає цим відображенням.
|
|||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-28; просмотров: 132; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.216.112 (0.008 с.) |

 ).
).





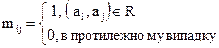
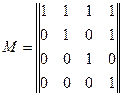
 має місце aRa, тобто кожний елемент перебуває у відношенні сам з собою.
має місце aRa, тобто кожний елемент перебуває у відношенні сам з собою.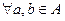 з того, що aRb випливає bRa.
з того, що aRb випливає bRa.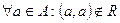
 випливає
випливає 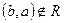 .
. з того, що
з того, що  випливає aRc.
випливає aRc.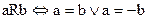

 a=b
a=b  a=-b
a=-b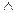 bRc
bRc 


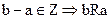

 Z
Z
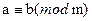 - різниця цих чисел – число, кратне m.
- різниця цих чисел – число, кратне m.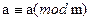




 перебуває у відношенні хоча б з одним елементом (рефлективність відношення означає aRa).
перебуває у відношенні хоча б з одним елементом (рефлективність відношення означає aRa). - клас еквівалентності.
- клас еквівалентності.

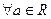 [a] = {a; -a}
[a] = {a; -a} [0] = {0}
[0] = {0}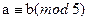
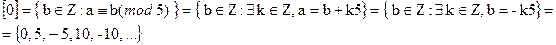






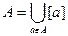
 , то на нього можна розповсюдити операції, які повязані з множинами.
, то на нього можна розповсюдити операції, які повязані з множинами. називається відношення, яке задає підмножина декартового добутку:
називається відношення, яке задає підмножина декартового добутку:
 ={(1, 1)}
={(1, 1)} ={ (2, 2), (3, 3)}
={ (2, 2), (3, 3)} , елементами якого є пари (a, c) такі, що існує елемент
, елементами якого є пари (a, c) такі, що існує елемент  , де aRb та bRc.
, де aRb та bRc.
 називається булева матриця, елементи якої визначаються
називається булева матриця, елементи якої визначаються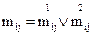
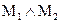 називається булева матриця, елементи якої визначаються
називається булева матриця, елементи якої визначаються



