Задача про Кенінгсберські мости

Чи можна з будь-якої частини міста повернутися назад, пройшовши кожен із мостів один раз?

Ейлер при розв’язанні цієї задачі поставив у відповідність розташуванню мостів у місті мультограф.

 

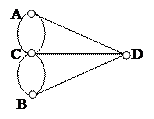
Мовою графів задача про Кенінгсберські мости формулюється:

Чи існує в мультографі простий цикл, який містить всі його ребра?

Ейлеревим циклом у зв’язному мультографі називається простий цикл, який містить усі ребра графа.

Зв’язний мультиграф має ейлерів цикл тоді і тільки тоді, коли степені усіх його вершин парні.

Зваженим називається простий граф, в якому кожному ребру e відповідає деяке число w(e), яке називається його вагою.

В більшості випадків число w(e) вважають додатнім.

Зваженим орієнтованим графом називається граф, в якому кожній дузі e ставиться у відповідність число w(e).

В зваженому орієнтованому графі довжини дуг можуть бути як додатними, так і від ємними числами.

Вагою шляху (циклу) або довжиною називають суму ваг ребер (дуг), який утворюють цей шлях (цикл).

Задача про найкоротший шлях

Знайти найкоротший шлях від заданої початкової вершини a до кінцевої вершини z у зв’язному (сильнозв’язному) графі.

З цієї задачі випливають наступні задачі:

1. Знайти найкоротші шляхи від заданої вершини a до всіх інших вершин.

2. Знайти найкоротші шляхи між всіма можливими парами вершин графа.

Алгоритм Дейстри

Починаючи з вершини a до кінцевої вершини a знаходимо відстань до кожної суміжної з нею вершини. Вибираємо вершину, віддаль від якої до вершини a найменша. Нехай це буде вершина V.

При цьому для кожної вершини записуємо знайдені віддалі від вершини a. Знаходимо віддалі від a до кожної із суміжних з вершиною V вершин по шляхах, які проходять через вершину V.

Якщо для деяких вершин знайдені віддалі менші від тих, які записані біля вершини, то їх замінюємо на знайдені.

Серед знайдених віддалей знову вибираємо вершину з найменшою віддалю і т. д.

 

Якщо при знаходженні найкоротшої відстані від a до z отримали біля всіх вершин відстані, взяті у кружечки, то тим самим розв’язали задачу знаходження відстані від a до всіх інших вершин.

 

Дерева

1. Поняття «дерево» та його властивості.

2. Рекурсія. Обхід дерев.

3. Форми запису виразів.

Деревом називається зв’язний граф, який не містить простих циклів.

 

 

 

Зауваження

З означення випливає, що дерево є простим графом.

Теорема (еквівалентні означення дерева)

Нехай T – граф, який має n вершин.

Наступні твердження еквівалентні:

1. T – дерево.

2. T - зв’язний граф і має n-1 ребро.

3. T не містить простих циклів і має n-1 ребро.

4. Довільні дві вершини графа T зв’язані одним простим шляхом.

5. T – зв’язний граф, але вилучення довільного його ребра приводить його до незв’язного графа.

Розглянемо поняття кореневого дерева.

Розглянемо T – дерево, v – одна з його вершин.

Оскільки до будь-якої іншої вершини дерева існує єдиний простий шлях, який з’єднує цю вершину з вершиною v, тоді можна вважати, що таке дерево (граф) є орієнтованим. Причому орієнтація здійснюється на ребрах з врахуванням цих простих шляхів.

Вершину v називають коренем дерева.

Кореневим деревом називається дерево разом з виділеним коренем (орієнтований граф).

Зауваження

Якщо задано дерево, то при кожному виборі кореня отримують різні кореневі дерева (орієнтовані графи).

 

а) б) в)

а) дерево; б) d – корінь; в) g – корінь;

Нехай T – кореневе дерево.

Батьком вершини u, яка відмінна від кореня дерева, називається така вершина v, що (v u) – ребро орієнтованого графа.

Якщо v батько u, то u – син v.

Аналогічно можна ввести поняття діда, внука, прадіда, правнука.

Вершина кореневого дерева, яка не має синів, називається листком.

Вершини кореневого дерева, які не є листками, називаються внутрішніми.

Корінь дерева є внутрішньою вершиною.

Якщо a – вершина дерева, то під піддеревом з коренем a, розуміють граф, що містить a та всі вершини, що є нащадками a, а також ребра, що їх з’єднують.

Під m-арним деревом розуміють кореневе дерево, в якому кожна внутрішня вершина має не більше, ніж m синів.

Повним m-арним деревом називається дерево, в якого кожна внутрішня вершина має рівно m синів.

Якщо кореневе дерево є бінарним, тоді синів кожного батька впорядковують, тобто кожного з них називають лівим, а другого – правим.

Об’єкт називається рекурсивним, якщо він містить сам себе, або визначений за допомогою самого себе.

Приклад

Введемо означення бінарного дерева, використовуючи рекурсію.

Ізольована вершина є бінарним деревом. Нехай A, B – бінарні дерева. Тоді конструкція є бінарним деревом.

 

 

Причому повним, якщо A і B повні бінарні древа.

Зауваження

При означенні рекурсивного об’єкта в основному використовують наступний принцип.

Спочатку вказують елементарний рекурсивний об’єкт, а потім задають правило (алгоритм), за яким визначається складніший рекурсивний об’єкт через раніш заданий простіший.

Приклад

0!=1

n!=n(n-1)!

В багатьох задачах для знаходження розв’язку потрібно здійснити обхід всіх вершин кореневого дерева.

Тому виникає задача про знаходження алгоритму (способу) обходу всіх вершин кореневого дерева.

Розглянемо найпростіші способи обходу бінарного кореневого древа.

 

 

Нехай маємо бінарне кореневе дерево, задане рекурсією.

1. Прямий обхід або обхід зверху вниз задається послідовністю R, A, B.

2. Внутрішній обхід або обхід зліва направо задається A, R, B.

3. Обхід у зворотньому порядку або знизу вверх задається A, B, R.

Приклад

 

 

1. Зверху вниз

dackmnbefsp

2. Знизу вверх

cmnkaespfbd

При використанні алгебраїчних та логічних виразів в програмах виникає проблема їх представлення.

В більшості випадків ці представлення використовують бінарні або m-арні дерева, які представляються у вигляді певних записів.

Приклад

При представленні виразу у вигляді бінарного дерева змінні та операції виступають вершинами дерева, а порядок виконання задає орієнтацію ребер, які з’єднують ці вершини.

При обході дерев, які відповідають деяким виразам, отримують записи, які мають певну назву.

1. Зверху вниз – польський запис (префіксний).

2. Знизу вверх – зворотній польський запис (постфіксний).

Приклад

Польський запис

*+a/bc-d*ef

Зауваження

При заданому польському записі виразу побудувати сам вираз або дерево, яке йому відповідає.

Для обчислення значення виразу в польському записі його розглядають справа наліво, знаходять дві величини (числа), які записані поряд, а після них розміщений символ операції.

Виконують операцію над цими числами, після цього в цьому записі операцію і два символи замінюють отриманими значеннями.

На останньому кроці отримують значення виразу.

Приклад

Обчислити значення виразу в польському записі.

+-*235/↑234

Крок	Вираз	Виділені символи	Виконані операції
	+-*235/↑234	↑23	2^3=8
	+-*235/84	/84	8/4=2
	+-*2352	*23	3*2=6
	+-652	-65	6-5=1
	+12	+12	1+2=3

При обчисленні виразу, який заданий зворотнім польським записом, алгоритм такий самий, тільки обхід зліва направо.

 

Пошук в деревах

1. Бінарне дерево пошуку.

2. Пошук з поверненням (бектрекінг).

При означення дерева кожній вершині відповідало певне ім’я, яке не відігравало суттєвої ролі (імена можна змінювати довільним чином).

В задачах пошуку вершини дерева з певним ім’ям в загальному випадку потрібно переглянути (перевірити) всі вершини.

Для спрощення встановлення вершини дерева з певним іменем (значенням) використовують бінарні дерева пошуку.

При побудові таких дерев вважають, що вершини дерева мають імена та значення, які лінійно впорядковані.

Множина M називається лінійно впорядкованою, якщо кожні два її елементи можна порівняти між собою, тобто визначити (встановити), який елемент більший, а який менший.

У бінарному дереві пошуку кожній вершині присвоюються певні значення (ключі).

Ключ – елемент з деякої лінійно впорядкованої множини.

Бінарне дерево пошуку будують рекурсивно.

Кожна вершина дерева розбиває його на два піддерева, причому ліве піддерево містить ключі, які менші від ключа вершини дерева, а праве піддерево – ключі, що більші ключа вершини.

Ця властивість повторюється рекурсивно для кожної вершини дерева.

Приклад

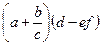
Побудувати бінарне дерево пошуку для списку слів: математика, фізика, зоологія, метеорологія, біологія, психологія, хімія.