
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Алгоритм знаходження НСК двох чиселСодержание книги
Поиск на нашем сайте
Алгоритм Евкліда Нехай а і в нерівні нулю одночасно, причому а>в: 1)ділимо число а на число в; знаходимо неповну частку і остачу. 2)ділимо число в, отримуємо неповну частку і остачу. 3)ділимов на q. Продовжуємо цей процес до того часу доки не отримаємо в остачі 0. Тоді НСД чисел а і в дорівнює останній відмінній від нуля остачі в алгоритмі Евкліда.
Алгоритм знаходження НСК двох чисел 1.Розкласти числа на прості множники. 2.Записати всі множники з першого числа, а з другого виписати ті яких немає в першому. 3.Знаходимо добуток цих чисел. Якщо одне з двох натур. Чисел ділиться на друге число, то більше з цих 2 чисел є НСК. Якщо 2 числа є взаємопростими, то найменше спільне кратне дорівнює їх добуток. 4. Властивості множення та ділення додатних раціональних чисел. Будь-яке від’ємне число менше нуля і будь-якого додатного числа. Нуль менше будь-якого додатного числа. Наприклад: -5<0; -5<1; 0<10. Ділення додатних і від’ємних чисел 5. Кон’юнкція та диз’юнкція двох предикатів. Множина істинності кон’юнкції та диз’юнкції двох предикатів. Предикатом називається висловлювання з змінною, яке перетворюється в істинне або хибне висловлення при підстановці замість змінної конкретного значення. «х>5»-предикат, «6>5»-істинне, «3>5»-хибне. Множиною істинності предикату А(х) наз. множина значень змінної при яких предикат перетворюється в істинне висловлювання. ТА(х)≤х пр: А(х): Кон’юкцію двох предикатів А(х) і В(х) визначених на множині Х називається предикат виду А(х)˄ В(х), який перетворюється в істинне висловлення тоді, коли кожен з предикатів перетвориться в істинне висловлення. Множиною істинності предикатів буде переріз множин ТА(Х)˄В(Х) = ТА(Х)∩ТВ(Х) Прикладом кон’юкції двох предикатів є с-ма рівнянь або нерівностей Диз’юнкцією двох предикатів А(х) і В(х) називається предикат виду А(х)˅В(х), який перетворюється в істинне висловлення при тих значеннях змінних при яких хоча б один з предикатів стає істинним. Прикладом диз’юнкції предикатів є сукупність нерівностей Очевидно, що множину істинності кон’юкції та диз’юкції двох предикатів знаходять за формулами: ТА(Х)˄В(Х) = ТА(Х)∩ТВ(Х) ТА(Х)˄В(Х) = ТА(Х) 6. Ознаки подільності на складені числа (6,12,18) Ознака подільності на 6 Число ділиться на 6 тоді і тільки тоді, коли воно ділиться і на 2, і на 3, тобто якщо воно парне і сума його цифр ділиться на 3. Нариклад: 462, 3456, 24642 — діляться на 6, так як вони діляться одночасно і на 2, і на 3; 861, 3458, 34681 — не діляться на 6, так як 861 не ділиться на 2, 3458 не ділиться на 3, 34681 не ділиться на 2. Ознака подільності на 12. Для того щоб число х ділилося на 12, необхідно і достатньо, щоб воно ділилося на 3 і 4. Ознака подільності на 18. Для того щоб число х ділилося на 18, необхідно і достатньо, щоб воно ділилося на 2 і 9. 7. Розклад числа на прості множники. Основна теорема арифметики. Означення. Розкладом натурального числа n на прості множники (факторизацією числа) називається представлення його у вигляді n = Задача перевірки числа на простоту є простішою за задачу факторизації. Тому перед розкладанням числа на прості множники слід перевірити число на простоту. Означення. Розбиттям числа називається задача представлення натурального числа n у вигляді n = a * b, де a, b – натуральні числа, більші за 1 (не обов’язково прості). Метод Ферма Нехай n – складене число, яке не є степенем простого числа. Метод Ферма намагається знати такі натуральні x та y, що n = x2 – y2. Після чого дільниками числа n будуть a = x – y та b = x + y: n = a * b = (x – y)(x + y). Якщо припустити що n = a * b, то в якості x та y (таких що n = x2 – y2) можна обрати Тоді x = (13 + 11) / 2 = 12, y = (13 – 11) / 2 = 1. Перевірка: x2 – y2 = 122 – 11 = 143 = n. Теорема. Якщо n = x2 – y2, то < x < (n + 1) / 2. Доведення. З рівності n = x2 – y2 випливає, що n < x2, тобто < x. Оскільки a = n / b, то. Максимальне значення x досягається при мінімальному b, тобто при b = 1. Звідси x = <. Отже для пошуку представлення n = x2 – y2 слід перебрати всі можливі значення x із проміжку [, (n + 1) / 2], перевіряючи при цьому чи є вираз x2 - n повним квадратом. Приклад. Розкласти на множники n = 391 методом Ферма. = 19. 202 – 391 = 9 = 32. Маємо рівність: 391 = 202 – 32. Звідси 391 = (20 – 3)(20 + 3) = 17 * 23. Основна теорема арифметики стверджує, що будь-яке натуральне число більше одиниці може бути представлене у вигляді добутку простих чисел і таке представлення є єдиним з точністю до порядку множників. Для знаходження розкладу натурального числа на прості множники послідовно застосовується операція ділення числа на прості числа починаючи з найменшого. Причому, перехід до наступного більшого простого числа виконується тільки при неможливості цілого ділення на менше. Так, наприклад, можна отримати наступні розклади чисел 420 та 1200: Згідно з основною теоремою арифметики стверджується, що ці представлення є унікальними для кожного числа, тобто не існує розкладів з іншим набором чисел або іншою кількістю однакових множників. Відрізнятися може лише порядок множників, але, внаслідок комутативності та асоціативності множення, всі такі розклади є еквівалентними. Таким чином, теоремою стверджується, що не існує таких чисел, які можна було б розкласти на прості множники різними способами. 8. Відношення логічного слідування рівносильності на множині предикатів. Необхідні і достатні умови. Логічне слідування А(х) то В(х) означає, що з істинності А(х) обов’язково випливає істинність В(х), тобто А(х) є достатньою умовою для В(х), а В(х) необхідно випливає з А(х). А(х) → В(х) х:4→х:2 «Для того, щоб число ділилося на 2, для нього достатньо, щоб воно ділилося на 4» «Для того, щоб число ділилося на 4, необхідно, щоб воно ділилося на 2» А(х) → В(х) «Для того, щоб прямокутник був квадратом необхідно, щоб він був прямокутником» «Для того, щоб квадрат був прямокутником достатньо, щоб він був квадратом» У цих випадках не буде істинною обернена імплікація В(х) ≠ А(х) Але є логічні слідування які виконуються в обидві сторони: А(х): «х:3» В(х): «сума цифр: 3» А(х) → В(х) – істинна Якщо число ділиться на 3, то й сума цифр ділиться на 3. В(х)→А(х) – істинна Якщо сума цифр діл на 3, то й число діл на 3. Отже, істинною є еквіваленція цих предикатів, це означає, що можна записати предикати А(х) ↔ В(х) «число діл на 3, тоді і тільки тоді, коли сума його цифр діл на 3» або «для того, щоб число діл на 3, необхідно і достатньо, що сума цифр діл на 3». Теорема 5. Предикати P(x) і Q(x) рівносильні тоді і тільки тоді, коли кожний з них є логічним наслідком іншого. Якщо предикати P(x) і Q(x), визначені на множині M, такі, що предикат Q(x) є логічним наслідком предиката P(x), то предикат Q(x) називається необхідною умовою для предиката P(x), а предикат P(x) – достатньою умовою для предиката Q(x). Необхідна умова може не бути достатньою, а достатня – необхідною. Якщо з предиката P(x) логічно випливає предикат Q(x) і з предиката Q(x) логічно випливає предикат P(x), тобто вони рівносильні, то предикат Q(x) називається необхідною і достатньою умовою для предиката P(x), а предикат P(x) – необхідною і достатньою умовою для предиката Q(x). 9. Обернена пропорційність. Застосування до розв’язування задач в початковій школі. Функція виду у= Обернено пропорційна залежність між двома величинами означає що із збільшенням (зменшенням) однієї величина друга зменшується (збільшується) у стільки ж разів. Пр: 3 друкарки виконали роботу за 4 год. За скільки годин виконають цю ж роботу 6 друкарок? Чим більше друкарок, тим швидше вони виконають роботу. Це означає, що між кількістю робочої сили і часом існує обернено пропорційна залежність. 3 др – 4 год 6 др -? год 1) 6:3=2(р)-у стільки раз збільшилося друкарок; 2) 4:2=2(год)- для 6 друкарок. Обернено пропорційні величини є такі: 1)к-сть робочої сили і затрачений час; 2)швидкість руху і затрата часу; 3)ціна і к-сть товару на ті самі гроші; 10. Нескінченні періодичні десяткові дроби. Умова, при якій звичайний дріб перетворюється в періодичний. Щоб перетворити звичайний дріб у десятковий, достатньо його чисельник поділити на знаменник. Якщо при діленні чисельника на знаменник матимемо нескінченний дріб, у якого одна або кілька цифр повторюються в одній і тій же послідовності, то такий дріб називають періодичним. У таких випадках говорять про наближене перетворення звичайних дробів у десяткові. Чистий періодичний дріб — такий дріб, у якого період починається одразу після коми, мішаний — такий, у якому між комою і періодом є одна або кілька цифр, що не повторюються. Якщо в розкладі на прості множники знаменника звичайного дробу є лише числа 2 і 5, то такий дріб перетворюється у скінчений десятковий дріб. Нескінченний періодичний десятковий дріб – десятковий дріб, у якому нескінченно повторюється певна група цифр. Мінімальна група цифр, яка повторюється, називається періодом. Період записується в круглих дужках. Якщо в розкладі на прості множники знаменника звичайного нескоротного дробу, крім чисел 2 і 5, є інші прості множники, то такий дріб перетворюється у нескінчений десятковий дріб. Щоб перевести чистий періодичний десятковий дріб потрібно чисельнику записати всі цифри, що стоять у періоді, а в знаменнику стільки дев’яток скільки цифр у періоді. 0,(12)= 11. Пряма пропорційність. Застосування до розвязування задач у початковій школі. Функція виду у=kx, k≠0. 1) Д=(-∞;∞) 2)Е=(-∞;∞) 3) При k>0 зростає; k<0 спадає; 4)не періодична 5)х=0, у=0 (0;0)-єдина точка перетину з осями; 6) f(-x)=k(-x)=-kx=-f(x)-ф-ія непарна, це означає, що графік буде симетричний відносно початку координат. Прямопропорційна залежність між двома величинами означає, що у скільки разів збільшується(зменшується) одна величина, то в стільки ж разів збільшується(зменшується) інша величина. Пр.: 3 кг цукерок коштують 70 грн. скільки будуть коштувати 6 кг цукерок? 3кг-70 грн 6кг -? грн 1)6:3=2(рази)-у стільки разів збільшилася маса цукерок; 2) 70*2=140(грн)-вартість 6 кг;
12. Перетворення звичайних дробів у десяткові. Умова, при якій звичайний дріб перетворюється в скінчений десятковий. Щоб перетворити звичайний дріб у десятковий, достатньо його чисельник поділити на знаменник. Якщо при діленні чисельника на знаменник матимемо нескінченний дріб, у якого одна або кілька цифр повторюються в одній і тій же послідовності, то такий дріб називають періодичним. У таких випадках говорять про наближене перетворення звичайних дробів у десяткові. Чистий періодичний дріб — такий дріб, у якого період починається одразу після коми, мішаний — такий, у якому між комою і періодом є одна або кілька цифр, що не повторюються. Якщо в розкладі на прості множники знаменника звичайного дробу є лише числа 2 і 5, то такий дріб перетворюється у скінчений десятковий дріб. Якщо в розкладі на прості множники знаменника звичайного нескоротного дробу, крім чисел 2 і 5, є інші прості множники, то такий дріб перетворюється у нескінчений десятковий дріб. Щоб перевести чистий періодичний десятковий дріб потрібно чисельнику записати всі цифри, що стоять у періоді, а в знаменнику стільки дев’яток скільки цифр у періоді. 0,(12)= 13. Множина – це не означуване поняття, яке використовують в різних науках для опису сукупності певних об’єктів.У математиці вивчають множини чисел, геометричних фігур та інших об’єктів. Позначають множини великими літерами латинського алфавіту А,В,С… Елементи множин позначають малими літерами: а,в,с… Якщо множина не містить жодного елемента,назив порожньою множиною. Множини можна задавати переліком елементів або за допомогою характерестичної вл-сті.
X ∩ Y X ∩ Y ∩ Z
X \ Y 3) А ∩ (B 14. Основні види задач, що розвязуються в початковій школі. 1) Щоб знайти дріб від числа потрібно число помножити на даний дріб. 2) Щоб знайти число за його дробом(частиною) треба цю частину числа поділити на даний дріб. 3) Щоб знайти яку частину одне число становить від іншого треба число про яке запитується в задачі поділити на інше число дане в умові. 3 типи задач на відсотки: 1) знаходження відсотка від числа; 2) знаходження числа за його відсотком; 3) знаходження відсоткового відношення двох чисел. Дійсні числа Кожне раціональне число можна подати у вигляді десяткового скінченного або нескінченного періодичного дробу. Наприклад: 4/5 = 0,8; 5/33 = 0,151515... =0,(15). І навпаки: кожному нескінченному періодичному дробу відповідає раціональне число. Але є числа, які не можна подати у вигляді скінченного або періодичного дробу. Означення. Число, яке подається у вигляді нескінченного неперіодичного дробу, називається ірраціональним числом. √2 — ірраціональне число. Проте ірраціональні числа утворюються не лише в результаті добування кореня. Наприклад, при порівнянні відрізка, узятого за одиницю, з будь-яким несумірним з ним відрізком дістаємо ірраціональне число. Несумірними відрізками є, скажімо, довжина будь-якого кола та його діаметр. Відношення довжини кола до діаметра дорівнює π= 3,1415926.... Означення. Множина раціональних чисел разом із множиною ірраціональних чисел утворюють множину дійсних чисел. Дійсні числа, як і раціональні, можна зображати на числовій осі. Нехай дано числову вісь із початковою точкою О та одиничним відрізком ОА (рис. 3). Зобразимо на цій осі точку, що відповідає ірраціональному числу V2. Для цього на відрізку ОА побудуємо квадрат та його діагональ ОС = V2. Накреслимо коло радіусом ОС. Тоді точка К перетину дуги кола з віссю Ох відповідатиме числу Кожному дійсному числу відповідає єдина точка на числовій осі, та навпаки. Множину дійсних чисел зазвичай позначають буквою R; використовують також символічний запис (−∞;+∞). Зауважимо, що пряма лінія, на якій вказані початок відліку, масштаб і напрямок, називається числовою віссю. Між множиною точок числової осі і множиною всіх дій-сних чисел існує взаємно однозначна відповідність. Це озна-чає, що кожна точка числової осі відображає одне дійсне чис-ло, і навпаки, кожне число являється координатою конкретної однієї точки числової осі. Дійсні числа зображують точками прямої. А саме, на деякій горизонтальній прямій, виберімо додатний напрям (зліва направо), початок відліку — точку O й одиницю масштабу. Точці M1, що лежить на прямій справа від точки O, зіставимо число x1=ӏOM1ӏ = — довжину відрізка OM1; точці M2, що лежить на прямій зліва від точки O,— число x2=-ӏ M2Oӏ < 0; точці O — число 0. Означення 2.1. Число x, що відповідає точці M, звуть координатою точки M, а пряму з описаною відповідністю звуть числовою прямою. Числова пряма дозволяє ілюструвати розташування дійсних чисел. Алгоритм Евкліда Нехай а і в нерівні нулю одночасно, причому а>в: 1)ділимо число а на число в; знаходимо неповну частку і остачу. 2)ділимо число в, отримуємо неповну частку і остачу. 3)ділимов на q. Продовжуємо цей процес до того часу доки не отримаємо в остачі 0. Тоді НСД чисел а і в дорівнює останній відмінній від нуля остачі в алгоритмі Евкліда.
Алгоритм знаходження НСК двох чисел 1.Розкласти числа на прості множники. 2.Записати всі множники з першого числа, а з другого виписати ті яких немає в першому. 3.Знаходимо добуток цих чисел. Якщо одне з двох натур. Чисел ділиться на друге число, то більше з цих 2 чисел є НСК. Якщо 2 числа є взаємопростими, то найменше спільне кратне дорівнює їх добуток. 4. Властивості множення та ділення додатних раціональних чисел. Будь-яке від’ємне число менше нуля і будь-якого додатного числа. Нуль менше будь-якого додатного числа. Наприклад: -5<0; -5<1; 0<10. Ділення додатних і від’ємних чисел 5. Кон’юнкція та диз’юнкція двох предикатів. Множина істинності кон’юнкції та диз’юнкції двох предикатів. Предикатом називається висловлювання з змінною, яке перетворюється в істинне або хибне висловлення при підстановці замість змінної конкретного значення. «х>5»-предикат, «6>5»-істинне, «3>5»-хибне. Множиною істинності предикату А(х) наз. множина значень змінної при яких предикат перетворюється в істинне висловлювання. ТА(х)≤х пр: А(х): Кон’юкцію двох предикатів А(х) і В(х) визначених на множині Х називається предикат виду А(х)˄ В(х), який перетворюється в істинне висловлення тоді, коли кожен з предикатів перетвориться в істинне висловлення. Множиною істинності предикатів буде переріз множин ТА(Х)˄В(Х) = ТА(Х)∩ТВ(Х) Прикладом кон’юкції двох предикатів є с-ма рівнянь або нерівностей Диз’юнкцією двох предикатів А(х) і В(х) називається предикат виду А(х)˅В(х), який перетворюється в істинне висловлення при тих значеннях змінних при яких хоча б один з предикатів стає істинним. Прикладом диз’юнкції предикатів є сукупність нерівностей Очевидно, що множину істинності кон’юкції та диз’юкції двох предикатів знаходять за формулами: ТА(Х)˄В(Х) = ТА(Х)∩ТВ(Х) ТА(Х)˄В(Х) = ТА(Х) 6. Ознаки подільності на складені числа (6,12,18) Ознака подільності на 6 Число ділиться на 6 тоді і тільки тоді, коли воно ділиться і на 2, і на 3, тобто якщо воно парне і сума його цифр ділиться на 3. Нариклад: 462, 3456, 24642 — діляться на 6, так як вони діляться одночасно і на 2, і на 3; 861, 3458, 34681 — не діляться на 6, так як 861 не ділиться на 2, 3458 не ділиться на 3, 34681 не ділиться на 2. Ознака подільності на 12. Для того щоб число х ділилося на 12, необхідно і достатньо, щоб воно ділилося на 3 і 4. Ознака подільності на 18. Для того щоб число х ділилося на 18, необхідно і достатньо, щоб воно ділилося на 2 і 9. 7. Розклад числа на прості множники. Основна теорема арифметики. Означення. Розкладом натурального числа n на прості множники (факторизацією числа) називається представлення його у вигляді n = Задача перевірки числа на простоту є простішою за задачу факторизації. Тому перед розкладанням числа на прості множники слід перевірити число на простоту. Означення. Розбиттям числа називається задача представлення натурального числа n у вигляді n = a * b, де a, b – натуральні числа, більші за 1 (не обов’язково прості). Метод Ферма Нехай n – складене число, яке не є степенем простого числа. Метод Ферма намагається знати такі натуральні x та y, що n = x2 – y2. Після чого дільниками числа n будуть a = x – y та b = x + y: n = a * b = (x – y)(x + y). Якщо припустити що n = a * b, то в якості x та y (таких що n = x2 – y2) можна обрати Тоді x = (13 + 11) / 2 = 12, y = (13 – 11) / 2 = 1. Перевірка: x2 – y2 = 122 – 11 = 143 = n. Теорема. Якщо n = x2 – y2, то < x < (n + 1) / 2. Доведення. З рівності n = x2 – y2 випливає, що n < x2, тобто < x. Оскільки a = n / b, то. Максимальне значення x досягається при мінімальному b, тобто при b = 1. Звідси x = <. Отже для пошуку представлення n = x2 – y2 слід перебрати всі можливі значення x із проміжку [, (n + 1) / 2], перевіряючи при цьому чи є вираз x2 - n повним квадратом. Приклад. Розкласти на множники n = 391 методом Ферма. = 19. 202 – 391 = 9 = 32. Маємо рівність: 391 = 202 – 32. Звідси 391 = (20 – 3)(20 + 3) = 17 * 23. Основна теорема арифметики стверджує, що будь-яке натуральне число більше одиниці може бути представлене у вигляді добутку простих чисел і таке представлення є єдиним з точністю до порядку множників. Для знаходження розкладу натурального числа на прості множники послідовно застосовується операція ділення числа на прості числа починаючи з найменшого. Причому, перехід до наступного більшого простого числа виконується тільки при неможливості цілого ділення на менше. Так, наприклад, можна отримати наступні розклади чисел 420 та 1200: Згідно з основною теоремою арифметики стверджується, що ці представлення є унікальними для кожного числа, тобто не існує розкладів з іншим набором чисел або іншою кількістю однакових множників. Відрізнятися може лише порядок множників, але, внаслідок комутативності та асоціативності множення, всі такі розклади є еквівалентними. Таким чином, теоремою стверджується, що не існує таких чисел, які можна було б розкласти на прості множники різними способами. 8. Відношення логічного слідування рівносильності на множині предикатів. Необхідні і достатні умови. Логічне слідування А(х) то В(х) означає, що з істинності А(х) обов’язково випливає істинність В(х), тобто А(х) є достатньою умовою для В(х), а В(х) необхідно випливає з А(х). А(х) → В(х) х:4→х:2 «Для того, щоб число ділилося на 2, для нього достатньо, щоб воно ділилося на 4» «Для того, щоб число ділилося на 4, необхідно, щоб воно ділилося на 2» А(х) → В(х) «Для того, щоб прямокутник був квадратом необхідно, щоб він був прямокутником» «Для того, щоб квадрат був прямокутником достатньо, щоб він був квадратом» У цих випадках не буде істинною обернена імплікація В(х) ≠ А(х) Але є логічні слідування які виконуються в обидві сторони: А(х): «х:3» В(х): «сума цифр: 3» А(х) → В(х) – істинна Якщо число ділиться на 3, то й сума цифр ділиться на 3. В(х)→А(х) – істинна Якщо сума цифр діл на 3, то й число діл на 3. Отже, істинною є еквіваленція цих предикатів, це означає, що можна записати предикати А(х) ↔ В(х) «число діл на 3, тоді і тільки тоді, коли сума його цифр діл на 3» або «для того, щоб число діл на 3, необхідно і достатньо, що сума цифр діл на 3». Теорема 5. Предикати P(x) і Q(x) рівносильні тоді і тільки тоді, коли кожний з них є логічним наслідком іншого. Якщо предикати P(x) і Q(x), визначені на множині M, такі, що предикат Q(x) є логічним наслідком предиката P(x), то предикат Q(x) називається необхідною умовою для предиката P(x), а предикат P(x) – достатньою умовою для предиката Q(x). Необхідна умова може не бути достатньою, а достатня – необхідною. Якщо з предиката P(x) логічно випливає предикат Q(x) і з предиката Q(x) логічно випливає предикат P(x), тобто вони рівносильні, то предикат Q(x) називається необхідною і достатньою умовою для предиката P(x), а предикат P(x) – необхідною і достатньою умовою для предиката Q(x). 9. Обернена пропорційність. Застосування до розв’язування задач в початковій школі. Функція виду у= Обернено пропорційна залежність між двома величинами означає що із збільшенням (зменшенням) однієї величина друга зменшується (збільшується) у стільки ж разів. Пр: 3 друкарки виконали роботу за 4 год. За скільки годин виконають цю ж роботу 6 друкарок? Чим більше друкарок, тим швидше вони виконають роботу. Це означає, що між кількістю робочої сили і часом існує обернено пропорційна залежність. 3 др – 4 год 6 др -? год 1) 6:3=2(р)-у стільки раз збільшилося друкарок; 2) 4:2=2(год)- для 6 друкарок. Обернено пропорційні величини є такі: 1)к-сть робочої сили і затрачений час; 2)швидкість руху і затрата часу; 3)ціна і к-сть товару на ті самі гроші; 10. Нескінченні періодичні десяткові дроби. Умова, при якій звичайний дріб перетворюється в періодичний. Щоб перетворити звичайний дріб у десятковий, достатньо його чисельник поділити на знаменник. Якщо при діленні чисельника на знаменник матимемо нескінченний дріб, у якого одна або кілька цифр повторюються в одній і тій же послідовності, то такий дріб називають періодичним. У таких випадках говорять про наближене перетворення звичайних дробів у десяткові. Чистий періодичний дріб — такий дріб, у якого період починається одразу після коми, мішаний — такий, у якому між комою і періодом є одна або кілька цифр, що не повторюються. Якщо в розкладі на прості множники знаменника звичайного дробу є лише числа 2 і 5, то такий дріб перетворюється у скінчений десятковий дріб. Нескінченний періодичний десятковий дріб – десятковий дріб, у якому нескінченно повторюється певна група цифр. Мінімальна група цифр, яка повторюється, називається періодом. Період записується в круглих дужках. Якщо в розкладі на прості множники знаменника звичайного нескоротного дробу, крім чисел 2 і 5, є інші прості множники, то такий дріб перетворюється у нескінчений десятковий дріб. Щоб перевести чистий періодичний десятковий дріб потрібно чисельнику записати всі цифри, що стоять у періоді, а в знаменнику стільки дев’яток скільки цифр у періоді. 0,(12)= 11. Пряма пропорційність. Застосування до розвязування задач у початковій школі. Функція виду у=kx, k≠0. 1) Д=(-∞;∞) 2)Е=(-∞;∞) 3) При k>0 зростає; k<0 спадає; 4)не періодична 5)х=0, у=0 (0;0)-єдина точка перетину з осями; 6) f(-x)=k(-x)=-kx=-f(x)-ф-ія непарна, це означає, що графік буде симетричний відносно початку координат. Прямопропорційна залежність між двома величинами означає, що у скільки разів збільшується(зменшується) одна величина, то в стільки ж разів збільшується(зменшується) інша величина. Пр.: 3 кг цукерок коштують 70 грн. скільки будуть коштувати 6 кг цукерок? 3кг-70 грн 6кг -? грн 1)6:3=2(рази)-у стільки разів збільшилася маса цукерок; 2) 70*2=140(грн)-вартість 6 кг;
12. Перетворення звичайних дробів у десяткові. Умова, при якій звичайний дріб перетворюється в скінчений десятковий. Щоб перетворити звичайний дріб у десятковий, достатньо його чисельник поділити на знаменник. Якщо при діленні чисельника на знаменник матимемо нескінченний дріб, у якого одна або кілька цифр повторюються в одній і тій же послідовності, то такий дріб називають періодичним. У таких випадках говорять про наближене перетворення звичайних дробів у десяткові. Чистий періодичний дріб — такий дріб, у якого період починається одразу після коми, мішаний — такий, у якому між комою і періодом є одна або кілька цифр, що не повторюються. Якщо в розкладі на прості множники знаменника звичайного дробу є лише числа 2 і 5, то такий дріб перетворюється у скінчений десятковий дріб. Якщо в розкладі на прості множники знаменника звичайного нескоротного дробу, крім чисел 2 і 5, є інші прості множники, то такий дріб перетворюється у нескінчений десятковий дріб. Щоб перевести чистий періодичний десятковий дріб потрібно чисельнику записати всі цифри, що стоять у періоді, а в знаменнику стільки дев’яток скільки цифр у періоді. 0,(12)= 13. Множина – це не означуване поняття, яке використовують в різних науках для опису сукупності певних об’єктів.У математиці вивчають множини чисел, геометричних фігур та інших об’єктів. Позначають множини великими літерами латинського алфавіту А,В,С… Елементи множин позначають малими літерами: а,в,с… Якщо множина не містить жодного елемента,назив порожньою множиною. Множини можна задавати переліком елементів або за допомогою характерестичної вл-сті.
X ∩ Y X ∩ Y ∩ Z |
||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 866; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.144.239 (0.011 с.) |


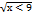 Обл визн х=[0;∞)…… ТА(х)=[0;81]
Обл визн х=[0;∞)…… ТА(х)=[0;81] (2;4]
(2;4] ТА˅В=(-∞;3)
ТА˅В=(-∞;3) 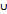 (5;∞)
(5;∞) ТВ(Х)
ТВ(Х) , де pi – взаємно прості числа, ki ≥1.
, де pi – взаємно прості числа, ki ≥1.
 Приклад. Виберемо n = 143 = 11 * 13.
Приклад. Виберемо n = 143 = 11 * 13.

 , k≠0. 1) Д=(-∞;0)
, k≠0. 1) Д=(-∞;0)  Щоб перевести мішаний періодичний дріб у звичайний потрібно в чисельнику дробу записати різницю чисел утворених таким чином (зменшуване дорівнює виписуємо всі цифри після коми, від’ємник дорівнює числу яке стоїть після коми до періоду), в знаменнику записуємо стільки дев’яток скільки цифр у періоді, і стільки 0 скільки цифр до періоду. 0,1(1,3)=
Щоб перевести мішаний періодичний дріб у звичайний потрібно в чисельнику дробу записати різницю чисел утворених таким чином (зменшуване дорівнює виписуємо всі цифри після коми, від’ємник дорівнює числу яке стоїть після коми до періоду), в знаменнику записуємо стільки дев’яток скільки цифр у періоді, і стільки 0 скільки цифр до періоду. 0,1(1,3)= 
 Поняття множини. Способи задання множин. Закони виконання операцій над множинами.. приклади на кругах Ейлера.
Поняття множини. Способи задання множин. Закони виконання операцій над множинами.. приклади на кругах Ейлера. Перерізом (перетином) двох довільних множин називається множина, елементами якої є ті і тільки ті елементи, що належать обом цим множинам. Графічно зображення перерізів двох і трьох множин за допомогою кругів Ейлера дано на мал. 1, де результати цих операцій заштриховано. Мал. 1.
Перерізом (перетином) двох довільних множин називається множина, елементами якої є ті і тільки ті елементи, що належать обом цим множинам. Графічно зображення перерізів двох і трьох множин за допомогою кругів Ейлера дано на мал. 1, де результати цих операцій заштриховано. Мал. 1. X або x? Y}.Графічне зображення об'єднання двох і трьох множин за допомогою кругів Ейлера дано на мал. 2, де результати цих операцій заштриховано.
X або x? Y}.Графічне зображення об'єднання двох і трьох множин за допомогою кругів Ейлера дано на мал. 2, де результати цих операцій заштриховано.


 В = А ∩ В;А∩В = А
В = А ∩ В;А∩В = А 


