Приклад схеми відновлення, заснованої на послідовності

Нехай n = 19 і S = <1,3,2,5,2,5>. Потім список відновлень, заснований на цій послідовності, є: R0 = <0,1,4,6,11,13,18>. Ця схема відновлення оптимальна для 8 пошкоджених вузлів. Малюнок нижче показує трикутник списку відновлення і усі різниці між номери в списку. Усі проміжні номери відмінні.

Мал. 6 Трикутник різниць.

Ми дивимося, що перші три збійні маршрути не перетинаються. (C1 ={1}; C2 ={4,3}; C3 ={6,5,2}) і в іншій частині збійних маршрутів знаходяться в найменшому l = 3 з унікальних значень. Отже, ця послідовність оптимальна аж до щонайменшої кількості пошкоджених вузлів. Жирні номери в трикутнику будують свого роду чотирикутник з непаралельними сторонами. Тому нові схеми сконструюванні таким чином що ми назвемо схеми чотирикутника з непаралельними сторонами.

 

Схеми відновлення чотирикутника з непаралельними сторонами проти схеми відновлення Голомбо

Перші маршрути l в схемі відновлення чотирикутника з непаралельними сторонами звані лінійкою Голом ба [1,3]. Схема відновлення Голомбо − регулярна схема відновлення. Для n вузлів в кластері ми будуємо список відновлень, користуючись відомою лінійкою Голомбо з сумою менше чи дорівнює n, і інша частина списку відновлень наповнена номерами, що залишилися, аж до n −1, наприклад для n = 12 ми маємо список <1,4,9,11,2,3,5,6,7,8,10>. Схеми відновлення чотирикутника з непаралельними сторонами засновані на лінійках Голомбо і заповнені номерами, які конструюють нові збійні маршрути. Схеми відновлення чотирикутника з непаралельними сторонами дають кращу оптимальність, ніж схеми Голомбо. У Таблиці 2 навантаження, що балансує чотирикутник з непаралельними сторонами, і схеми Голомбо порівняні.

Оптимальний навантаження, що балансує, гарантується для більшого ряду пошкоджених вузлів, якщо ми користуємося послідовностями чотирикутника з непаралельними сторонами, ніж послідовностями Голомбо, який має на увазі цей чотирикутник з непаралельними сторонами схеми залишаються близько до вектору MV для більшої кількості вимкнень. Наприклад, в цьому випадку з 127 комп'ютерів в кластері, послідовності чотирикутника з непаралельними сторонами гарантують оптимальну поведінку у випаду 21 вимкнень, поки лінійка Голомбо гарантує тільки оптимальність для 13 вимкнень. Покази таблиці 2 подають деякі приклади послідовностей. Для проміжних значень k ми використовуємо або меншу послідовність, або ми можемо просто знайти нову послідовність чотирикутника з непаралельними сторонами, що користується найближчим до лінійки Голомбо значенням. Наприклад, якщо число вузлів в кластері складає 15 потім, користуючись послідовністю з сумою 5 оптимальність гарантується для 3 вимкнень. Приклади чотирикутника з непаралельними сторонами послідовності представляються в Додатку.

 

Таб. 2 Порівняння послідовності чотирикутника з непаралельними сторонами і послідовності Голомбо.

Мал. 7 порівнює виконання схеми чотирикутника з непаралельними сторонами, з виконанням схеми, використовуючи лінійку Голомбо як функцію числа вузлів в кластері (n) аж до n = 1024. Виконання визначене, як число вимкнень, якими ми можемо управляти, поки все ще зберігається гарантія оптимального поширення навантаження, коли найнесприятливіша комбінація вимкненьи комп'ютерів є. Немає ніяких великих відмінностей між схемами для маленького n. Для більшого n поведінка схеми чотирикутника з непаралельними сторонами є куди краща, ніж схеми Голомбо, наприклад, для n = 100 схема чотирикутника з непаралельними сторонами гарантує оптимальну поведінку, коли 15 вузлів вимикається, при схемі Голомбо гарантується оптимальна поведінка, якщо 10 комп'ютерів вимикається. Більші кроки в чотирикутнику з непаралельними сторонами крива є, тому що k і l залежать один від одного, тобто (подивіться також Секцію 4.2).

Мал. 7 Представлення різниці між схемою чотирикутника і схемою Голомбо

Обговорення і укладення

У багатьох кластерних і розподілених системах, проектувальник повинен забезпечити схему відновлення, яка визначає, як робоче навантаження треба перерозподілити, коли один або більше комп'ютери вимикається. Мета − тримати навантаження, яке б порівну поширювалося як тільки можливо навіть, коли самі несприятливі комбінації комп'ютерів вимикаються.

Ми розглядаємо кластер з n ідентичними вузлами, які за нормальних умов виконують один процес кожен. Усі процеси виконують ту ж кількість роботи. Схеми відновлення, які гарантують оптимальне поширення навантаження в найгіршому випадку, коли k комп'ютери мають пошкодження. Схеми відновлення, представлені тут, можуть також бути використані в кластерах з рядом незалежних процесів на кожному комп'ютері. Це обговорюється в [11] і [12].

Викладення в цій статті, що ми подали нові схеми відновлення, схеми відновлення чотирикутника з непаралельними сторонами, де перша частина схеми заснована на відомій лінійці Голомбо, (тобто збійні маршрути не перетинаються) і в другій частині сконструйований шлях, де наступні збійні маршрути мають в найменших значеннях унікпльне l порівняно з попередніми збійними маршрутами. Схеми відновлення Голомбо представляються в [9]. Схеми відновлення чотирикутника з непаралельними сторонами гарантують краще виконання, ніж схеми Голомбо і є простими для обчислення. Для нечисленної кількості вузлів в кластері немає великої різниці між цими схемами. Але для більшого ряду вузлів поведінка схеми відновлення чотирикутника з непаралельними сторонами є куди краща, ніж схеми Голомбо, наприклад, для n = 201 схема чотирикутника з непаралельними сторонами гарантує оптимальний найгірший випадок поведінки для 28 вимкнень, поки схема Голомбо може тільки гарантувати це за 16 вимкнень.

Мета цієї статті − знайти хороші схеми відновлення, ще кращі, ніж вже відомі і які мають легко вичислити також відновлення для великого n. У попередній роботі [8] ми знайшли кращі можливі схеми відновлення для будь-якого числа пошкоджених вузлів в кластері. Щоб знайти, що така схема відновлення є такою ж в обчислювальному відношенні - комплексна задача. Через складності задачі ми тільки змогли подати оптимальну схему відновлення для максимум 21 вузла в кластері.

Схеми відновлення чотирикутника з непаралельними сторонами можуть бути негайно використані в комерційній кластерній системі, наприклад, визначаючи список в Сонячному Кластері, користуючись scconf командою. Результати можуть також бути використані, коли ряд зовнішніх систем, наприклад телекомунікаційні центри, що переключають, відправляють дані різним вузлам в розподіленій системі (або кластері де вузли мають індивідуальні мережеві адреси). У такому разі, списки відновлень є або здійснють як альтернативні місця призначення в зовнішніх системах, або в комунікації рівень протоколу, наприклад IP протокол [15].

Список літератури

1. Bloom, G. S., and Golomb, S. W., Applications of Numbered, Undirected Graphs, in

Proceedings of the IEEE, Vol. 65, No. 4, April, 1977, pp. 562−571C

2. Cristian, F., Understanding Fault Tolerant Distributed Systems, Journal of the

ACM, Vol 34, Issue 2, 1991

3. Dimitromanolakis, A., Analysis of the Golomb Ruler and the Sidon Set Problems,

and Determination of large, near−optimal Golomb Rulers, Dept. of Electronic and

Computer Engineering Technical University of Crete, June, 2002

4. Hewlett−Packard Company, TruCluster Server − Cluster Highly Available Applications,

Hewlett−Packard Company, September 2002

5. Hewlett−Packard, Managing MC / ServiceGuard, Hewlett−Packard, March 2002

6. IBM, HACMP, Concepts and Facilities Guide, IBM, July 2002

7. Kameda, H., Fathy, E.−Z. S., Ryu, I., Li, J., A performance Comparison of Dynamic

vs. Static Load Balancing Policies in a Mainframe − Personal Computer Network

Model, Information: an International Journal, Vol. 5, No. 4, December 2002, pp.

431−446

8. Klonowska, K., Lennerstad, H., Lundberg, L., Svahnberg, C., Optimal Recovery

Schemes in Fault Tolerant Distributed Computing, Acta Informatica, 41(6), 2005

9. Klonowska, K., Lundberg, L., and Lennerstad, H., Using Golomb Rulers for Optimal

Recovery Schemes in Fault Tolerant Distributed Computing, in Proceedings of

the 17th International Parallel & Distributed Processing Symposium IPDPS 2003,

Nice, France, April 2003

10.Klonowska, K., Lundberg, L., Lennerstad, H., Svahnberg, C., Using Modulo Rulers

for Optimal Recovery Schemes in Distributed Computing, in Proceedings of the 10th

International Symposium PRDC 2004, Papeete, Tahiti, French Polynesia, March

11.Lundberg, L., Haggander, D., Klonowska, K., and Svahnberg, C., Recovery

Schemes for High Availability and High Performance Distributed Real−Time Computing,

in Proceedings of the 17th International Parallel & Distributed Processing

Symposium IPDPS 2003, Nice, France, April 2003

12.Lundberg, L., and Svahnberg, C., Optimal Recovery Schemes for High−Availability

Cluster and Distributed Computing, Journal of Parallel and Distributed Computing

61(11), 2001, pp. 1680−1691

13.Krishna, C. M., Shin, K. G., Real−Time Systems, McGraw−Hill International Editions,

Computer Science Series, 1997, ISBN 0−07−114243−6

14.Microsoft Corporation, Server Clusters: Architecture Overview for Windows Server

2003, Microsoft Corporation, March 2003

15.Pfister, G. F., In Search of Clusters, The Ongoing Battle in Lowly Parallel Computing,

Prentice Hall PTR, 1998, ISBN 0−13−899709−8

16.Soliday, S. W., Homaifar, A., Lebby, G. L., Genetic Algorithm Approach to the

Search for Golomb Rulers, in Proceedings of the International Conference on

Genetic Algorithms, Pittsburg, PA, USA, pp. 528−535, 1995

17.Sun Microsystems, Sun Cluster 3.0 Data Services Installation and Configuration

Guide, Sun Microsystems, 2000

Додаток

В таблиці 3 подані приклади послідовностей чотирикутника з непаралельними сторонами. Жирні номери відмічені від Оптимальних Лінійок Голомбо.

 

Таб 3 Приклади послідовностей чотирикутника з непаралельними сторонами

Сума послідовності	Приклади послідовності чотирикутника з непаралельними стороними
	1,2,2
	1,3,2,1,3
	1,3,5,2,6,6,6,3,3,6
	1,3,6,2,5,13,1,9,2,3,8,5,6,3,6
	1,3,6,8,5,2,20,6,5,1,10,12,2,4,3,5,11,5,10,1,7
	1,3,5,6,7,10,2,24,3,11,2,20,2,2,8,6,2,19,2,6,6,2,13,10,2,14,6,7
	1,4,7,13,2,8,6,3,28,14,3,1,17,3,18,10,2,7,9,3,18,9,7,9,3,9,18,3,8,8,4,13,2,14,3,18
	1,5,4,13,3,8,7,12,2,36,1,5,4,13,3,8,7,12,2,36,1,5,4,13,3,8,7,12,2,36,1,5,4,13,3,8,7, 12,2,36,1,5,4,13,3
	1,3,9,15,5,14,7,10,6,2,40,22,8,3,19,15,7,4,26,3,6,3,12,26,2,1,10,14,11,10,10,11,18,2,4,14,17,4,9,15,20,1,10,6,7,15,23,8,8,15,1,21,1,10,2
	2,4,18,5,11,3,12,13,7,1,9,48,2,4,18,5,11,3,12,13,7,1,9,48,2,4,18,5,11,3,12,13,7,1,9,4,8,2,4,18,5,11,3,12,13,7,1,9,48,2,4,18,5,11,3,12,13,7,1,9,48,2,4,18,5,11,3
	2,3,20,12,6,16,11,15,4,9,1,7,69,2,24,5,19,1,24,9,31,2,7,1,16,18,16,5,16,3,30,9,7,1,1,4,44,3,10,17,7,11,6,12,13,6,21,21,1,28,1,20,4,17,7,1,5,19,18,16,5,8,13,30,10,6,26, 10,11,9,16,29,1,10,7,25,2,19,7
	4,2,14,15,17,7,18,1,8,3,10,23,5,56,4,2,14,15,17,7,18,1,8,3,10,23,5,56,4,2,14,15,17,7,18,1,8,3,10,23,5,56,4,2,14,15,17,7,18,1,8,3,10,23,5,56,4,2,14,15,17,7,18,1,8,3,10,23,5,56,4,2,14,15,17,7,18,1,8,3,10,23,5,56,4,2,14,15,17,7,18
	4,16,10,27,2,3,14,24,11,12,13,8,1,6,95,3,45,5,13,18,18,18,17,19,6,13,6,15,31,4,13,1,5,2,23,34,10,7,14,12,18,10,6,28,11,6,14,33,20,2,9,12,22,9,25,9,1,5,35,15,8,20,19,1,1,6,21,16,11,31,9,6,19,12,2,30,17,15,23,2,3,14,14,9,8,29,1,17,32,8,2,33,5,23,13,9,6, 21,18,22,8,23,5,14,18,7,22

 

 

Стаття VI

Оптимальні Схеми Відновлення в Розподілених Обчисленнях Толерпнтних до Помилок

 

 

Kamilla Klonowska, Lars Lundberg, Hakan Lennerstad, Charlie Svahnberg

Acta Informatica, 41(6), 2005

 

Резюме

Кластери і розподілені системи дозволяють толерантність до помилок і високу продуктивність через спільне використання навантаження. Коли усі комп'ютери працюють, ми хотіли б розподілити навантаження порівну серед комп'ютерів. Коли один або більше комп'ютерів ламаються навантаження на цих комп'ютерах має бути перерозподілене на інші комп'ютери в кластері. Перерозподіл визначає схема відновлення. Схема відновлення управляється послідовністю модулів цілих чисел n. Кожна послідовність гарантує мінімальне навантаження комп'ютера, який має максимальне навантаження навіть, коли самі несприятливі комбінації комп'ютерів вимкнені. Ми обчислюємо кращі з можливих схем відновлення для будь-якого числа пошкоджених комп'ютерів повним перебором, перевіряючи уникаємо математичного переформулювання. Пошук проте має високу складність. Оптимальні послідовності, а отже оптимальна межа передачі, представляються для максимум двадцяти одного комп'ютера у розподіленій системі або кластері.

Ключові слова: розподілені системи, схема відновлення, відмова, баланс за навантаженням, ціле число

Послідовності.

Вступ

Один шлях отримання високої придатності і толерантність до помилки − виконувати додаток на кластерній або розподіленій системі. Є головний комп'ютер, який виконує додаток за нормальних умов і вторинний комп'ютер, який приймає задачу, коли головний комп'ютер вимкнений. Можливо, також є третій комп'ютер, який приймає задачу, коли головний і вторинний комп'ютери − вимкнені, і так далі. Інша перевага з використанні розподілених систем або кластерів, окрім толерантності до помилки, − спільне використання навантаження між комп'ютерами. Коли усі комп'ютери працюють, ми хотіли б розподілити навантаження порівну. Навантаження на деяких комп'ютерах буде, проте, зростати коли один або більше комп'ютерів вимикаються, але і за цих умов, поширення навантаження на комп'ютерах, що залишилися можна розподілити порівну. Поширення навантаження, коли комп'ютер вимкнений вирішене списками відновлень процесів виконуваних на помилковому комп'ютері. Сукупність усіх списків відновлень називається схемою відновлення. Отже поширення навантаження повністю визначає схема відновлення для будь-якої кількості комп'ютерів, які вимикаються. Задача виявлення оптимальної (або навіть кращої) схеми відновлення була вивчена в [16,17]. У поданій статті ми обчислюємо кращу з можливих схем відновлення для усього n. Найбільше кластерних виконувачів підтримують цей вид оновлення при помилках, наприклад nodelist в Sun Cluster [17], список пріорітетів MC/ServiceGuard (HP) [5], каскадна група в HACMP (IBM) [6], і лист представлення в Windows Server 2003 clusters (Microsoft, earlier called MSCS) [22].

У [5] толерантності до помилки для розподіленого обчислення мова йдеться від загальної точки зору. Балансування завантаження і придатність особливо важливі в розподілених системах толерантних до помилок де передбачити важко, на якому комп'ютері процеси треба виконувати. Ця задача NP−повна для великої кількості комп'ютерів [30]. Крішна і Шін визначають толерантність до помилки як здатність системи миттєво відповісти до несподіваної помилки технічного забезпечення або програми [18]. Тому, багато толерантних до помилок комп’ютерних систем, віддзеркалюють усі дії, наприклад на кожній дії виконується дві або більше подвійні системи в тому сенсі, що, якщо одина робить, інша може прийняти її роботу. Ця техніка також використана в кластерах [23].

Один може управляти цією задачею динамічно, де трансферні рішення не залежать від фактичного стану системи. Задача з динамічною політикою є швидше непередбачувана. Інакше необхідно користуватися статичною політикою, на якій загалом заснована інформація поведінки системи. Тут, трансферне рішення є незалежне від поточного стану системи. Це робить їх менш комплексними і більш передбачуваний, ніж динамічна політика [15]. Окрім апаратних відмов, переривчасті відмови можуть відбуватися із-за програмного забезпечення події. У [29] "дворівневі" схеми відновлення представлені і оцінені. Схема Відновлення була здійснена на кластері. Автори оцінюють дію час очікування контрольно-перепускного пункту на виконанні схеми відновлення. Для операційно-орієнтованих систем, в [7], Ґеленб запропонував "багаторазовий check підхід, ", тобто подібний до багато-горизонтальної схеми відновлення яка була присутня в [29]. Математична модель операційно-орієнтованої системи під переривчастими відмовами пропонується в [9]. Тут система передбачається для дії в стандартній схемі відновлення зворотного перемотування контрольно-перепускного пункту. У [3] і [8] автори пропонують декілька алгоритмів, які можуть сформулювати відмови задач і знову почати невдалі задачі. Вони аналізують поведінку паралельних програм, представлених близько випадкової task−діаграми в мульти-процесорному середовищі. Проте, усі ці алгоритми діють динамічно.

Наші результати також дійсні, коли є системи n зовнішнього живлення даних всередині кластера, наприклад, один телекомунікаційний центр живлення даними в кожному з n комп'ютерів в кластері. Якщо комп'ютер зламаний, обмінний центр повинен послати його дані до деякого іншого комп'ютера в кластері; тобто, доводиться мати асоційований список відновлень з кожним обмінним центром. У першому порядку для несправності може альтернативно управляти рівень протоколу комунікації, наприклад IP протокол [24].

Багато кластерних виконувачів пропонують не лише щоб користувач визначив списки відновлень, що розглядаються тут але і динамічне навантаження, що балансує схеми, коли вузол вимкнений.

Проблемна область і формулювання представляються в Секціях 2 і 4. Наші попередні дослідження на цій задачі описується в Секції 3. У Секції 5 ми подали головні результати. Напруженість нижньої межі була присутньою в [16,17] розслідується в Секції 6. У тій же секції ми описуємо алгоритм виявлення оптимальних послідовностей. Укладення представляються в Секції 7.

 

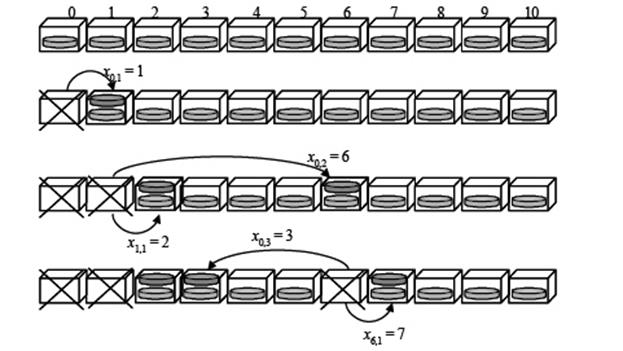
Проблемна область

У цій секції ми подали зразкову пояснюючу термінологію, використану в цій статті. У Додатку ми обговорюємо випадок, коли є ряд незалежних процесів на кожному комп'ютері. Проте, доти ми припускаємо, що робота, що виконується близько n комп'ютерами має бути переміщена як одна атомна одиниця. Це дуже загальний сценарій у тому числі випадки, коли:

• робота, що виконується комп'ютером, робиться від однієї зовнішньої системи;

• є одна мережева адреса для кожного комп'ютера і ми користуємося IP протоколом (або подібною

технікою);

• усю роботу, що виконується комп'ютером, робить один процес або група пов'язаних процесів, що є загальними місцевими ресурсаи і отже мають бути переміщені як одна одиниця.

Деякі комп'ютерні мережі, як наприклад гіперкуби [1,10], обмежують комунікації шляхів в системі, таким чином, що повідомлення від комп'ютера до комп'ютера B доведеться в деяких випадках послати через комп'ютер C (чи D,...). Проте, багато bus−based систем, наприклад системи, які користуються ethernet [13], використовують прямі комунікації між будь-якими парами вузлів в кластері [26]. Ми припускаємо, що можливо знову почати роботу на будь-якому комп'ютері в кластері (або переадресувати канал зв'язку в цьому випадку зовнішньої системи живлення даних до кластера). Ми вважаємо систему або кластер повністю сполученням з n ідентичних комп'ютерів. Впродовж нормальної дії є один процес на кожному комп'ютері. Робота є рівномірно розділена між цими n процесами. Кожен процес має список відновлень, який визначає у якому комп'ютері процес має бути знову початим, якщо поточний комп'ютер вимкнений. Якщо комп'ютер ламається, процес переміщається в наступний комп'ютер в списку, і так далі. Ми припускаємо, що процеси переміщаються назад, як тільки комп'ютер приходить знову. У найбільших кластерних системах це може задати користувач [12,27,28], тобто в деяких випадках один, можливо, не хоче автоматичного перерозподілу процесів, коли помилковий комп'ютер повертається знову.

Процес в комп'ютері i 0 ≤ i ≤ n – 1, переміщається в комп'ютер x _{i , 1}, якщо комп'ютер i вимкнений. Якщо комп'ютер x _{i , 1} також вимкнений, або ламається перед тим, як комп'ютер i вимкнеться, той же процес переміщається в комп'ютер x _{i , 2}, і так далі. Загалом, якщо усі комп'ютери xi, 1, xi, 2, …, xi, j – 1 вимикаються, і комп'ютер xi, j працює, процес, який був спочатку в комп'ютері i знаходиться в показах комп'ютера xi, j. Мал.1 приклад перерозподілу процеса від комп'ютера нуль. Комп'ютери нуль, один і шість вимикаються. Тому просес від комп'ютера нуль на комп'ютері x _0,3 = 3.

Мал. 1 Трансфер процесу від комп’ютера 0

Щоб уникнути напряму процесу до комп'ютера, який ми знаємо, зламався, усі входи в список відновлення мають бути чітким.

Ми головним чином розглядаємо регулярні схеми відновлення. Потім усі списки мають ту ж структуру задану вектором R, як зазначено нижче:

0: < R 1, R 2, …, Rn – 1>

1:< R 1 + 1, R 2 + 1,…, Rn – 1 + 1>

…

n −1: < R 1 + n – 1, R 2 + n – 1,…, Rn – 1 + n – 1> − де всі числа обчислені mod n.

Ми позначаємо перший комп'ютер R 0 = 0 і усі комп'ютери через x 0, i, Ri для i = 1, …, n – 1. Відмітьте, що процес спочатку в комп'ютері нуль знаходиться в комп'ютері Rj після j вимкнень.

Наприклад, для n = 6 ми маємо наступні регулярні схеми відновлення дані вектором R = <0,1,3, 5,4, 2>:

0: 1, 3, 5, 4, 2

1: 2, 4, 0, 5, 3

2: 3, 5, 1, 0, 4

3: 4, 0, 2, 1, 5

4: 5, 1, 3, 2, 0

5: 0, 2, 4, 3, 1.

Кількість регулярних схем відновлення з довжиною n (n комп'ютерів) означає R(n). Там явно (n – 1)! відмінні такі послідовності з n комп'ютерами, так R (n) = (n – 1)!.

 

Попереднє дослідження

У попередній роботі ми подали алгоритми, які дають схеми відновлення оптимальні для ряду пошкоджених комп'ютерів. У [20] задачі виявлення схеми відновлення, яка може гарантувати оптимальний найгірший випадок поширення навантаження, коли більшість x комп'ютерів вимикаються. Схеми повинні мати так великий x як можливо. Ми представляємо і доводимо Log алгоритм, який будує схеми відновлення, які гарантують оптимальність, де найбільше log₂n комп'ютерів вимкнені. Тут оптимальні засоби, максимального числа процесів на тому ж комп'ютерів після k вимкнень − BV (k), де функція BV (k) забезпечує нижню межу для будь-якої схеми статичного відновлення. BV є визначенням, що зростає і містить точно k входи, це дорівнює k для усього j−того входу у вектор BV дорівнює . Отже BV (p) =<2,2,3,3,3,4,4,4,4,5,5,5,5,5,6, …>

У [16] ми подали два інші алгоритми, Ощадливий алгоритм і схему Голомбо. Ці алгоритми роблять схеми відновлення, які дають кращу оптимальність, ніж Log алгоритм (тобто краще балансування навантаження). Ощадливий алгоритм заснований на математичній задачі виявлення послідовності додатніх цілих чисел такий, що уся сума послідовностей унікальна і мінімальна. Легко вичислити Ощадливий алгоритм навіть для великий n. Список відновлень для комп'ютера номер нуль складається з двох частин. Перша частина − послідовність від Ощадливого алгоритму, і друга частина наповнена залишковими номерами. Інші списки отримують із самого початку складаючи список, який включаює модуль одного змісту. Схема відновлення схема, що складається з усіх списків відновлень.

Схема Голомбо − окремий випадок Ощадливого алгоритму. Ім'я цього алгоритму приходить від лінійки Голомбо [2,6]. Математичне формулювання було змінено в спостереженні за щонайдовшою послідовністю додатніх цілих чисел таких, що сума послідовності менша або дорівнює n і усіх сум включених послідовностей (послідовності довжини один) унікальні, де n − число комп'ютерів в кластері. Списки відновлень Голомбо формулюються як наприклад Ощадливих списків відновлень: для k комп'ютерів в кластері ми будуємо список відновлень для комп’ютера нуль, використовуючи відому Лінійку Голомбо з сумою менше або дорівнює k, і інша частина списку відновлень заповнена номерами, що залишилися, аж до k −1, наприклад для k= 12 ми маємо список <1,4,9,11,2,3,5,6,7,8,10>. Усі інші списки відновлень отримують із самого початку додаючи один в змісті модуля.

Схеми Голомбо дають оптимальність для більшого ряду вимкнених комп'ютерів, ніж Ощадлива схема. Проте, знахлдження (і доказ) оптимальних схем Голомбо стає показово важчим, оскільки число комп'ютерів (n) зростає [32,33]. Тому, для великого n ми можемо легко вичислити послідовність з чіткими частковими сумами з Ощадливого алгоритму, де ніякі послідовності Голомбо не відомі.

У [17] ми оптимізуємо задачу близько зважаючи на сценарій циклічного переходу: просес посланий назад або проходячи повз головний комп'ютер. Це відповідає новій математичній задачі виявлення щонайдовшої послідовності додатніх цілих чисел сума усіх послідовностей яких є унікальним модулем n. Це математичне формулювання комп'ютерної постановочної задачі дає нові потужніші схеми відновлення названі модульними схемами, це оптимально для більшого ряду пошкоджених комп'ютерів в оригінальній комп'ютерній постановочній задачі. Тобто ці результати представляють сучасний стан поля. Модульна схема відновлення формулюється як наприклад Ощадливої схеми відновлення і схеми відновлення Голомбо. Характеристики і обговорення деяких прикладів схем представляються в Секції 5.4.

 

Проблемне формулювання

У цій секції ми уперше визначаємо навантаження на найбільш сильно занавантажеий комп'ютер після p вимкнень. Потім ми спостерігаємо за оптимальними схемами відновлення, вибираючи схеми які мінімізують це навантаження.