
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Від чотирьох копій в три нові програмиСодержание книги
Поиск на нашем сайте Спершу ми обговорюватимемо локальну проблему планування. Нехай програми Р Р’ і Р’’ будуть ідентичними програмами, за винятком того, що довжина кожної роботи в P ″ - подвоєна у відповідності до роботи в Р’, і довжина кожної Роботи Р рівна нулю. Розглянемо виконання Р’’, де розміщення А - оптимальний локальний графік. Нехай Q буде програмою, де ми об'єднали усі процеси, що виконуються на тому ж процесорі в одному процесі. рис. 8 показує, як P 2″і P 3″ об'єднані в процес Q 2″. Нехай Q ′буде програмою, яка ідентична до Q ″ з винятком того, що довжина кожного Робочого часу ділиться на два. Нехай Q буде програмою, яка ідентична до Q ″і за винятком того, що робочий час - нульовий
Рис 8. Перетворення P” в Q” З теореми 2, ми знаємо, що 2 Ts (Q ′, A)≤ Ts (Q, A)+ Ts (Q ″, A). І ми використовуємо таке ж розміщення «А» для обох P ″ і Q ″Проте, відколи є менше процесів в Q ″ми нехтуємо розміщенням неіснуючих процесів в Q ″. Це означає, що кожен процес в Q ″ розподіляється для власного процесора. Із визначення Q ″ ми знаємо що Ts (P ″, A) = Ts (Q ″, A). Від того як оптимального порядок, в якому процеси розподілені до того ж процесора (тобто оптимальний локальний графік), можливо, не є тим же для P ′ і P ″ ми знаємо що Ts (P ′, A)≤ Ts (Q ′, A). Роглянемо зараз програму R, так як число процесів в R рівне числу процесів в Р, і так як R виконує нульову Роботу (тобто R містить тільки синхронізації, подібні до Р). Число синхронізацій між процесами Ri і Rj в програмі R – подвійне значення синхронізацій між процесами Pi і Pj в програмі Р. Це означає, що завжди є ряд синхронізацій між будь-якою парою процесів в R. Всі синхронізації в R повинні виконуватися в порядку (Рис. 9). Ми знаємо, що завжди можливо сформувати таку послідовність яка є рядом синхронізацій між будь-якою парою процесів. Послідовне виконання синхронізацій очевидно представляє "найбільш погано працюючу» програму, і локальне планування не впливає на тривалість виконання послідовності програм. Отже ми знаємо, що 2 Ts (P, A)≤ Ts (R, A) і 2 Ts (Q, A)≤ Ts (R, A). Тому: 4 Ts (P ′, A)≤4 Ts (Q ′, A)≤2 Ts (Q, A)+ 2 Ts (Q ″, A)≤ Ts (R, A)+ 2 Ts (P ″, A).
Рис 9, Перетворення програми Р в програму R Ми довели наступне: Теорема 3: Для будь-якого розміщення А: 4 Ts (P ′, A)≤ Ts (R, A)+ 2 Ts (P ″, A). Це означає, що довжина чотирьох копій P ′ користування розміщенням А є менша ніж відповідна сума довжин програми R і двох копій P ″ що використовують же розміщення А. Перетворення продовження змінює робочий час але не число синхронізацій. Отже перетворення продовження безпосередньо не зберігає міру деталізації. Проте, в порівнянні Теореми 3, обидві альтернативи мають ту ж деталізацію. Ми бачитимемо, що Теорема 3 грає важливу роль в наступній частині, де ми виокремимо програму в двох частинах. 4.4 Перетворення програм P в програму з «товстою» і «тонкою» частинами У цій секції ми описуємо, як перетворити м копій програми P ′ в програму з однією частиною, що складається тільки з сигналів синхронізації (тонка частина), і інша частина, що складається з усієї обробки (товста частина). Перейміть на себе довільну програму P ′. Спершу ми створюємо м копій P ′, де m = 2х для деякого (крупно) цілого числа (з Леми 1 ми знаємо, що коефіцієнт Ts (P, k, t)/Td (P, q) не змінюється)., Ми комбінуємо «м» копій в групах чотири і перетворюємо кожногу групу до двох програм P ″ і однієї програми R. З теореми 3 ми знаємо що 4 Ts (P ′, A)≤ Ts (R, A)+ 2 Ts (P ″, A) для будь-якого розміщення А. перетворення закінчується з 2 x – 1 програмами P ″ і 2 x – 2 програмами R. Знову ми комбінуємо 2 x – 1 програми P ″у групах по чотири і використовуємо ту ж техніку. Цього разу перетворення закінчується з 2 x – 2 програмами P ″ (порівнявши із подвійним виконанням до P ″) і 2 x – 3 програмами R, які ми додаємо попереднім 2 x – 2 програмам цього типу. Ми повторюємо це техніка до там – дві дуже «товсті» програми з усім виконанням і з синхронізації в товстій частині. Ми користуватимемося цим фактом в наступній частині. міра деталізації z зберігає перетворення. Перетворення для m = 8 ілюструється в рис. 10. Програма S ″ представляє програму що складається з двох частин: тонка (трьох програм R) і товста (двох програм P'''). Це перетворення дозволяє оптимізувати статичний розподіл часу завершення тільки для зростання, тобто. mTs (P ′, k, t) Ts (S, k, t)≤ T = s (S ′, k, t)≤ Ts (S ″, k, t) Але в динамічному розподілі, де вартість синхронізації дорівнює нулю, час завершення справжній впродовж перетворення. Тому, Від цього покажчика і далі, ми обговорюватимемо тонку частину програм P ″ (програмні секції з тільки синхронізацією) і окремо товста частина програми (програмна секція з тривалістю виконання). Товста частина У цій секції ми обговорюємо товсту частину, тобто програмні секції, де ми можемо нехтувати часом синхронізації. Ми, можемо, припустити, що t = 0, коли ми працюємо з товстою частиною. Результат цієї секції - формула функції g (A,n,k,q) де А - розміщення процесів до процесорів. Ця функція - один з двох ключових компонентів нам необхідних для того, щоб досягти кінцевої мету: H (n, k, q, t, z). 5.1 Перетворення P в Q Розглянемо, довільну паралельну програму Р з n обробками і мультипроцесорною системою із q процесорами і динамічним розподілом. У цьому перетворенні ми додаємо нові синхронізації до Р, таким чином Td (P, q), що не зростає. Ts (P, k, t) проте може, зростати через нові синхронізації. Нові синхронізації гарантують Рис 10, Трансформація від м=8 копій Р в нову програму із Товс і Тон частинами. що, незалежно від того, як процеси розподілені і планується, там не може бути більше чим q одночасно активні процеси. Тривалість виконання, що користується оптимальним динамічним розподілом, розділена в м однаково розмірні відрізки часу таким чином, що обробляють синхронізації, які завжди відбувається відрізок часу. Для того, щоб отримати нову програму, ми додаємо нові синхронізації у кінці кожного відрізку часу. Ці синхронізації гарантують, що немає обробки, зробленої в слот r 1 < r ≤ m, користуючись оптимальним динамічним розподілом, може бути зроблений за винятком усієї обробки в r – 1слот був завершений. рис. 11 показує, як програму Р перетворено в нову програму Q.
Рис 11, Перетворення програми Р в Q
Синхронізації в Q формують супер набір синхронізацій в P, тобто Ts (P, k, t)≤ Ts (Q, k, t). Тому,. Ми потім мотивуємо, що межа дійсна під цим спрощенням. Означає користь цього аргументу Ts, t (Q, k, t)часом завершення, коли кожна нова синхронізація має час завершення t. Отже відносна вага нових синхронізацій зменшуються x, отже Аргументом справжнього перетворення, ми маємо Цим аргументом ми, можемо, нехтувати часом завершення для появи нової синхронізації в цьому перетворенні. Це дозволяє нам імпортувати результати із [10]. Якщо довільна програма в запуску перетворень - повна програма, синхронізація не додається. Отже, повні програми виконують цю межу. Для того, щоб спростити наступне обговорення, ми представляємо еквівалентне представлення Q так зване векторне представлення (Рис 11). У цьому представленні, кожен процес представляється як двійковий вектор м довжини, де м - число часу слотів в Q. Це означає, що паралельна програма представляється як бінарні вектори n набору. У деяких випадках ми задовольняємо ці вектори як одну двійкову матрицю m × n, де кожен стовпець відповідає вектору і кожному ряду до відрізку часу. Надалі ми переймаємо на себе довжину слота одиничного часу, тобто Td (Q, q) = m., Проте Ts (Q, k, t)≥ m, оскільки, якщо число активних процесів перевищує число процесорів на деякому процесорі впродовж деякого відрізку часу, виконання цього відрізку часу буде взято більш ніж один модуль. Ми обробляємо зараз програми як двійкову матрицю. Кожен стовпець в матриці представляє один процес, і ряди є незалежно один від одного. 5.2 Перетворення Q в Q' Перетворюючи Q в нову програму Q', ми починаємо із створення n! копій Q. Вектори в кожній копії змінені порядок таким чином, що кожна копія відповідає одна з n!можливих перестановок n векторів. Векторний номер v (1≤ v ≤ n) в копії чисел c (1 ≤ c ≤ n!) складений з векторів номер v в копії, отже формуючи нову програму Q ′з n векторами довжини n! помножену n на тривалість виконання від слота 1+(c – 1) m до (1≤ c ≤ n!) см не може бути менш ніж Ts (Q, k, t)., Тобто Ts (Q ′, k, t)не може бути менш ніж n! Ts (Q, k, t). Починаючи з Td (Q ′, q) = n! m ми знаємо що N вектори в Q ′можуть розглядатися як стовпці в матриці. Пере упорядковування в ряди в цій матричні викликає Ts (Q ′, k, t)ні, Td (Q ′, q). ряди в Q ′ можуть бути пере упорядковані в (n/q) однаково розмірних групах послідовних рядів, де усі ряди в така ж група ідентичні. Кожна група відповідає одній з можливих перестановок q ті і n – q нулі. Очевидно, на діапазон Надалі ми посилатимемося на цю програму, що згортається, як Q ′. Рис. 12 показує, як всередину двох повних програм (Q 1і Q2) перетворюється програма Q. Важливо відмітити, що усі повні програми призводять до тієї ж програми Q. Тому, ми знаємо,
|
||
|
Последнее изменение этой страницы: 2016-06-22; просмотров: 359; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.41 (0.007 с.) |



 програми R. Частина, що складається з двох дуже товстих програм, з велокою кількістью виконань і дуже слабкою синхронізацією, так званою товстою частиною. 2 x – 1 – 1 Копії R, що містять (майже усю) синхронізацію, зоветься тонкою частиною. Відмітьте, що вибираючи досить великий m = 2 x, ми можемо нехтувати часом завершення
програми R. Частина, що складається з двох дуже товстих програм, з велокою кількістью виконань і дуже слабкою синхронізацією, так званою товстою частиною. 2 x – 1 – 1 Копії R, що містять (майже усю) синхронізацію, зоветься тонкою частиною. Відмітьте, що вибираючи досить великий m = 2 x, ми можемо нехтувати часом завершення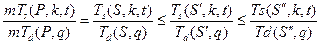 .
.


 .
. для усіх x. Отже
для усіх x. Отже  .
.
 не впливає факт що кожен ряд - дублює
не впливає факт що кожен ряд - дублює  часи. Це означає, що програма Q ′ може згортатися у програмі (n/q) з рядами, містячи можливі перестановки q і n – q нулями.
часи. Це означає, що програма Q ′ може згортатися у програмі (n/q) з рядами, містячи можливі перестановки q і n – q нулями. що. Ми зараз знайшли більш «погано працюючу» програму.
що. Ми зараз знайшли більш «погано працюючу» програму.


