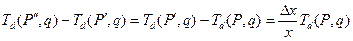Перетворення програми Р в нову програму що містить вузьку і широку частину.

 

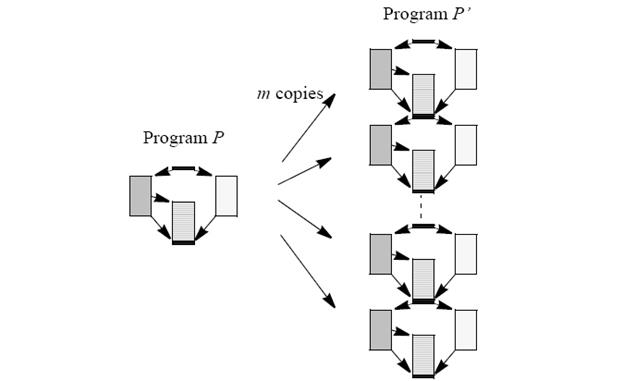
У цій секції ми покажемо техніку, яка дозволяє нам перетворювати програму у нові програми, що складається з двох частин, одна це виконання (також називається товста частина), а інша частина тільки синхронізація (тонку частину). У цій секції ми показали дві леми і три теореми, що доводять можливість таких перетворень

4.1 Програма Р’ як м-ідентична копія програми Р

У цьому перетворенні ми конструюємо програму Р’, створюючи м копій програми Р

Усе виконання в копії x має бути завершене перед тим, як копія x + 1 зможе початися. Це

не вимагає ніякої додаткової синхронізації, поки не буде необхідності в зв'язуванні процесів з добре визначеними точками початку і кінця (подивіться Мал. 4). У лемі 1 ми показуємо, що це перетворення не змінює коефіцієнт разів завершення з оптимальним статичним розподілом, порівнянним з оптимальним динамічним розподілом.

Лема 1: Діапазон часу завершення роботи при оптимальному часі завершення не розниться від переключення між програмами Р’ і Р

Доказ:, Маючи м (м > 1) копій програми Р, ми множимо обидві кількості

 

 

Рис. 4 показує перетворення програми в копіях м цієї програми позначається як Р’, Програма Р (ліва частина в малюнку) складається з виконання і синхронізаційних сигналів

Рис 4. Перетворення програми Р м копій Р

 

Пізніше ми перетворимо ці м копій в двох частинах: одна частина з синхронізаційні

сигнали тільки один з повним виконанням. Перед цим, ми показували інше перетворення, перетворення -продовження, де ми продовжуємо процеси.

Продовження процесів

Це перетворення істотне для спрощення у безлічі "більш погано працюючих" які ми називаємо «завершеними». Ми бачитимемо, що властивість опуклості перетворення (Теорема 1:) грає центральну роль.

Ми перетворюємо програму Р в Р’ продовженням процесів. Тобто, ми пропонуємо кожного разу доки x, x > 0, з кожного процесу в програмі Р таким чином Δ x, що Δ(x ⁄ x) - те ж для усіх процесів. Програма Р’

потім перетворена в Р’’ таким же чином. Тобто, після перетворення кожного разу коли блок x + Δ x продовжено на Δ x. Кожну Роботу(x) замінює Робота (x + Δ x) для Р’ і константа Роботи (x + 2Δ x) для Р’’

, де Δ(x ⁄ x).

Це перетворення не впливає на синхронізацію. В цьому випадку динамічного розподілу, коли вартість синхронізації дорівнює нулю після продовження, ми просто маємо:

.

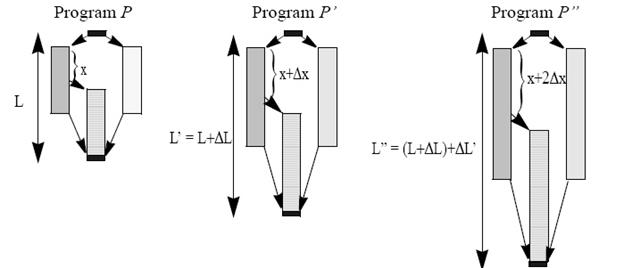
Ситуація для статичного розподілу відмінна від попередньої. Починаючи з вартості комунікації, яка в цьому випадку не нульова, відмінності після продовження не завжди зберігаються, тому що ми не продовжуємо синхронізацію. Мал. 5 демонструє перетворення. Для простоти зображення знаками ми позначаємо час Ts (P, A) статичного завершення замість Ts (P, A, k, t), і позначаємо довжину програми L minA = Ts (P, A). різницею між Р і Р’ позначаємо, як Δ L. Це означає, що довжина програми Р’ дорівнює L ′ = L + Δ L Програма Р’’ створюється так само, використовуючи те ж Δ x в Р’.

Різниця між Р’ і Р’’ ми позначаємо, як Δ L ’. Потім довжина програми Р’’ буде L ″ =(L + Δ L)+ Δ L ′.

Рис

 

Рис 5. Перетворення програми Р за допомогою пролонгації

 

Властивість опуклості, яка формулюється в Теоремі 2, витікає з Теореми 1 і заявляє, що Δ L ≤ Δ L ′. Ці теореми визначаються пізніше. Для того, щоб обговорювати ефект роздільного локального планування, ми розглянемо тільки один процес на процесор. Ми ослабимо це обмеження у кінці цього розділу.

Спершу ми визначаємо деяку термінологію:

Шляхом програми ми визначаємо підключену послідовність сегментів і синхронізації сигнали. Шлях починається завжди на початку програми. Довжиною шляху ми визначаємо час для усього виконання і сигналів синхронізації, які включаються у шлях. Найдовшим шляхом ми визначаємо шлях з максимальною довжиною. Критичним шляхом ми визначаємо щонайдовший шлях з мінімальним числом сигналів синхронізації. Отже коли ми маємо два щонайдовші шляхи, потім критичний шлях буде шляхом з менше стрілки. Для простоти ми використовуємо "стрілку" це скорочення для поняття «синхронізаційний синал»

Мал. 6 показує програму з чотирма процесами на чотирьох комп'ютерах, що містять чотири синхронізаційні сигнали. Права частина малюнка показує ієрархічну структуру двох шляхів. шлях лівої сторони складається з трьох сегментів і двох стрілок, при праві один, це довше складається з чотирьох сегментів і трьох стрілок. Довший є звичайно критичний шлях.

-

Рис 6, Графічне відображення програми Р і її «шляхи», критичний шлях є найдовшим стр(P) = 3.

 

Можливо, що критичний шлях не має ніяких стрілок. У такому разі, критичний шлях складається

тільки з одного процесу. Також можливо, що критичний шлях змінює свій шлях, коли ми просуваємося to P P ′ або від, to P ′ P ″ і в наслідок чого число стрілок може змінватись. Як згадуваолсь раніше ми завжди переймаємо на себе оптимальне локальне планування. Спершу ми показуємо, що для продовження число стрілок в критичному шляху не може зростати.

Нехай стр(P) є числом стрілок в критичному шляху програми Р, і дозволяє стр(P ″) бути числом стрілок в критичному шляху програми Р’ (тобто Р після продовження).

Лема 2:. стр(P) ≥ стр(P ′)

Доказ: Припускають, що стр(P) = m,(m ≥ 0) і що в програмі Р є інший шлях, що складається із кількості стрілок М. Коли ми продовжуємо процеси, шлях з більшими стрілками обов'язково має менше виконання. Потім цей шлях зростає повільніше, ніж критичний шлях. Тому, шлях із більшою кількістью стрілок не може бути критичим.

Отже: стр(P) ≥ стр(P ′).

 

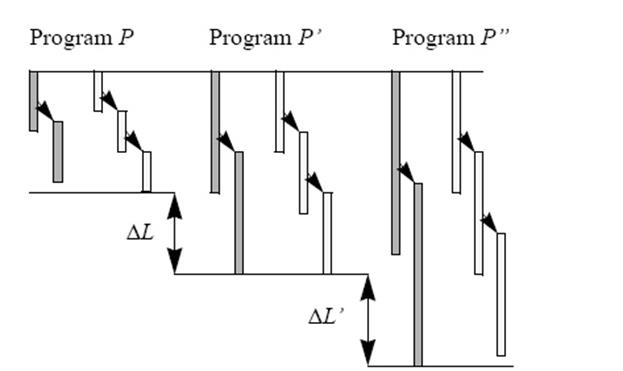
Рис. 7 показує ієрархічну структуру перетворення із статичним розподілом. Програма Р складається з двох шляхів: перший з двома сегментами і одним сигналом синхронізації, і другий шлях з трьома сегментами і двома сигналами синхронізації. Другий шлях довший і це - критичний шлях. Впродовж перетворення перший шлях подовжується швидше і в наслідку це - критичний шлях в програмі P ″.

Розглядаємо, що в програмі Р’ обидва шляхи рівні. В цьому випадку перший шлях з коротшими сигналами синхронізації є

- критичним шляхом. Рис показує також: стр(P)≥стр(P ′) і Δ L ≤ Δ L ′.

Рис 7. Трансформація продовженням

Теорема 1:. Δ L ≤ Δ L ′

Доказ: Нехай E 1 = y 1 + стр(E 1) ⋅ t буде довжиною шляху один, де y1 – сума довжин сегментів (виконання) в шляху один, і стр(E 1) - число стрілок де вартість комунікації = t. Нехай E 2 = y 2 + стр (E 2) ⋅ t буте відповідати довжині шляху два. До того ж, припустимо, що y 1 > y 2 і що шлях два є критичним тобто: E 1 < E 2

 

Нехай E 1′ = y 1(x + Δ x)⁄ x + стр(E 1) t і E 2′ = y 2(x + Δ x)⁄ x + стр(E 2) t шляхи після першого продовження. І нехай тоді E 1″ = y 1(x + 2Δ x)⁄ x + стр(E 1) t і E 2′ = y 2(x + 2Δ x)⁄ x + стр(E 2) t

Будуть шляхами після другого продовження. Потім ми порівнюємо критичний шлях з будь-яким іншим шляхом протягом пролонгацій.

Є три можливі альтернативи:

(1)

Критичний шлях не змінює свою траєкторію, тобто E 1 < E 2 і E 1' < E 2' і E 1'' < E 2''

Тоді: Δ L = E 2′ – E 2

Δ L ′= E 2″ – E 2′= E 2′ – E 2 = Δ L.

 

(2) критичний шлях змінює свій шлях після першого продовження

Тобто E 1 < E 2 E 1' ≥ E 2', і E 1''> E 2'' тоді Δ L < Δ L ′ тому що шлях E 1 росте швидше, ніж E 2.

(3) критичний шлях змінює свій шлях після другого продовження

тобто E 1 < E 2 E 1' ≥ E 2',і E 1''> E 2'' а потім Δ L < Δ L ′, звичайно оскільки шлях E 1 росте швидше, ніж E 2.

Тому, в усіх випадках ми маємо: Δ L ≤ Δ L ′.

 

Ми зараз беремо дві копії програми Р’. З попередньої секції, тому що ми знаємо

що перетворення до м копій програми Р гарантує нам діапазон. Згідно з продовженням перетворення і Теоремою 1, ми маємо:

Теорема 2: 2 L ′ ≤ L + L ″.

Доказ: 2 L ′= L + Δ L + L +Δ L ≤ L +Δ L + L +Δ L ′= L +(L +Δ L +Δ L ′) = L + L ″.

Це означає, що довжина двох копій Р’ (після перетворення Р) є меншою ніж відповідна сума довжин Р і Р’’. Це властивість опуклості перетворення продовження.