
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Найгірша кількість справ, що розглядаються у визначений періодСодержание книги
Поиск на нашем сайте
Нехай L (n, p, J, R) (n > p) означають навантаження на найбільш сильно занавантажееий комп'ютер коли p комп'ютери J = { j 1, …, jp } вимикаються, і використовується схема відновлення R. Нехай L (n, p, R) = max JL (n, p, J, R) для усіх векторів J = { j 1, …, jp }, тобто для усіх комбінації p комп'ютерів, що вимикаються L (n, p, R). визначає поведінку найгіршого випадку після p вимкнень. Ми часто розцінюємо L (n, p, R) як послідовність в змінному p і називають це послідовність навантаження. Наприклад, якщо p = 3 ми маємо: L (n,{1, 2, 3}, R) = <2,2,3>, для (n > p) і схема відновлення R., яка це має на увазі, якщо один комп'ютер ламається, навантаження на найбільш завантажений комп'ютер дорівнює 2, коли два комп'ютери вимикаються, навантаження також дорівнюйте до 2, але коли три комп'ютери вимикаються, потім навантаження на найбільш завантаженому комп'ютер дорівнює 3 (у сценарії найгіршого випадку). Послідовне балансування навантаження Коли є балансування занавантаження, ми надаємо строгий пріоритет маленькому ряду вимкнених комп'ютерів порівнянно з великим числом. Ми називаємо це послідовне балансування навантаження, яке ми потім сформулюємо математично. Ми визначаємо сукупність схем відновлення, це мінімізує максимальне навантаження вимкнених комп'ютерів у формулі:
Відколи L (n, 1, R) = 2 для будь−якого схемного R, ми маємо, мінімізути максимальне навантаження усіх схем, коли тільки один комп'ютер ламається. Потім максимальне навантаження на найбільш завантаженому комп'ютері дорівнює два. Коли два комп'ютери вимикаються, навантаження на найбільш завантажений комп'ютер, можливо, є два або три. Оскільки ми спостерігаємо за мінімумом схеми, це навантаження − два. Зараз, серед схем в R (n, 2) ми вибираємо схеми, які мінімізують навантаження на найбільш завантаженому комп'ютері, коли три комп'ютери вимикаються, щоб сформувати множину R (n, 3). Отже визначенням: R (n, 3) Взагалі ми формуємо R (n, p + 1) вибираючи послідовності відновлення у R (n, p) якому має мінімальним L (n, p + 1, R). Отже R (n, p), не порожній для усього p = 1, …, n – 1 і ми маємо включення R (n, p + 1)с R (n, p) для усього p = 1, …, n – 1.
Відмітьте, що це, там можливо R ∉ R (n, p), існувало б схеми відновлення таким чином, що L (n, p, R)< L (n, p, R ′) R ′ с R (n, p). Потім L (n, i, R)> L (n, i, R ′) для якогось R ′ є R (n, p) і i < p. Це наслідок послідовного балансування навантаження. Послідовність L (n, 1, R), L (n, 2, R),…, L (n, n – 1, R) ідентична для усіх R є R (n, n – 1). Цю оптимальну послідовність навантаження означає SV. Таблиця нижче показує деякі приклади модуля послідовностей 6. Є 5! Можливий послідовності.
Таб. 1 Приклади послідовностей модуля 6.
Ці послідовності прийняті, коли один комп'ютер ламається (належить до R (6,1)). Для двох пошкоджених комп'ютерів послідовності R4 і R5 виключені, залишок належать R (6,2). Для трьох вимкнень R3 виключений, і для чотирьох вимкненьи R2 виключений. У наслідок оптимальна послідовність в цьому прикладі − R1. Якщо ми спостерігаємо тільки за послідовностями R3 і R4 потім ми маємо це не дивлячись на те, що L (6,4, R 4)< L (6,4, R 3), оскільки p = 2, бо ми маємо L (6,2, R 4)> L (6, 2, R 3).
Оптимальні схеми відновлення Послідовності в R (n, p) іноді звані p−оптимальні послідовності. Визначення 1. Множина R *(n) = R (n, n – 1) − сукупність послідовно оптимальних схемвідновлення. Головна мета цієї статті − описати множини для усього n і його навантаження послідовність SV. Порівнянням з попередньою роботою в цьому плані як описано спочатку у Секції 3, такий опис виснажив би це проблемне формулювання. Нехай Не відомо, якщо нижчий MV межі щільні. У цій статті ми розслідуємо напруженість з пов'язаного MV оптимальний послідовність навантаження SV. Ми подали алгоритм, з яким ми обчислюємо оптимальну межу SV. У багатьох зразках, коли ми маємо більший ряд пошкоджених комп'ютерів, SV не співпадають з MV.
Головні результати У цій секції ми подали метод, для досягнення максимального навантаження в найгіршому випадку поведінки після p вимкнень.
Комп'ютерні ланцюги Обчислення оптимальних послідовностей стає здійснимим наступним формулюванням задачі в ланцюгах і об'єднаннях ланцюгів. Щоб вивчати балансування навантаження, ми переключаємо перспективу до точки зору комп'ютера y, який отримує процеси від деякої кількості аварій комп'ютерів. Ланцюг − послідовність xi, 1, xi, 2, …, xi, j списоку відновлення, яка закінчується в комп'ютері y, тобто y = xi, j. Це отже представляє шлях, що i−тий процес (процес i−того комп'ютера) бере, щоб закінчитися в комп'ютері y. Змінна j означає число збійних кроків до y. Якщо, ми говоримо, що цей процес i має відстань j до комп'ютера y. Починаючи з входу для кожного виправленого i в кожному регулярному списку відновлень, існує точно один процес з відстанню j, для усього. Ми, можливо, потім упорядковуємо ланцюги збільшуючи відстань до y: L 1 = { y 1,1} L 2 y 2,1, y 2, 2 = { } Ln – 1 ={ yn –1,1, yn –1,2,…, yn – 1, n – 1} У цій секції усі схеми відновлення і ланцюги перераховуються в змісті модуля. Не може бути двох ланцюгів тієї ж довжини, відколи це мало б на увазі, що процеси були породжені в тому ж комп'ютері. Ми підсумовуємо: кожен ланцюг представляє шлях для процесу, який перенесений з комп'ютера y наступними комп'ютерними вимкненнями. Кожен вхід в ланцюги представляє комп'ютер, який вимкнений. Регулярний список відновлень дає ланцюги: { y – R 1} (mod n) {y – R 2, y – (R 2 – R 1)} (mod n) { y–R3, y –(R 3 – R 1), y-(R3 – R2)} (mod n) … { y – Rn – 1, y –(Rn – 1 – R 1), …, y –(Rn – 1 – Rn – 2)} (mod n)
Ми, можемо, альтернативно описати регулярну схему відновлення R = {0, R 1, …, Rn – 1} різницями r = { r 1, r 2, …, rn – 1}. Ми визначаємо r 1 = R 1 (mod n) r 2 = R 2 – R 1(mod n) r 3 = R 3 – R 2(mod n) … rn – 1 = Rn – 2 – Rn – 1(mod n)
і отже R 1 = r 1(mod n) R 2 = r 1 + r 2(mod n) … Rn – 1 = r 1+ r 2+…+ rn – 1(mod n)
Близькі регулярні схеми відновлення потім дано: 0. { r 1, r 1 + r 2, r 1+ r 2+ r 3, …, r 1+…+ rn – 1} (mod n) 1. { r 1 + 1, r 1 + r 2 + 1, …, r 1+…+ rn – 1+1} (mod n) … n-1 { r 1 + n – 1, …, r 1+…+ rn – 1+ n – 1} (mod n) Ланцюги комп'ютерів, що закінчуються в y, є як зазначено нижче: { y – r 1} (mod n), { y –(r 1 + r 2), y – r 2} (mod n), { y –(r 1+ r 2+ r 3), y –(r 2 + r 3), y – r 3} (mod n), … { y –(r 1+…+ rn – 1), …, y –(rn – 2 + rn – 1), y – rn – 1} (mod n), Властивості, в яких ми зацікавлені, більші легко вивчився в наступній версії: C 1 = { r 1} (mod n), C 2 = { r 1 + r 2, r 2} (mod n), C 3 ={ r 1+ r 2+ r 3, r 2 + r 3, r 3} (mod n), … Cn – 1 ={ r 1+…+ rn – 1, …, rn – 2 + rn – 1, rn – 1} (mod n),
Приклад послідовності Для n = 7 регулярного списку відновлень для комп'ютера 0 є: {, R 2, …, R 6}= {0, 1, 4, 6, 2, 3, 5}, описано відмінності (mod 7) r: { r 1, r 2, …, rn – 1} = {1, 3, 2, 3, 1, 2}. Ланцюги комп'ютерів, що закінчуються в y, є як зазначено нижче: { y – 1} mod 7, { y – 4, y – 3} mod 7, { y – 6, y – 5, y – 2} mod 7, і так далі. Послідовності, що вивчаються є: C 1 = {1} C 2 = {4, 3} C 3 = {6, 5, 2}, і так далі. Отже, ми подали відмінності по діагоналі від низу в трикутнику на Мал. 2.
Мал. 2 Різнецевий трикутник для n = 7
Нормальні послідовності Вимога, щоб входи в R = {0, R 1, …, Rn – 1} − чіткі перетворення для відмінностей r = { r 1, r 2, …, rn – 1} у вимозі, йдеться про те що усі послідовні парні суми не дорівнювали нулю (mod n): Визначення 2. Послідовність r = { r 1, r 2, …, rn – 1} нормальна, якщо Анотація 1: R має чіткі нормальні входи r. Доказ: Ми маємо Rj = Rk 0≤ k ≤ j ≤ n – 1, якщо і тільки якщо Отже, якщо будь-яка послідовна часткова сума − n, то Ri = Rj для деякого i ≠ j. Запису також що модуль один більш ніж довжина послідовності різниці. Наприклад послідовності 1:s тільки нормальні r = {1, 1, 1, …}, відповідають R = {0, 1, 2, …}. Оскільки ми відмітили, там(n – 1)! різний нормальний стан послідовності довжини n – 1. Тільки нормальні послідовності дають корисні схеми відновлення.
|
|||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-22; просмотров: 282; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.139.94.174 (0.011 с.) |


 R (n, 2). Отже, множина R (n, 3) містить схеми відновлення, які мінімізують навантаження, де ми надаємо пріоритет виконанню, коли два комп'ютери − вимкненні понад три комп'ютери вимкнені. Це послідовне балансування навантаження, яке ми потім визначаємо взагалі.
R (n, 2). Отже, множина R (n, 3) містить схеми відновлення, які мінімізують навантаження, де ми надаємо пріоритет виконанню, коли два комп'ютери − вимкненні понад три комп'ютери вимкнені. Це послідовне балансування навантаження, яке ми потім визначаємо взагалі. . Для усіх R
. Для усіх R  R (n), це доводиться в [20] що MV ≤ L (n, j, R) хоча j = 1,2, …, p.
R (n), це доводиться в [20] що MV ≤ L (n, j, R) хоча j = 1,2, …, p.
 для усіх 1 ≤ a ≤ b ≤ n – 1.
для усіх 1 ≤ a ≤ b ≤ n – 1. який вірний, якщо і тільки якщо
який вірний, якщо і тільки якщо 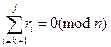 анотація доведена.
анотація доведена.


