
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Властивості розміщення товстої частиниСодержание книги
Поиск на нашем сайте
На час завершення не впливає тотожність процесів розподілив для іншого процесора, тому що, якщо векторний v1 розподіляється на процесорі і векторний v2 розподілений на процесор B, потім переміщаючи v1 до B і v2 еквівалентний до переупорядковування рядів. Очевидно, переупорядковування рядів не впливає на час завершення. Тому час завершення впливають тільки числом векторів розподілив до різних процесорів Q ′. Теорема 4:, Якщо є n1 вектори розподілив на процесорі А і n2 вектори на процесорі B, n 1 < n 2 і, час завершення не може зрости, якщо ми переміщаємо один вектор процесор B до процесора А. Доказ: Ми назначаємо вектори в Q ′ тому, таким чином, що вектори, на яких 1 до n1 n 1 + 1 n 1 + n 2 процесор і вектори розподіляються на процесор B., Ми є зараз збираємось довести, що, переміщаючи векторний номер n 1 + 1 на процесор А, що не збільшить час завершення. Якщо вектор n 1+1 має нуль в слот Якщо час завершення від ряду r зростає від h до h + 1 того, коли ми переміщаємо вектор n 1 + 1 із процесора B до процесор А, має бути h ті в позиції 1 до n1 в ряду r. У такому разі ми знаємо, що симетрія (n1, n2) –переривання гарантоване.
рис 12, Трансформація векторного представлення програми Ку через переривання процесів в тій самій програмі.
Рис 13. (Одне 2-4 переривання і одне 2-3 переривання в тому самому рядку Де щонайменше h + 1 ті в позиціях n 1 + 1 n 1 + n 2 в ряд r'. Позиції n 1+ n 2+1 до n ідентичні в r і r'. Тому час завершення r' зменшиться один, переміщаючи вектор n 1 + 1 з процесора B до процесора А. Тому час завершення Q ′ не може зрости, якщо ми переміщаємо один вектор від процесора B до процесора A. Як наслідок, розміщення Q ′ результатів в коротшому завершенні хронометрують більше порівну процеси, що поширюються на процесорах. Також тотожність процесів не має значення, і ми можемо замовити n векторів в деякому довільному замовленні. Фактично, мінімальний час завершення отримує розподіл векторного номера c + ik процесор c (1 ≤ c ≤ k, 0 ≤ i ≤ n ⁄ k). Обчислення товстої частини Найочевидніший шлях вичислити товсту частину – генерувати (n q) x n матрицю що містить усі можливі перестановки q ті і нулі, і явно обчислити час завершення для цього матричного використовуючого розміщення, що описано в попередній секції. Ми можемо користуватися інформацією що повні програми – погано працюючі, щоб виразитися це обчислення в деякому відношенні яке є по суті більшим чинником (подивіться наступне вирівнювання). Вирівнювання 1. Розглянемо паралельні P програми з n процесами, k комп'ютери в розподіленій системі, q процесори в SMP, і розміщенні А, де aj процеси розподілено для j комп'ютери. Отже, розміщення дає послідовність розміщення (a 1, …, ak), де Тут сума прийнята усі послідовності не заперечення, що зменшуються цілі числа таке, що Тонка частина Результат цієї секції - формула для функції r (A, n, k, t), де А- розміщення з процесів до процесорів. Ця функція - один з двох ключових компонентів ми треба для того, щоб отримати нашу кінцеву мету: H (n, k, q, t, z). в Розділі 4 ми знаємо, що тонка частина програми, для якої коефіцієнт Нехай У рис. 14 оригінальна комунікація вектора для Р3 є, (6-2) означаючи, що це там - шість синхронізація між Р3 і Р2 і двох синхронізацій між Р3 і Р2. В копії, яку ми маємо переставлено частоти комунікації Р2 і Р3 і ми отже маємо шість синхронізацій між Р2і Р3і двох синхронізацій між Р2 і Р3.
Рис 14. Копіювання де ми маємо замінену комунікацію частоти Р2 і Р3
Якщо ми конкатенуємо оригінал (який ми називаємо Р) і копію (яку ми називаємо Q) ми отримуємо нову програму P ′ таку, як Ts (P ′, A, k, t)≤ Ts (P, A, k, t)+ Ts (Q, A, k, t) для будь-якого розміщення А (що використовують відсутність процесу на процесор і відсутність затримок синхронізації). узагальнюючи цей аргумент ми отримаємо вид перестановки, оскільки ми мали для товстої частини (рис. 12). Ці перетворення показують, що найгірше для тонкої частини відбувається, коли усі сигнали синхронізації посилаються від усього часи n процесів - кожного разу до іншого обробника. Усі можливі сигнали синхронізації для n процесів дорівнюють і усім можливим сигналам синхронізації для процесів розподілили для процесору i дорівнює ai (ai – 1)., Тому що деякі процеси виконуються на тому ж процесорі вартість комунікації для них дорівнює нулю. Це означає, що число синхронізації сигналів в програмі (відносно вартості комунікації) рівне
|
||||
|
Последнее изменение этой страницы: 2016-06-22; просмотров: 291; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.189.194.225 (0.01 с.) |

 , вклад в час завершення від ряд r не впливатиме переміщення вектору n 1 + 1 з процесору B процесор А. Тому, нам доведеться тільки розглянути ряди, для яких передача слот один у векторі n 1 + 1. Окрім того, якщо число в позиціях 1 до n1 відноситься як менший, ніж число в позиціях n 1 + 1 n 1 + n 2, вклад в час завершення від ряд r не зросте. Тому, для кожного ряд r таке ця позиція містить один, і там є щонайменше, як багато ті в позиціях 1 до n1, як в позиції, там існує (n 1 ,n 2) переривання r'. (n 1 ,n 2) –переривання отримане перемиканням між i, і n 1+ n 2+1 – i (1≤ i ≤ n 1), (рис 13).
, вклад в час завершення від ряд r не впливатиме переміщення вектору n 1 + 1 з процесору B процесор А. Тому, нам доведеться тільки розглянути ряди, для яких передача слот один у векторі n 1 + 1. Окрім того, якщо число в позиціях 1 до n1 відноситься як менший, ніж число в позиціях n 1 + 1 n 1 + n 2, вклад в час завершення від ряд r не зросте. Тому, для кожного ряд r таке ця позиція містить один, і там є щонайменше, як багато ті в позиціях 1 до n1, як в позиції, там існує (n 1 ,n 2) переривання r'. (n 1 ,n 2) –переривання отримане перемиканням між i, і n 1+ n 2+1 – i (1≤ i ≤ n 1), (рис 13).

 . Тоді:
. Тоді: 
 .
. максимізував складається з послідовності синхронізацій, тобто програма R. Із розділу 5 ми знаємо, що тотожність розподіла процесів для певного процесора не впливає на тривалість виконання товстої частини. Для товстої частини ми маємо оптимальне розміщення, якщо ми уміємо поширювати процеси порівну серед процесорів. У тонкій частині ми захотіли б розподілити процеси, які часто прив'язуються до того ж процесора. Ці цілі є, оскільки ми повинні подивитися, до великої несумісної протяжності.
максимізував складається з послідовності синхронізацій, тобто програма R. Із розділу 5 ми знаємо, що тотожність розподіла процесів для певного процесора не впливає на тривалість виконання товстої частини. Для товстої частини ми маємо оптимальне розміщення, якщо ми уміємо поширювати процеси порівну серед процесорів. У тонкій частині ми захотіли б розподілити процеси, які часто прив'язуються до того ж процесора. Ці цілі є, оскільки ми повинні подивитися, до великої несумісної протяжності. буде послідовністю синхронізації довжини
буде послідовністю синхронізації довжини 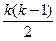 для програми з k процесами. Значення j в цій послідовності вказує число синхронізацій між парою процесів. Оптимальний шлях обов'язкових процесів до процесорів під ці умови максимізував число синхронізацій в межах того ж процесора. Також треба знайти випадки найгіршої синхронізації.
для програми з k процесами. Значення j в цій послідовності вказує число синхронізацій між парою процесів. Оптимальний шлях обов'язкових процесів до процесорів під ці умови максимізував число синхронізацій в межах того ж процесора. Також треба знайти випадки найгіршої синхронізації.
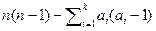 Тому, оптимальний час для тонкої частини з вартістю комунікації t, і розміщенням А є:
Тому, оптимальний час для тонкої частини з вартістю комунікації t, і розміщенням А є: 



