Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Надійність проти ДоступностіСодержание книги
Поиск на нашем сайте
Обчислюючи системи комунікації характеризують фундаментальні властивості: функціональність, виконання, надійність і захист, і вартість (Авізієніс, [3]). Надійність і придатність – дві з п'яти характеристик надійності. Обидві залежать від 2х компонентів: «Середній час між відмовами» (СЧМВ) і Середній час до ремонту (СЧДР). Надійність (R) - здатність обчислювальної системи діяти без невдачі, поки придатність (A) – це готовність для правильного обслуговування. Придатність визначається як пропорція часу, протягом неї система працює (Лапрі [37]):,
Система з 0.999 придатністю надійніша, ніж система з 0.99 придатністю. До того ж, система з 0.99 придатністю має 1 - 0.99 = 0.01 вірогідності відмови. Отже, відмова - F = 1 - і надійність R = 1/(1 - A) (Лапрі [37]). Придатність системи може бути показана як «три 9-ки»), наприклад система з 0.999 придатністю називається «три дев’ятки» і належить, до классу 3. Рис. [4] відбражає класифікацію придатності системи що перведена в середню величину непрацездатності до загального робочого часу (Фістер [54] і Лапрі., [37])
Рис.4 Классифікація доступності систем
Системи класу 4-6 – називаються як системи високої доступності (Фістер, [54]). Підсумок Статей Ця секція підсумовує статті, що залучені в дисертацію. Частина 1 4.1.1 Порівняння оптимального виконання паралельної архітектури (Стаття I) Ця Стаття розширює результати Леннерштадта і Люндберга [39 і 42] де ціністю синхронізації було знехтувано. Тут збільшена межа для користування системою з q процесорами і часом виконання, які обробляють порівнянний перерозподіл до користування системою з k процесорами, деяким перерозподілом і затримкою комунікації t, бо програма представлена з n обробкам и і мірою деталізації синхронізації z. Основне сприяння в цій Статті є те, що ми обробляємо і перевіряємо правильність реалістичнішого комп'ютерної моделі, де затримка комунікації t для кожного сигналу синхронізації і міри деталізації z програми береться до уваги. Ми представили перетворення, які допускають, що ми відділяємо виконання і синхронізацію. Аналізуючи частини окремо і порівнюючи їх, ми знайшли формулу, H (n, k, q, t, z) яка знаходить мінімальний час завершення: H (n, k, q, t, z) = minAH (A, n, k, q, t, z). Тут А означає розміщення процесів до процесорів, де процеси розподіляються для j-ого комп'ютера. Отже, розміщення дає послідовність розміщення, де (a 1, …, ak). До того ж, Частина виконання, представлена вище, відповідає попереднім результатам. Функція g (A, n, k, q) опукла в сенсі що значення зменшується, якщо завантажити найгірші програми випадку,Ж найчастіше поширені серед комп'ютерів. Проте, частина синхронізації, представлена увігнутою r (A, n, k, t) функцією. Ця кількість зростає, якщо завантаження найгіршого випадку програми поширюється більш рівомірно. Це робить мінімізацію суми H біьше делікантною. Тип оптимального розміщення залежить строго від значення tz. Якщо tz маленький, тоді виконання очолює розділи, що представлені навіть на поширення, однорідні оптимальні розділи. Якщо tz великий, то синхронізацію очолює розділ, де усі процеси розподіляються для того ж комп'ютера оптимальні. Ось - приклад обчислення частини виконання програмного вичисленого P спершу формулою а потім користуючись векторним представленням.
Формула тоді A ={ a 1, a 2; a 1 + a 2 = 3}={(1,2), (2, 1)} і I ={ i 1, i 2; i 1 + i 2 = 2}={(1,1),(2, 0),(0, 2)} і тоді
Користуючись векторним представленням програмного P з розміщенням (1,2), ми отримуємо:
4.1.2 Максимальна Вигода Збільшення Числа пріоритетних Переривань в Мультипроцесорному Планування (Стаття 2) Ця стаття узагальнює результати Браума і Шмідта [5]. Ми розкриваємо питання щільної верхньої межі для максимальної вигоди збільшення числа пріоритетних переривань для будь-якої паралелі Програм,що складається з ряду незалежних робіт, користуючись ідентичними процесорами м. Ми обчислюємо,наскільки великим може бути коефіцієнт мінімального робочого інтервалу при використанні i і j пріоритетних перериваннь. Ми порівнюємо i пріоритетних переривань з j пріоритетними перериваннями в найгіршому випадку. Отже, ми дозволяємо j, поки вирішення проблеми [5] відповідає j = m – 1 В цьому випадку, m ≥ i + j +1 який не співпадає j = m – 1 за винятком, i = 0 ми отримуємо оптимальну межу 2(j ⁄(i + 1) + 1)⁄(j ⁄(i + 1) + 2). Наприклад, виключаючи одне пріоритетне переривання (i = j – 1) можем ніколи не псувати робочий інтервал більш ніж на 4/3. Цей аргумент не може виконуватися ітераціями, відколи різна безліч робіт – «найгірший випадок», залежить від параметрів i і j. В цьому випадку ми представили формулу і пост алгоритм, заснований на дереві Stern-Brocot. Частина 2
У толерантних розподілених системах дефекту важко вибрати, на якому процесорі які процеси треба виконувати. Коли усі комп'ютери запущенні, доречним було б завантаження, яке порівну розподіляється. Завантаження на деяких процесорах буде зростати, коли один або більше процесорів відмовляє, але і за цих умов можливо поширювати завантаження як можна рівніше між процесорами, що залишилися працювати. Розподіл завантаження, коли комп'ютер відмовляє, вирішений «списками відновлення процесів СВП» роботи на збійному процессорі. Таким чином, поширення завантаження повністю визначається схемою відовлення для будь-якої безлічі процесорів, які відмовляють. Комп'ютерною наукою проблема переформульована в наступних статтях в іншій математичній проблемй, яка проводить різні схеми статичного відовлення. Відповідні математичні проблеми з відповідними схемами відовлення повертають такі значення:
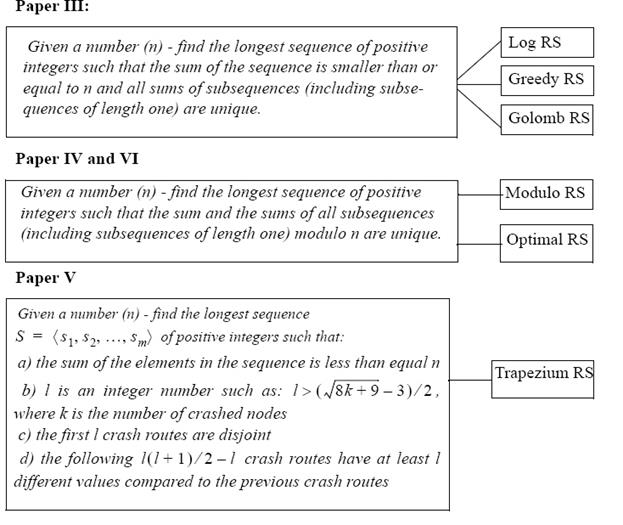
4.2.1 Використання правил Голомбо для Оптимальних Схем Відовлення в системах розподіленої обробки, що мають толерантність до помилок. (Стаття III) Ця стаття розширює результати, представлені в Люддберга і Шавнберга [47]. Тут буде показано як правило Голомбо (послідовність ненегативних цілих чисел таке, що будь-які дві чіткі пари номерів від множини мають ту ж різницю) (Мал. 5) застосовуєтся для проблеми виявлення оптимальної схеми відовлення. Для правила Голомбо відомо довжини аж до 41912 (з 211 мітками) З них перший 373 (з 23 мітками) є оптимальний.
Рис. 5 Списки відновлення Голомбо
Списки відновлення Голомбо відображаються як: Нехай Gn є правилом Голомбо з сумою n + 1 і дозволяє Gn(x) бути x:th входом в Gn наприклад. G12 = <1,4,9,11> і G12 (1) = 1, G12 (2) = 4, і так далі. Нахай потім gn = x кількість збійних комп’ютерів з оптимальною поведінкою, коли ми маємо n комп'ютерів, наприклад g12 = 4. Для проміжних значень k ми користуємося меншим правилом Голомбо і залишковим списком відновлення, наповненим номерами, що залишилися, аж до k -1. Наприклад, заповнене номерами, що залишилися, правило G12 дає список {1,4,9,11,2,3,5,6,7,8,10}. Послідовність посилань на Голомбові схеми відовлення складає в цьому випадку <1,3,5,2> (тобто відмінності між номерами від списку). Цілком інші списки відновлення виходяь від цього додаючи виправлений номер до усіх входів в сенсі модуля, тобто Ri = {(i+ 1) мод n, (i+ 2) мод n, (i+ 3) мод n,., (i+n- 1) мод n }, де Ri – відовлення складіть список для процесу i. Якщо n = 12, який ми отримуємо: R0 = <1,3,5,2>, R1 = <2,4,6,3>, R2= <3,5,7,4> і так далі. У цій статті ми показали також «жадібний» алгоритм, від якого сконструйовано 3 послідовності з чіткими частковими сумами. Це може гарантувати оптимальну поведінку до ⎣log2 n ⎦відмов комп’ютерів, але ми можемо легко вичислити це також для великого n, де немає відомих Голомбових правил. 4.2.2 Використання правил Модуло для Оптимальних Схем Відовлення в Поширюваному Обчисленні (Стаття 4) Стаття IV розширує Голомбову схему відовлення. У формулюванні, яке може бути оброблено правилами Голомбо циклічні переходи проігноровані - тобто це ситуації, коли повне число "переходів" для процесу більше, ніж число комп'ютерів в группі. Ця проблема дає нове математичне формулювання виявлення найдовшої послідовності позитивних цілих чисел - таке, що сума і суми усіх підпослідовностей (у тому числі підпослідовності довжини один) за модулем n унікальні (для цього n). Це математичне формулювання комп'ютерно-наукової проблеми робить новимими потужнішими схемами відовлення так звані схеми Модуло, які є оптимальними для більшості з ряду пошкоджених комп'ютерів. Списки (відовлення схема) конструюються так само, як Голомбові або «Жадібні» списки відновлення (схема). Рис 6
Мал. 6 Послідовність Модуло для н=11 із усіма вдмінностями
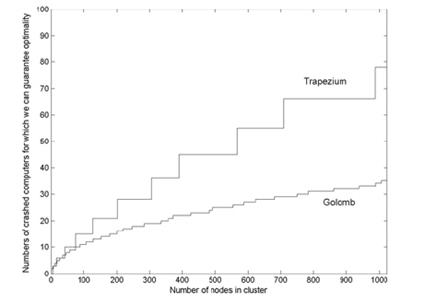
4.2.3 Розширені Правила Голомбо як Нові Схеми Відовлення в Залежно-розподіленому обрахунку (Стаття 5) В цю статтю ми включаємо нові схеми відовлення, що називаються схемами відовлення трапеції, де перша частина схем заснована на відомому Правилі Голомбо, (тобто збійні маршрути не перетинаються), а в другій частині сконструйовано шлях, де наступні збійні маршрути, які мають в найменше значення l, унікальні у порівнянні з попереднім збійним маршрутом. Схеми відовлення трапеції гарантують краще виконання, ніж схеми Голомбо і прості для обчислення. Мал. 7 порівнянь число відмов схеми трапеції, з виконанням схеми використовуючи правила Голомбо як функцію числа вузлів в групі (n) аж до n = 1024.
Рис.7 Різниця між трапеціальною і голомбовою схемами
Мета цієї статті знайти хороші схеми відовлення, це краще, ніж вже відомо і мають легко вичислити також для великого n. У Статті 5 ми знайшли кращі можливі схеми відовлення для будь-якого числа пошкоджених вузлів в групі. Знайдіть, що така схема відовлення - дуже складне для обчислення завдання. Із-за складності проблеми ми тільки змогли представити схеми відовлення максимум для 21 вузла в групі. 4.2.4 Оптимальні Схеми Відовлення в Розподілене обчислення з толерантністью до помилок (Стаття 6)
У Статті 6 ми обчислюємо кращі можливі схеми відовлення для будь-якого числа пошкоджних комп’ютерів при наданні строгого пріоритету маленькому ряду непрацюючих машин порівняно з великою їх кількістью. Засоби, що ми вибираємо - це безліч схем відовлення найгірших ситуацій у порівнянні з оптимальною поведінкою, коли два комп'ютери відмовляють, і серед них виберають схеми відовлення, які мають оптимальну поведінку, коли три комп'ютери відмовляють і так далі. Ми визначаємо безліч схем відовлення, це мінімізує максимальне навантаження за 1,2,..., p формулу «помираючих комп’ютерів»
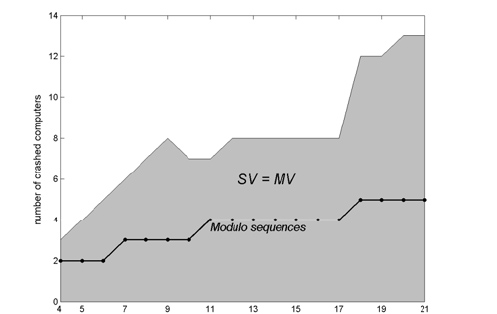
Рис 8. Порівняння оптимальних послідовностей схем відновлення до послідовностей Модуло
Нижня щільна межа MV є невідомою. У цій статті ми розслідуємо напруженість пов'язану з MV оптимальною послідовністю завантаження SV. Ми покажемо алгоритм за яким ми обчислюємо оптимальну межу SV. У багатьох зразках, коли ми маємо більший ряд пошкоджених комп'ютерів, SV не співпадають з MV. Мал. 8 показів якою MV є щільною мірою. У сірій області MV є щільний, починаючи з MV = SV. Для більших величин пошкодженого комп'ютери q, MV < SV, так MV не є щільним . Робота в майбутньому. Межі, що ми отримали в Статті 1, щільні в межах проблеми формулювання. Проте, є область можливостей знайти нові формулювання як у більш специфічних, так і загальніших практичних ситуаціях, де ще не має ніякої відповіді, але де справжній результати, можливо, забезпечує корисну основу для знаходження відповідей. Статті 1 і 2 - фактично розширення заздалегідь вивченогї (оптимально вирішеної) проблеми. Не кажучи вже безпосередньо про результати, це головний вклад в дослідницьку галузь, і він виконаний у цій роботі. З математичної точки зору, результати відкрили нові підключення між паралельними комп'ютерним виконанням і комбінаторикою. Правила Голомбо знайшли нові застосування, і нові комбінаторні проблеми було вирішено. Ці проблеми, можна, вивчати і вдосконалювати як математичні, які потім можуть бути інтерпретовано в комп'ютерному налаштуванні. Нове застосування дерева Stern-Brocot це лише один із прикладів. Я вважаю, що можливо знайти більше таких співпадінь між комп'ютерними розробками і комбінаторикою. 6 Список літератури 1. Ahmad, I., Kwok, Y.-K., and Wu, M.-Y., Analysis, Evaluation, and Comparison of Algorithms for Scheduling Task Graphs on Parallel Processors, in Proceedings of the International Symposium on Parallel Architectures, Algorithms, and Networks, Beijing, China, June 1996, pp. 207-213 2. Avizienis, A., Design of Fault-Tolerant Computers, in Proceedings of Fall Joint Computer Conference, AFIPS Conference Proceeding, Vol. 31, Thompson Books, Washington, D.C., 1967, pp. 733-743 3. Avizienis, A., Laprie, J.-C., Randell, B., and Landwehr, C., Basic Concepts and Taxonomy of Dependable and Secure Computing, IEEE Transactions on Dependable and Secure Computing, Vol. 1, No. 1, January-March 2004, pp. 11-33 4. Blazewicz, J., Ecker, K. H., Pesch, E., Schmidt, G., Weglarz, J., Scheduling Computer and Manufacturing Processes, Springer Verlag, New York, NY 1996, ISBN 3-540-61496-6 5. Braun, O., Schmidt, G., Parallel Processor Scheduling with Limited Number of Preemptions, Siam Journal of Computing, Vol. 32, No. 3, 2003, pp. 671-680 6. Bruno, J., Coffman Jr., E.G., and Sethi, R., Scheduling Independent Tasks To Reduce Mean Finishing Time, Communications of the ACM, Vol. 17, No. 7, July 1974, pp. 382-387 7. Burns, A., and Wellings, A., Real-Time Systems and Programming Languages, Third Eddition, Pearson, Addison Wesley, ISBN: 0-201-72988-1 8. Casavant, T. L., Kuhl, J. G., A taxonomy of Scheduling in General-Purpose Distributed Computing Systems, IEEE Transactions on Software Engineering, Vol. 14, No. 2, February 1988, pp. 141-154 9. Chabridon, S., Gelenbe, E., Failure Detection Algorithms for a Reliable Execution of Parallel Programs, in Proceedings of the 14th Symposium on Reliable Distributed Systems, SRDS'14, Bad Neuenahr, Germany, September 1995 10. Coffman Jr., E. G., Computer and Job-Scheduling Theory, John Wiley and Sons, Inc., New York, NY, 1976 11. Coffman Jr., E. G., Garey, M. R., Proof of the 4/3 Conjecture for Preemptive vs. Nonpreemptive Two-Processor Scheduling, Journal of the ACM, Vol. 40, No. 5, November 1993, pp. 991-1018, ISSN:0004-5411 12. Coffman Jr., E. G., Garey, M. R., Johnson, D. S., An Application of Bin Packing to Multiprocessor Scheduling, SIAM J. Computing, 7 (1978), pp. 1-17 13. Coffman Jr., E. G., Graham, R., Optimal Scheduling for Two-Processor Systems, Acta Informatica, 1 (1972), pp. 200-213 14. Cristian, F., Understanding Fault Tolerant Distributed Systems, Journal of the ACM, Vol. 34, Issue 2, 1991 15. Dollas, A., Rankin, W. T. and McCracken, D., A New Algorithm for Golomb Ruler Derivation and Proof of the 19 Marker Ruler, IEEE Trans. Inform. Theory, Vol. 44, No. 1, January 1998, pp. 379-382 16. El-Rewini, H., Ali, H. H., and Lewis, T. G., Task Scheduling in Multiprocessor Systems, IEEE Computer Vol. 28, No. 12, December 1995, pp. 27-37 17. El-Rewini, H., Ali, H. H., Static Scheduling of Conditional Branches in Parallel Programs, Journal of Parallel and Distributed Computing, Vol. 24, No. 1, January 1995, pp. 41-54 18. Flynn, M.J., Very High-Speed Computing Systems, Proceedings of the IEEE, Vol. 54, No. 12, 1966, pp. 1901-1909 19. Friesen, D. K., Tighter Bounds for the Multifit Processor Scheduling Algorithm, SIAM Journal of Computing, 13 (1984), pp. 170-181 20. Friesen, D. K., and Langston, M. A., Evaluation of a MULTIFIT-Based Scheduling Algorithm, Journal of Algorithms, Vol. 7, Issue 1, March 1986, pp. 35-59 21. Garey, M. R. and Johnson, D. S., Computers and Intractability - A Guide to the Theory of NP-Completeness, W. H. Freeman and Company, New York, 1979 22. Gelenbe, E., A Model for Roll-back Recovery With Multiple Checkpoints, in Proceedings of the 2nd ACM Conference on Software Engineering, October 1976, pp. 251-255 23. Gelenbe, E., Chabridon, S., Dependable Execution of Distributed Programs, Elsevier, Simulation Practice and Theory, Vol. 3, No. 1, 1995, pp. 1-16 24. Gelenbe, E., Derochete, D., Продуктивність of Rollback Recovery Systems under Intermittent Failures, Communication of the ACM, Vol. 21, No. 6, June 1978, pp. 493-499 25. Gerasoulis, A., Yang, T., A Comparisons of Clustering Heuristics for Scheduling DAG’s on Multiprocessors, Journal of Parallel and Distributed Computing, 16, 1992, pp. 276-291 26. Graham, R. L., Bounds for Certain Multiprocessing Anomalies, Bell System Technical Journal, Vol. 45, No. 9, November 1966, pp.1563-1581 27. Graham, R. L., Bounds on Multiprocessing Timing Anomalies, SIAM Journal of Applied Mathematics, Vol. 17, No. 2, 1969, pp. 416-429 28. Graham, R. L., Lawler, E. L., Lenstra, J. K., Rinnooy Kan, A. H. G., Optimization and Approximation in Deterministic Sequencing and Scheduling: A Survey, Annals of Discrete Mathematics 5, 1979, pp. 287-326 29. Hochbaum, D. S., Shmoys, D. B., Using Dual Approximation Algorithms for Scheduling Problems Theoretical and Practical Results, Journal of the ACM (JACM), Vol. 34, Issue 1, January 1987, pp. 144-162 30. Hou, E. S. H., Hong, R., and Ansari, N., Efficient Multiprocessor Scheduling Based on Genetic Algorithms, Proceedings of the 16th Annual Conference of the IEEE Industrial Electronics Society - IECON'90, Vol II, Pacific Grove, CA, USA, IEEE, New York, November 1990, pp. 1239-1243 31. Hu, T. C., Parallel Sequencing and Assembly Line Problems, Operations Research, Vol. 19, No. 6, November 1961, pp. 841-848 32. Kameda, H., Fathy, E.-Z. S., Ryu, I., Li, J., A продуктивність Comparison of Dynamic vs. Static Load Balancing Policies in a Mainframe - Personal Computer Network Model, Information: an International Journal, Vol. 5, No. 4, December 2002, pp. 431-446 33. Karp, R. M., Reducibility Among Combinatorial Problems, in R. E. Miller and J. W. Thatcher (editors): Complexity of Computer Computations. New York, 1972, pp. 85–104 34. Khan, A., McCreary, C. L., and Jones, M. S., A Comparisons of Multiprocessor Scheduling Heuristics, in Proceedings of the 1994 International Conference on Parallel Processing, CRC Press, Inc., Boca Raton, FL, pp. 243-250 35. Krishna, C. M., Shin, K. G., Real-Time Systems, McGraw-Hill International Editions, Computer Science Series, 1997, ISBN 0-07-114243-6 36. Kwok, Y-K., and Ahmad, I., Static Scheduling Algorithms for Allocating Directed Task Graphs to Multiprocessors, ACM Computing Surveys, Vol. 31, No. 4, December 1999, pp. 406-471 37. Laprie, J.-C., Avizienis, A., Kopetz, H., Dependability: Basic Concepts and Terminology, 1992, ISBN:0387822968 38. Lawler, E. G., Lenstra, J. K., Rinnooy Kan A. H. G., Shmoys, D. B., Sequencing and Scheduling: Algorithms and Complexity, S.C. Graves et al., Eds., Handbooks in Operations Research and Management Science, Vol. 4, Chapter 9, Elsevier, Amsterdam, 1993, Chapter 9, pp. 445-522 39. Lennerstad, H., Lundberg, L., An Optimal Execution Time Estimate of Static versus Dynamic Allocation in Multiprocessor Systems, SIAM Journal of Computing, 24 (4), 1995, pp. 751-764 40. Lennerstad, H., Lundberg, L., Generalizations of the Floor and Ceiling Functions Using the Stern-Brocot Tree, Research Report No. 2006:02, Blekinge Institute of Technology, Karlskrona 2006 41. Lennerstad, H., Lundberg, L., Optimal Combinatorial Functions Comparing Multiprocessor Allocation Продуктивність in Multiprocessor Systems, SIAM Journal of Computing, 29 (6), 2000, pp. 1816-1838 42. Lennerstad, L., Lundberg, L., Optimal Scheduling Combinatorics, Electronic Notes in Discrete Mathematics, Vol. 14, Elsevier, May 2003 43. Liu, C. L., Optimal Scheduling on Multiprocessor Computing Systems, in Proceedings of the 13th Annual Symposium on Switching and Automata Theory, IEEE Computer Society, Los Alamitos, CA, 1972, pp. 155-160 44. Lennerstad, H. and Lundberg, L., An Optimal Execution Time Estimate of Static versus Dynamic Allocation in Multiprocessor Systems, SIAM Journal of Computing, 24 (4), 1995, pp. 751-764 45. Lundberg, L., Продуктивність Bounds on Multiprocessor Scheduling Strategies for Chain Structured Programs, Computer Science Section of BIT, Vol. 33, No. 2, 1993, pp. 190-213 46. Lundberg, L., Lennerstad, H., Klonowska, K., Gustafsson, G., Using Optimal Golomb Rulers for Minimizing Collisions in Closed Hashing, Proceedings of Advances in Computer Science - ASIAN 2004, Thailand, December 2004; Lecture Notes in Computer Science, 3321 Springer 2004, pp. 157-168 47. Lundberg, L., and Svahnberg, C., Optimal Recovery Schemes for High-Availability Cluster and Distributed Computing, Journal of Parallel and Distributed Computing 61(11), 2001, pp. 1680-1691 48. Markatos, E. P., and LeBlanc, T. B., Locality-Based Scheduling for Shared Memory Multiprocessors, Technical Report TR93-0094, ICS-FORTH, Heraklio, Crete, Greece, August 1993, pp. 2-3 49. McCreary, C., Khan, A. A., Thompson, J. J., and McArdle, M. E., A Comparison of Heuristics for Scheduling DAG’s on Multiprocessors, in Proceedings of the Eighth International Parallel Processing Symposium, April 1994, pp. 446-451 50. McNaughton, R., Scheduling with Deadlines and Loss Functions, Management Science, 6, 1959, pp. 1-12 51. Nanda, A. K., DeGroot, D. and Stenger, D. L., Scheduling Directed Task Graphs on Multiprocessors Using Simulated Annealing, Proceedings of the IEEE 12th International Conference on Distributed Computing Systems, Yokohama, Japan, IEEE Computer Society, Los Alamitos, June 1992, pp. 20-27 52. Pande, S. S., Agrawal, D. P., and Mauney, J., A Threshold Scheduling Strategy for Sisal on Distributed Memory Machines, Journal on Parallel and Distributed Computing, Vol. 21, No. 2, May 1994, pp. 223-236 53. Papadimitriou, C. H., and Yannakakis, M., Scheduling Interval-Ordered Tasks, SIAM Journal on Computing, Vol. 8, 1979, pp. 405-409 54. Pfister, G. F., In Search of Clusters, The Ongoing Battle in Lowly Parallel Computing, Prentice Hall PTR, 1998, ISBN 0-13-899709-8 55. Pinedo, M., Scheduling: Theory, Algorithms, and Systems (2nd Edition), Prentice Hall; 2 edition, 2001, ISBN 0-13-028138-7 56. Shirazi, B., Kavi, K., Hurson, A. R., and Biswas, P., PARSA: A Parallel Program Scheduling and Assessment Environment, in Proceedings of International Conference on Parallel Processing, ICPP 1993, August 1993, Vol. 2, pp. 68-72 57. Shirazi, B., Wang, M., Analysis and Evaluation of Heuristic Methods for Static Task Scheduling, Journal of Parallel and Distributed Computing Vol. 10, No. 1990, pp. 222-232 58. Soliday, S. W., Homaifar, A., Lebby, G. L., Genetic Algorithm Approach to the Search for Golomb Rulers, in Proceedings of the International Conference on Genetic Algorithms, Pittsburg, PA, USA, 1995, pp. 528-535 59. Tang, P., Yew P.-C., and Zhu, C.-Q., Impact of Self-Scheduling Order on Продуктивність of Multiprocessor Systems, in Proceedings of the 2nd international conference on Supercomputing, June 1988, St. Malo, France, pp. 593-603 60. Ullman, J. D., NP-Complete Scheduling Problems, Journal of Computer and System Sciences, Vol. 10, 1975, pp. 384–393 61. Vaidya, N. H., Another Two-Level Failure Recovery Scheme: Продуктивність Impact of Checkpoint Placement and Checkpoint Latency, Technical Report 94-068, Department of Computer Science, Texas A&M University, December 1994 62. Yue, M., On the Exact Upper Bound for the Multifit Processor Scheduling Algorithm, Annals of Operations Research, Vol. 24, No. 1, December 1990, pp. 233-259 63. Zapata, O. U. P., Alvarez, P. M., EDF and RM Multiprocessor Scheduling Algorithms: Survey and Performance Evaluation, Report No. CINVESTAV-CS-RTG- 02. CINVESTAV-IPN, Computer Science Department, CINVESTAV-IPN, Mexico
СТАТТЯ 1 Стаття 1 «Порівняння оптимальних Архітектур в паралельному обчисленні» Анотація Розглянемо, паралельу програму з n обробками і вагою деталізації синхронізації z. Розглянемо також дві паралельних архітектури: SMP з q процесорами і перерозподілом під час виконанняз процесів до процесорів, і розподіленої системи (чи групи) з k процесорами що не мають перерозподілу під час виконання. Є затримка комунікації міжпроцессорнної одиниці t часу для системи без перерозподілу під час виконання. У цій Статті ми визначаємо функцію H (n, k, q, t, z) часу мінімального завершення для усіх програм з n обробками і мірою деталізації z - у більшості часи H (n, k, q, t, z) довші при порівнянні користування системою без перерозподілу і k процесорами з користуванням системою з q процесорами і перерозподілом під час виконання. Ми переймаємо на себе оптимальне розміщення і планування процесів до процесорів. Функція H (n, k, q, t, z) оптимальна якщо є щонайменше одна програм, з n обробками і мірою деталізації z, така, що коефіцієнт є точно H (n, k, q, t, z). Ми також перевіряємо правильність їх результатів, користуючись вимірами що поширюються і на багатопроцесорні середовища Сан/Solaris. Функція забезпечує важливі інтуїтивні підходи відносно подуктивності значень фундаментального дизайну рішення того, чи дозволити перерозподіл під час виконання процесів чи ні. Ці інтуїції можуть бути використан проектуючи платформи паралельної обробки, роблячи належні ціна/вигода або інші компроміси. Вступ Є багато шляхів введення в дію мультипроцессорних комп’ютерних систем, наприклад слабо пов’язаних розподілених систем що складаються із поодиноких комп’ютерів [1,2], систем з розподіленою спільною пам’яттю [3,4,5], чи жорстко пов'язаних SMP. У деяких випадках, мультипроцесори спільно використовують багато незалежних програм. Проте людина часто зацікавлена в поліпшенні виконання (скорочення часу завершення виконання) однієї паралельної програми, що складається з ряду синхронізуючих процесів (або потоків). Проектуючи багатопроцесорні системи, які підтримують ефективне виконання однієї паралельної програми, дехто стикається з фундаментальним рішенням перерозподілу під час виконання процесу від одного процесора до іншого, або якщо процес повинен виконуватися на тому ж процесорі впродовж повного виконання. Системи, які не роблять дозвіл перерозподілу під час виконання - загалом менші і дешевші для створення. Місткість, і отже вартість, з системи зв'язку є також загалом вище у системах, які підтримують перерозподіл процесу часу виконання. Дозвіл перерозподілу процесу часу виконання у мультипроцесорах з дуже великим рядом процесорів був би дуже важким і дорогим. Очевидний недолік заборони перерозподілу під час виконання є те, що завантаження, можливо, стає неврівноваженим, відколи деякі процесори, можливо, дуже зайняті, поки інші неактивні. Тому немає єдиної відповіді на питання, чи перерозподіл під час виконання треба дозволяти чи ні; Це - технічне рішення, де багато чинників слід взяти до уваги. Дозволяючи перерозподіл під час виконання або розподіл, що безпосередньо не підключений до жорстко пов'язаного SMP або розподіленої системи, починаючи з перерозподілу під час виконання, можливий (але більш дорогий) на розподіленій системі і в деяких SMP, які ми хочемо обмежити, або навіть виключити для того, щоб поліпшити натиснутий коефіцієнт кешів процесора. Один дуже важливий чинник - заборонити чи дозволити перерозподіл під час виконання, який не принесе вигоди для продуктивності, отже зробити завантаження більше збаланснованим. Очевидно, що продуктивність системи, що не використовує перерозподіл навантаження і користується більш слабкими графіками і плануваннями буде менша. Виявлення оптимального мультипроцесора планування і алгоритмів розміщення розподілу ресурсів – ще проблема НП-комплексності [6]. Є, проте, ряд хороших евристичних методів [7,8], і, отже, можливо прийти близько або навіть дуже близько до оптимального результату для багатьох важливих випадків. Одне важливе питання, скільки виконань один отримає дозволяючи перерозподіл під час виконання за умови, що ми можемо знайти (майже) оптимальне планування і алгоритми розміщення. Є очевидно, що ця вигода залежатиме від паралелі програм, в яких ми зацікавлені. Наприклад, якщо ми маємо мультипроцесор з k процесорами, не буде ніякої вигоди для продуктивності дозволу програми перерозподілу під час виконання з 4k паралеллю обробляючими, де усі роблять ту ж кількість роботи (яку ми розмістимо чотирьох процесів на кожному процесорі і закінчуються з абсолютно балансним завантаженням). Для деяких інших програм, там буде вигода у продуктивності при дозволі перерозподілу під час виконання, навіть якщо ми користуємося кращим можливим плануванням і алгоритмами розміщення. Релевантне питання отже було б «скільки один може отримати користь у більшості дозволяючи перерозподілу під час виконання, за умови, що ми користуємося (майже) оптимальним плануванням і розміщенням». Відповідь на це фундаментальне питання забезпечила б важливе рышення, коли ми хочемо збалансувати додаткову вартість і складність дозволу перерозподілу під час виконання проти вигоди продуктивності при дозволі перерозподіл під час виконання. У цій Статті ми визначаємо функцію, яка відповідає на це питання для дуже широкого діапазону мультипроцесорів і паралельних програм. Стаття організована наступним чином. Секція 2 мала показувати відношення попередніх результатів. Секція 3 описує визначення динамічного і статичного розподілу і відмінностей між ними. У Секціях 4 - 7 ми робимо перетворення програми, і показуємо, що перетворення дають у найгіршому випадку. Тобто, програма для якої продуктивність вигода користування SMP, у порівнянні з розподіленими системами, максимальна. Оптимальне розміщення процесів в погано працюючих программах і головний результат статті представляються в Секції 7. Секція 8 перевіряє правильність результатів, використовуючи поширення і багатопроцесорне технічне забезпечення, і Секція 9 обговорює деякі практичні застосування з результату. Нарешті, в Секції 10 додано наші заключення. Попередні результати Це повідомлення розширює результати в [9] і [10]. У цих і попередніх докладах ціною синхронізації було знехтувано. Самі розподілені системи (і інші системи, які не дозволяють перерозподілу) процесу часу виконання, мають істотну вартість за міжпроцессорну синхронізацію. Нехтуючи цією вартістю в системі, яка не дозволить перерозподілу під час виконання процесів, ми отримали занадто короткий час завершення в цій архітектурі. Це означає, що межа на максимальній вигоді користування SMP з перерозподілом під час виконання, у порівнянні з розподіленою системою без часу виконання перерозподілу, можливо, стає занадто низьким, тобто межа в [9] і [10] є фактично не ефективною для найбільше розподілених систем. Помилка, викликана при нехтуванні синхронізацією вартості залежить від частоти (міра деталізації) синхронізації паралельної програми, тобто для того, щоб не нехтувати вартістю синхронізації, треба взяти до уваги міру деталізації програм. Формули в Секції 7 визначають кількість помилок зневаги вартості синхронізації як функції реальної синхронізації вартість в розподіленій системі і мірі деталізації програми. Малюнок 17 (цій статті) показує це графічно; ґрунтуючись на результатах в [9] і [10] ми були тільки здатні проводити верхню графу в Малюнку 17. Розгляд вартості синхронізації і програмної міри деталізації значно ускладнює математична проблема. Оптимальні програми можна все ще характеризувати, але у цьому сценарії ми не можемо характеризувати оптимальні розміщення (який був можливий в [9] і [10]). Докази в Секції 5 змогли використовуватися багаторазово від попередньої роботи, тоді як докази в секціях 4, 6 і 7 нові і оригінальні. У [9] оптимальна верхня межа на вигоді користування розподілених системам SMP торкається випадку, де число комп'ютерів в розподіленій системі дорівнює числу процесорів в SMP. Сценарій також представляє статико/ динамічний розподіл на тому ж мультипроцесорі. У [10] це озписано для групи розміщення різного числа процесорів.
|
||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-22; просмотров: 455; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.227.0.21 (0.031 с.) |

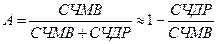 якщо СЧМВ значно більший, ніж СЧДР.
якщо СЧМВ значно більший, ніж СЧДР. прийнята усі послідовності I = { i 1, …, ik } що зменшується з ненегативних цілих чисел, таке,
прийнята усі послідовності I = { i 1, …, ik } що зменшується з ненегативних цілих чисел, таке, 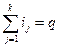 що. H (A, n, k, q, t, z) = g (A, n, k, q)+ zr (A, n, k, t), де
що. H (A, n, k, q, t, z) = g (A, n, k, q)+ zr (A, n, k, t), де 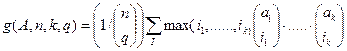 .
.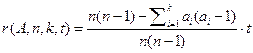


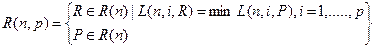 де L(n, p, R) є послідовністю завантаження і визначає поведінку окремо взятого випадку після того, як p руйнується, коли використовується схема відовлення R., оптимальну послідовність завантаження означає SV.
де L(n, p, R) є послідовністю завантаження і визначає поведінку окремо взятого випадку після того, як p руйнується, коли використовується схема відовлення R., оптимальну послідовність завантаження означає SV. 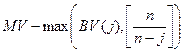 , де BV вектор границі (межі) що містить саме К записів, що рівні К де k ≥ 2
, де BV вектор границі (межі) що містить саме К записів, що рівні К де k ≥ 2