Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Формування проблем, позначення і основні результати.Содержание книги
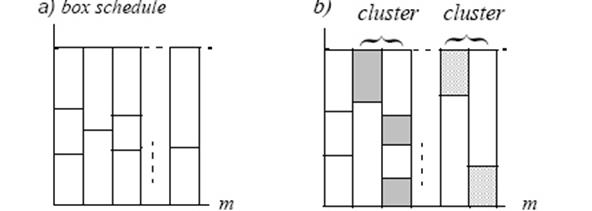
Поиск на нашем сайте Формулювання завдання Ми розглядаємо мультипроцесор з ідентичними процесорами м і паралельною програмою P, що складається з n процесів незалежних процесів. Звичайно, P, можливо, також назвати безліччю робіт. Тільки дійсна змінна роботи - її тривалість (так звана довжина) виконання. Метою є мінімізація робочого інтервалу P, тобто робочий інтервал з оптимальним графіком. Мінімальний робочий інтервал P на м процесорах, при користуванні i пріоритетними перериваннями означають C (P, m, i). Ми розглядаємо два плануючих випадки: коли програма оптимально планується на мультипроцесорі користуючись у більшості i пріоритетними перериваннями, і так само з j пріоритетними перериваннями, де ми переймаємо на себе i < j. Немає ніяких накладних витрат для планування процесу, перемикання контексту або перерозподілу. Відколи ми розглядаємо планування з i і j пріоритетними перериваннями, ми використовуватимемо зображення знаками в якості i-планування і j- планування, i- робочий інтервал і j- робочий інтервал, і так далі. Для програмного P ми зацікавлені в тому, як крупно коефіцієнт C (P, m, i)⁄ C (P, m, j) може бути. Означимо G (m, i, j) = max PC (P, m, i)⁄ C (P, m, j), де максимум узятий над усіма програмами P. Очевидно, коефіцієнт C (P, m, i)⁄ C (P, m, j) зменшується як функція i і зростаючи як функція j, якщо інші змінні постійні. Ці властивості тримають також для G (m, i, j). Позначення і терміни Програмний P', для якого C (P ′, m, i)⁄ C (P ′, m, j) = max PC (P, m, i)⁄ C (P, m, j) де максимум прийнятий усе програми P, званий екстремальною програмою де усі процесори стартують і зупиняються одночасно (Мал. 1a). До того ж, ми говоримо, що процесори, які спільно використовують роботу, до і після пріоритетного переривання, пов'язані. Це дає розділ процесорів в множинах, де пари процесорів знаходяться в тій же множині, якщо вони пов'язані, безпосередньо або побічно через інші процесори, які, можливо, формують ланцюжки пов'язаних процесорів. Безліч процесорів, де усі процесори пов'язані один з одним таким чином званий групою пріоритетних переривань (Мал. 1b)., Якщо це може плануватися як графік блоку, це має час завершення kx/c, де x - середнє значення разів завершення для робіт, k - число робіт, і c є число процесорів. Графік блоку можливий за винятком часу завершення один єдиний процес більший, ніж kx/c [14]. Групи пріоритетного переривання завжди розглядаються щоб плануватися з графіком блоку, якщо можливо, починаючи з цього очевидно дає мінімальний час завершення для групи. Критичний процесор - останній процесор для завершення - це завершується в робочому інтервалі програми. Безліч робіт на критичному процесорі може також зватись критичний, також як і кластерне закінчення в глобальному робочому інтервалі.
Рис 1 Приклад коробочного планування «а» і коробочне планування із переривчастими кластерами «б» (білі прямокутники показують неперервні роботи) Ми позначаємо число робіт програми n. McNaughton кручене правило [14] забезпечує оптимальний графік для машин м паралелі, використовуючи в найбільше м- 1 пріоритетне переривання. Це правило просто конкретизує, що k - атий перервав 1 ≤ k ≤ m – 1 роботу, запуски у k:тому процесорі і закінчує в (k + 1) процесорі. Така група звана Група McNaughton-а. Для групи McNaughton з i ≥ 1 пріоритетними перериваннями процесори включені, як мінімум i + 2 роботи. Чиста група McNaughton має точно i + 2 роботи. Невивантажена робота, яка планується на процесорі, який не має ніяких інших робіт, буде будьте названа єдиною роботою. Вежа посилається на графіки планування в процесорі, де усі роботи невивантажені. Вежа складається з k робіт позначається як k-tower. Основний результат Основні результати - наступне: Теорема 1: Для усіх цілих чисел м >0 і 0 ≤ i < j, ми маємо:
Кількість Докази Методи доведення Обчислити формулу G (m, i, j) = max PC (P, m, i)⁄ C (P, m, j) характеристики підмножини екстремальних програм із структурним досить, щоб бути здатним сформулювати формулу. Це призводить до чисто математичного формулювання, яке розглянуто і вирішено в [12]. Ми починаємо з показу, що є екстремальні програми, які мають блочне j-планування. Лема 1: (Продовження) Розглядають програмний P з оптимальним j-планування. Ми еретворюємо P в програмі P., подовжуючи деякі з робіт таким чином, що усі процесори є постійно зайнятий C (P, m, j) таким чином, що C (P, m, j) = C (P ′, m, j). Доказ: Ця зміна не може зменшити i- робочий інтервал, але, можливо, збільшує при незмінному j- робочому інтервалі. Цією лемою нам тільки треба розглядати програми, які мають оптимальне i-планування яке є графіком блоку. Якби тільки явно заявлено інакше, ми нормалізуємо j -робочий інтервалдо 1. Від цієї нормалізації це звичайно слідує, що сума усього виконання часу програми на м процесорах - м. Ми надалі розглядаємо тільки такі програми. 3.2. Перевищення програми P' Лема 2: У найгіршому випадку програма P', яка має m + i +1 роботи, де усі роботи у тій же j-cluster мають той же розмір, і де дві найменші роботи не вивантажено. Отже, критичний процесор обробляє 2-опори. Доказ: Як частину нашого доказу ми тимчасово представляємо обмеження планування роботи по дорозі до процесорів, користуючись i пріоритетними перериваннями. Це обмеження визначається оптимальним графіком тих же програмних використовуючих j пріоритетних переривань. Без втрати загальності ми, можливо, припускаємо, що оптимальний графік, що користується j пріоритетними перериваннями, складається з c пріоритетного переривання групи. Кожна така група складається з одного або більше процесорів - група визначає специфіку групи процесорів, які релевантні також для i-планування. Це має на увазі це там - група процесорів, що асоціюються з кожною групою пріоритетних переривань. Тимчасове обмеження на i-планування, який ми представляємо, як усі роботи, на яких планується процесор в груповому k 1 ≤ k ≤ c в цьому оптимальному j-плануванні належать до тієї ж групи процесорів в i-плануванні. Через майбутній порякок обговорення і базуючись на попередньому обговоренні виникає [2] ми отримаємо екстремальну програму і екстремальний коефіцієнт під цим обмеження. Ми потім покажемо, що час завершення для цього програмного використовуючого i пріоритетні переривання - фактично те ж чи ми застосовуємо обмеження або (не конструкцією ми знаємо, що час завершення, що користується j пріоритетними перериваннями, складає завжди 1), тобто коефіцієнт для екстремальної програми, отриманий таким чином, фактично тим же, що ми застосовуємо при обмеженні. Обмеження, можливо, збільшує час завершення, але ніколи не зменшує його. Ми запускаємо обговорення, яке приводитиме нас до екстремальної програми, використовуючи обмеження. Ми починаємо розглядати екстремального програмного P з обмеженням. Із-за обмеження, тільки рівень свободи, яку ми маємо, коли ми вирішуємо, як планувати програму - те, скільки з i пріоритетних переривань, які ми призначимо кожній групі процесорів Відколи ми є зацікавлено в порівнянні оптимальних графіків, ми звичайно призначимо i пріоритетні переривання групи c процесора в оптимальному шляху. Користуючись цим оптимальним призначенням, яке ми розглядаємо групу процесорів, яка містить процесор з найдовшим часом виконання, тобто група, яка обмежує час завершення повної програми. Без втрати загальності ми припускаємо, що це група 1, що містить m1 процесори, і j 1 = m 1 – 1 пріоритетні переривання, користуючись j пріоритетними перериваннями. У i-плануванні ми означимо число пріоритетних переривань в групі 1 i1. Із-за тимчасових плануючих обмежень ми можемо вважати групу 1 ізольованою від інших. Із попередніх результатів [2] ми знаємо, що екстремална (частина) програми P, яка виконується на групі 1, полягає в n 1 = m 1+ i 1+1 роботі рівної довжини m1 / n1. Проте, відколи ми розглядаємо оптимальне призначення пріоритетних переривань до процесора групи ми знаємо, що час завершення групового k зросте на ik – 1 таким чином, що це стає довшим (чи щонайменше, поки) час завершення групи 1, користуючись i1 пріоритетними перериваннями, тобто груповий k потім стане критичною частиною програми. Це означає, що, коли ik > 0 потім частина програмного P, який працює на груповому k, має бути екстремальною для пріоритетних переривань. Ми користуємося цим відкриттям нижче. Ми створюємо програму P', яка ідентична програмі P в групі 1. Ми до того ж розглядаємо точно такий же розподіл пріоритетного переривання серед груп в P', як і в P. В P' ми знаємо більше про процеси в інших групах, ніж в P, тому що ми також припускаємо, що груповий k має nk = mk + ik процеси, що мають ідентичний розмір в межах кожної групи. Тобто, ми припускаємо, що P' має ту ж структуру в усіх групах, як в групі 1. Ми потім показуємо, що від P, екстремальний, це слідує, що також P' екстремальний. Для цього нам треба показати, що поширення пріоритетного переривання є оптимальним бо P оптимальний також для P'. Тобто, якщо пріоритетні переривання поширюються по-іншому для P' час завершення не може бути нижче. Тепер зважаючи, коли ми в P' переміщають одно з ik пріоритетних переривань від група процесорів k до групи процесорів 1. Означимо час завершення для програмного P в груповому k by c (P, k),і ту ж кількість після пріоритетного переривання перемістив c' (P, k). Потім ми знаємо що c (P, 1) = c (P ′, 1) (P' і P ідентичні в групі 1), c ′(P, k)≤ c ′(P ′, k) ([2]), і c (P, 1)≤ c ′(P, k) (поширення пріоритетного переривання оптимальне для P). Отже c (P ′, 1)≤ c ′(P ′, k), так поширення пріоритетного переривання оптимальне також для P'. Отже, nk = mk + ik дійсний для усіх груп процесора в екстремальному програмному P' за винятком групи 1, де ми маємо. n 1 = m 1+ i 1+1, Це означає, що це там є Мається на увазі час завершення програмного P' не може бути меншим. Як наслідок, ми не можемо отримайте більше маленький час завершення для P' також, коли ми видаляємо обмеження. Починаючи з видалення обмеження, можливо, примушує час завершення бути нижче, це слідує, що програмний P' екстремальний також без обмеження. З моменту коли програма сконструйована, ми потім знаємо, що ми отримуємо час завершення с 2(m1 / n1), користуючись оптимальним графіком для i пріоритетних переривань, і що кількість праці в гурті 1 (m1 / n1) менша, довжина робіт у будь-якії іншії групі. Дві найменші роботи формують критичну опору, яка є змістом процесора тільки двох робіт, що неперервні. Проблема виявлення екстремальної програми - отже проблема виявлення програми з m + i +1 роботами, де дві найменші роботи такі великі як можливий, для присвоєння значень на м, j і i. 3.3. Формула для G (m, i, j) Робота з програмою P', як визначається вище, потрібна для того, щоб вичислити формулу. Маючи процесори м і роботи, ми можемо негайно сказати, що G (m, i, j)≤ 2 m ⁄(m + i +1)- середнє значення робіт розмірів (ми припускаємо, що час j-завершення P' складає 1), а дві найменші роботи формують критичну опору. Ми також знаємо, що усі роботи в тому ж i-кластері мають той же розмір. оптимальне значення більшості випадків, менше, ніж це. Припустимо, що оптимальний i-графік P' має c груп. Для того, щоб знайти найгірший випадок, нам треба поширювати роботи і процесори м на c групи. Це дає c коефіцієнти, m 1⁄ n 1,…, mc ⁄ nc де m 1+…+ mc = m і n 1+…+ nc = n. Ми зацікавлені в найменшому з цих коефіцієнтів: min (m 1⁄ n 1,…, mc ⁄ nc), які формують критичну точку в j-графіку. Якщо ми вибираємо поширення m 1, …, mc і n 1, …, nc таким чином, що цей мінімум максимальний, ми маємо «программу на йгіршого випадку». Отже Визначення 1. Мотивацією для цієї примітки є те, що вона має практичне застосування. У мінімумі min (m 1⁄ n 1,…, mc ⁄ nc), де m 1+…+ mc = m і, n 1+…+ nc = n шукаючи раціональну оцінку коефіцієнта м / n нижче. Коефіцієнт м / n розщеплений в c коефіцієнти, і більший c, більше незріла оцінка, яку ми отримуємо. Стартове значення - c = 1, де Повертаючись до багатопроцесорного контексту, потім ми пробуємо знайти значення c в Це означає, що кожна група має ще одну роботу між процесорами. Ці групи мають j - пріоритетні переривання поширювані серед i + 1 груп. Тоді найменші роботи настільки великі на скільки можливо, якщо групи є, відсортнованими порівну також наскільки можливо. Отже, деякі групи мають в i-графік. Така група містить роботи на відповідно, які дають в повному 2i + j + 2 робіт. Ми довели простішу формулу m ≥ i + j +1. Лема 3:, Якщо m ≥ i + j +1 ми маємо Якщо, m > i + j +1 деякі процесори містять невивантажені роботи в обох i - і j- графіках. Якщо м менше ніж, i + j +1 якщо m – j < i + 1, ми в j-графіку скорочують кількість з груп від i + 1 до м - j групи. Це дозволяє усім пріоритетним перериванням бути використаним який вимагає оптимальний графік. Починаючи з n = м + i + 1, тотожність Ми зараз можемо підсумовувати основний результат в теоремі, повторюючи Теорему 1 частина 2. Теорема 2: Для усього м >0 цілих чисел і 0 ≤ i < j, ми маємо: Алгоритм 1 - обчислюючи значення. 1. a ← m мод n іb ← n. 2. Ініціалізуйте: l ← 0, L ← 1, r ← 1, R ← 1, x ← b – a, y ← a. 3. Якщо c >max(x, y) потім 4. Якщо x = y потім 5. Якщо x < y виконують, l ← l + r L ← L + R y ← y – x, і прямують 3. 6. Якщо x > y виконують, r ← l + r R ← L + R x ← x – y, і прямують 3. 7. У Теоремі 3, ми імпортуємо від [12] алгоритм, який генерує усі кількості для c = 1,..., n, як векторний F. Припускають, що м і n не має ніякого загального множника. У [12] доведено, що
Рис.2 Дерево розщеплення Теорема 3:, Якщо m ⁄ n = k для деяких цілих k, то У алгоритмах, стрілка ← використана в трьох різних способах: 1. Якщо x – число x ← y, означає призначення значення y до мінливого x. 2.Якщо x – послідовність, А або B, p і p + 1 у векторному x. Векторний x має максимальний довжина n, так входи вставили після довжина c проігноровані. Отже, значення вправо від p у векторному x - усі juxtapositioned один крок управо, і довжина векторного x збільшена. 3. Якщо x - послідовність F, Алгоритм 2, частина 1 – конструювання 1. Нехай d=GCD(m,n). Приписаний m ← m ⁄ d і n ← n ⁄ d також приписаний m ← m мод n. 2. Ініціалізуйте: 3. Зробіть 4a., Якщо 4b., Якщо 4c., Якщо 5. p ← p + 1, g ← g – 1 і Вихід. Алгоритм 2, частина 2 – пошук 1. Алгоритм починається з цінностей, визначених Алгоритмом l, тобто: p, g від 5, d від l і A і B від 3. До того ж, ініціалізуйте як пара: F - порожня послідовність. Тоді x ← p – 1, u ← 1, q ← g. 2. q ← q – 1. Виберіть i таким чином, що B (i) = q. 3a., Якщо q = 0, 3b., Якщо i < p, 3c., Якщо i > p, u ← v + u. Прямують 2. 4. Якщо d > 1, копіюйте кожне значення в F в d копіює без заміни замовлення. Це збільшує довжину вектору чинником d. 5. Додайте 6. Складність алгоритму є O(n). Алгоритм 2 складається з двох окремих частин. Спершу ми конструюємо вихідну частку послідовнщсті Ми закінчуємо секцію коротким описом (Рис. 2) дерева Штерна-Боркота. Першу частина алгоритму конструює це дерево, і друга частина шукає назад в нім переходи. Це дерево повністю представляється в [8]. Близько воно може ітераційно бути сконструйований "Mediant (середнє) додавання": проводячи середні в міжсередніх інтервалах, ми отримаємо Відмітьте, що замовлення розміру збережене: усі послідовності зростають. Дерево сформоване приєднуючи до пов'язаних коефіцієнтів краями, і дозволяючи кожному породженню сформувати певний рівень у дереві. Це доводиться в [8] що усі ненегативні коефіцієнти відбуваються точно одного разу в дереві і з'являються завжди в найдовші терміни. Вище мивстановили доцільність кількості Висновки Вивантажуючи роботу і повторно запускаючи це на іншому процесорі, ми отримуємо швидше недорогі багатопроцесорні системи, як наприклад загальні мультипроцесори пам'яті. Це може, однак, з пріоритетного переривання може, проте, призвести до неурівноваженого завантаження в мультипроцесорі, навіть при користуванні кращим можливим непріоритетним графіком. Тому, є вибір з альтернативних варіантів між зменшенням числа пріоритетних переривань (і отже кількість накладних витрат) і збереженням завантаження розсудливого балансу між процесорами (чи комп'ютери) в системі. Наші результати роблять можливим точне визначення кількості одного основного елементу в максимальній Продуктивності та вигоді, збільшуючи число пріоритетних переривань. Результати легко обчислити також для масивно паралельного мультипроцесора, тобто, якщо м дуже великий. Обговорення Наші результати узагальнюють результати Braun і Schmidt [2]. Вони дивляться на вигоду максимальної продуктивності, представлення m – i –1 нових пріоритетних переривань в графіку з i пріоритетними переривання, працюючі на системі з м процесорами (комп'ютери). Ми надаємо основну формулу, яка обчислює максимальну вигоду представлення додаткових j пріоритетних переривань у графіку з i пріоритетними перериваннями, користуючись процесорами м. Наприклад, отримання максимальної користі, якщо ми представляємо одно додаткове пріоритетне переривання в графіку з одним пріоритетним перериванням користування м процесорами яке може бути вичислене. (Рис.3 і 4) за відображають функцію G з i - проти j-переривань робочого інтервалу програми «найгіршого випадку» для м = 200 відповідного м = 400. Якщо i ≥ j значення з G тривіально дорівнює одному. Це може бачитися як низька плоска область в зображеннях. Для m ≥ i + j +1 ми можемо представити формулу як формулу з функціями (див. вище Лема 3), тому значення G постійне для усіх j з k (i + 1)≤ j ≤ k (2(i + 1)– 1), k ∈ N. Це пояснює частину з зображень, що має форму трикутника/ плато. Наприклад, для м = 200 і i = 50 значення G = 1.333 для 50 ≤ j ≤ 98. Те ж значення G складає для i = 10 і 10 ≤ j ≤ 18. Це означає, що вигода зі збільшення числа пріоритетних переривань з 50 до 55, або з 50 до 98, або навіть від 10 до 18 - те ж, припускаючи, що немає ніяких накладних витрат. Бо для m < i + j ми маємо формулу «дерева» Stern-Brocot:
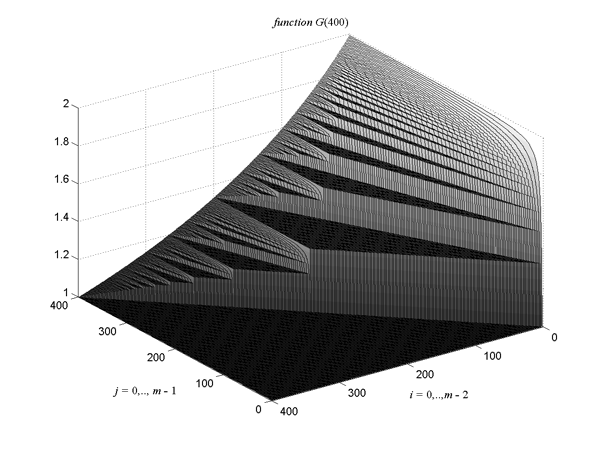
Мал. 3 Функція G при m=200
Мал. 4 Функція G при m=400 Список літератури 1. Blazewicz, J., Ecker, K. H., Pesch, E., Schmidt, G., Weglarz, J., Scheduling Computer and Manufacturing Processes, Springer Verlag, New York, NY 1996, (II ed.) 2. Braun, O., Schmidt, G., Parallel Processor Scheduling with Limited Number of Preemptions, Siam Journal of Computing, Vol. 32, No. 3, 2003, pp. 671-680 3. Coffman Jr., E. G., Garey, M. R., Proof of the 4/3 Conjecture for Preemptive vs. Nonpreemptive Two-Processor Scheduling, Journal of the ACM, Vol. 40, No. 5, November 1993, pp. 991-1018, ISSN:0004-5411 4. Dobrin, R., Fohler, G., Reducing the Number of Preemptions in Fixed Priority Scheduling, in Proceedings of the 16th Euromicro International Conference on Real-Time Systems, ECRTS 04, Catania, Sicily, Italy, June 2004 5. Garey, M. R. and Johnson, D. S., Computers and Intractability - A Guide to the Theory of NP-Completeness, W. H. Freeman and Company, New York, 1979 6. Graham, R. L., Bounds for Certain Multiprocessing Anomalies, Bell System Technical Journal, Vol. 45, No. 9, November 1966, pp.1563-1581 7. Graham, R. L., Bounds on Multiprocessing Timing Anomalies, SIAM Journal of Applied Mathematics, Vol. 17, No. 2, 1969, pp. 416-429 8. Graham, R. L., Knuth, D., Patashnik, O., Concrete Mathematics, Addison-Wesley, ISBN 0-201-14236-8, 1994 9. Karger, D., Stein, C., Wein, J., Scheduling Algorithms, in Handbook of Algorithms and Theory of Computation, M. J. Atallah, editor. CRC Press, 1997 10. Lawler, E. G., Lenstra, J. K., Rinnooy Kan A. H. G., Shmoys, D. B., Sequencing and Scheduling: Algorithms and Complexity, S.C. Graves et al., Eds., Handbooks in Operations Research and Management Science, Vol. 4, Chapter 9, Elsevier, Amsterdam, 1993, Chapter 9, pp. 445-522 11. Lennerstad, L., Lundberg, L., Optimal Scheduling Combinatorics, Electronic Notes in Discrete Mathematics, Vol. 14, Elsevier, May 2003 12. Lennerstad, H., Lundberg, L., Generalizations of the Floor and Ceiling Functions Using the Stern-Brocot Tree, Research Report No. 2006:02, Blekinge Institute of Technology, Karlskrona 2006 13. Liu, C. L., Optimal Scheduling on Multiprocessor Computing Systems, in Proceedings of the 13th Annual Symposium on Switching and Automata Theory, IEEE Computer Society, Los Alamitos, CA, 1972, pp. 155-160 14. McNaughton, R., Scheduling with Deadlines and Loss Functions. Management Science, 6, 1959, pp. 1-12 15. Pinedo, M., Scheduling: Theory, Algorithms and Systems, (2nd Edition), Prentice Hall; 2 edition, 2001, ISBN 0-13-028138-7 Стаття III
|
||
|
Последнее изменение этой страницы: 2016-06-22; просмотров: 336; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.011 с.) |

 якщо m ≥ i + j +1 формула може також бути записана, як
якщо m ≥ i + j +1 формула може також бути записана, як 
 може бути певним комбінаторним або деревовидним (Stern-Brocot розділ 3). Це також може вичислити алгоритм, який має лінійну складність (теорема 3), який отже також належить до основних результатів. Це - специфічна раціональна оцінка від нижче m / n кофефіцієнта, який знаходиться в закритому інтервалі.
може бути певним комбінаторним або деревовидним (Stern-Brocot розділ 3). Це також може вичислити алгоритм, який має лінійну складність (теорема 3), який отже також належить до основних результатів. Це - специфічна раціональна оцінка від нижче m / n кофефіцієнта, який знаходиться в закритому інтервалі. 
 роботи в екстремальній програмі.
роботи в екстремальній програмі.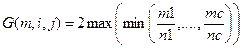 де максимум прийнятий усю безліч цілих чисел m 1, …, mc і n 1, …, nc де усе mk > 0 і nk ≥ 0 інший, і число групи c залишаються, щоб бути вказаним. Також, важливо знайти, що ефективний алгоритм обчислює цю кількість. Цьому було приділено увагу в [12]. Стаття описує алгоритм, який є O (мах (n, m)), тобто це має у більшості лінійну складність в n і м. Наступна примітка нам показує:
де максимум прийнятий усю безліч цілих чисел m 1, …, mc і n 1, …, nc де усе mk > 0 і nk ≥ 0 інший, і число групи c залишаються, щоб бути вказаним. Також, важливо знайти, що ефективний алгоритм обчислює цю кількість. Цьому було приділено увагу в [12]. Стаття описує алгоритм, який є O (мах (n, m)), тобто це має у більшості лінійну складність в n і м. Наступна примітка нам показує: ,де максимум взятий зпоміж цілих чисел m 1, …, mc і n 1, …, nc таким чином m 1 + … + mc = m, n 1 + … + nc = n всі mk > 0і nk ≥ 0 і
,де максимум взятий зпоміж цілих чисел m 1, …, mc і n 1, …, nc таким чином m 1 + … + mc = m, n 1 + … + nc = n всі mk > 0і nk ≥ 0 і , а потім
, а потім  не зменшується аж поки значення c = n, де залишок - ціле число, над функцією:
не зменшується аж поки значення c = n, де залишок - ціле число, над функцією: 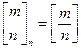 . Ми не записуємо кількість
. Ми не записуємо кількість  відколи
відколи  взагалі.
взагалі. пріоритетні переривання, і інші мають
пріоритетні переривання, і інші мають  пріоритетних переривань. Ці i + 1 група містять
пріоритетних переривань. Ці i + 1 група містять  або
або  процесори, відповідно. Підсумовуючи число процесорів групи дають в повному j + i + 1 процесор, ми тепер розглядаємо випадок групи з
процесори, відповідно. Підсумовуючи число процесорів групи дають в повному j + i + 1 процесор, ми тепер розглядаємо випадок групи з 
 роботи
роботи
 потім дає
потім дає 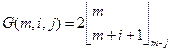 ,
, . Якщо m ≥ i + j +1, формула може також бути записана як
. Якщо m ≥ i + j +1, формула може також бути записана як  . Значення
. Значення  може бути вичислене наступним алгоритмом. Тут x ← y має значення призначення значення y до змінного x.
може бути вичислене наступним алгоритмом. Тут x ← y має значення призначення значення y до змінного x. і прямують 7.
і прямують 7. іпрямують 7.
іпрямують 7. .
. , створено з пар розкладаючи коефіцієнт обоє, який належить до останньої генерації. Це може бути ітеровано подальшими c – 2 кроками, для отримання
, створено з пар розкладаючи коефіцієнт обоє, який належить до останньої генерації. Це може бути ітеровано подальшими c – 2 кроками, для отримання 
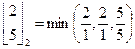 і
і  «Штерна-Беркота
«Штерна-Беркота . Інакше послідовність
. Інакше послідовність  обчислюється наступними двома алгоритмами.
обчислюється наступними двома алгоритмами. має на увазі вставку значення y між позиціями
має на увазі вставку значення y між позиціями мається на увазі додавання в кінець i копій значення y після витримки позиція в x. Довжина вектору отже зростає i.
мається на увазі додавання в кінець i копій значення y після витримки позиція в x. Довжина вектору отже зростає i.
 , B = (0, 1), l ← 0, L ← 1, r ← 1, R ← 1, g = 2, p = 1.
, B = (0, 1), l ← 0, L ← 1, r ← 1, R ← 1, g = 2, p = 1. , і
, і 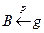 , і g ← g + 1 і прямують відповідного випадку 4a, 4b або 4c.
, і g ← g + 1 і прямують відповідного випадку 4a, 4b або 4c. , виходять з повторення і прямують 5.
, виходять з повторення і прямують 5. , виконуює r ← l + r і R ← L + R і прямують 3.
, виконуює r ← l + r і R ← L + R і прямують 3. , виконують l ← l + r, L ← L + R і і прямують 3.
, виконують l ← l + r, L ← L + R і і прямують 3. i
i і виходять з повторення, тобто прямують 4.
і виходять з повторення, тобто прямують 4. , x ← x – 1, v ← v + u. Прямують 2.
, x ← x – 1, v ← v + u. Прямують 2. , де
, де  .
. . породження В другому алгоритм ми працюємо в зворотному напрямку вихідної послідовності, щоб сконструювати відповідні С-значення і послідовності
. породження В другому алгоритм ми працюємо в зворотному напрямку вихідної послідовності, щоб сконструювати відповідні С-значення і послідовності  . Починаючи з послідовності коефіцієнта
. Починаючи з послідовності коефіцієнта  і
і , що йде за
, що йде за  і,
і,  і так далі, в кожному кроці, що додає нове покоління коефіцієнтів.
і так далі, в кожному кроці, що додає нове покоління коефіцієнтів. . Для j = m – 1 та i = 0, …, m – 2 крива представляє результати Braun і Schmidt [2]
. Для j = m – 1 та i = 0, …, m – 2 крива представляє результати Braun і Schmidt [2]