
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Наваньаження компенсації ланцюгамиСодержание книги
Поиск на нашем сайте
Як обговорюється, кожна послідовність (r 1, …, rn – 1) визначає n – 1 ланцюги: Ci ={ r 1+…+ ri, r 2+…+ ri,…, ri } i = 1, …, n – 1. Давайте розглядати найбільш завантажений комп'ютер. Якщо ми, наприклад, вибирають три ланцюги Ci 1, Ci 1 і, Ci 3 це вимагатиме Очевидно, якщо списки не перетинаються, таким чином Взагалі ми маємо наступне: Теорема 1: Нехай I = { i 1, …, is } (для s > 0), є певною к−тю процесів, якими усі є переміщено в комп'ютер y, якщо усі комп'ютери в Доказ: Взагалі, множина Знаходяться в повних можливих об'єднаннях 2 n – 1 – 1 великих кількостей C 1, …, Cn – 1, які Ми позначаємо об'єднанням близько, тоді як описують, кожне об'єднання має дві властивості, які цікаві для наших цілей. Ми, можемо, пере формулювати визначення в термінах розміру і числа великих кількостей:
Від об'єднань хоча i = 1, …, min(k, l) і k – l =1. Порожня послідовність – корінь у дереві, і усі схеми відновлення − листи. Ми називаємо це дерево деревом послідовності (подивіться Мал. 3).
Мал. 3 Приклад дерева послідовностей для n = 5 В принципі, нам треба розслідувати усі можливі об'єднання для кожної з послідовності. Проте, є декілька шляхів виключити великі множини послідовності і об'єднання. Наступна анотація дає умову з низькою складністю це категоризує великий клас послідовностей як неоптимальний. Анотація уперше вимагає визначення. Визначення 3. Ми говоримо, що BVщільна аж до q, якщо є схема відновлення R таким чином L (n, i, R) = BV (i) для i = 1, …, q. Анотація 2: Припускають, що BV щільна аж до q. Потім усі часткові суми r аж до потреби BV (q) є чітким, якщо R − n−оптимальна схема відновлення. Іншими словами Доказ: Припускають протиріччя, тобто, що дві часткові суми однакові, скажемо в ряду i і j. Припускають, що i ≥ j. Потім ми повинні i (i + 1)⁄ 2 – 1 того, як вимкнення отримають процеси на комп'ютері з найважчим навантаженням. Це суперечить оптимальності R. Це означає, що ми можемо почати із заздалегідь розрахованих модульних послідовностей (дивляться [17]). Ми говоримо, що такі послідовності задовольняють модульну умову. Якщо модульна послідовність має чіткі послідовності аж до номерів м в послідовності, ці номери початкової букви m може бути використані як початок послідовності, і залишається (n – m –1)! Послідовність для знаходження оптимальності. 6. Напруженість MV Ми тут розслідуємо для якого значення n і q, зв’язаного MV є щільний. Щільна межа під назвою SV. Напруженість MV, витікає із заздалегідь зробленої послідовності. Отже, якщо ми маємо одну схему відновлення, яка йде за MV аж до q, ми можемо відкинути усі схеми відновлення, де не усі часткові суми аж до q чіткі. Наступний алгоритм знаходить усі послідовно оптимальні схеми відновлення. Якщо попередня послідовність, яка має p-оптимальність, ми негайно можемо відмінити дослідження з послідовності, яка не має p-оптимальність. Також повна гілка дерева послідовності, гілка, яка має ідентичну голвну послідовність, може бути переміщена. Це наслідок послідовного балансування навантаження. До того ж, Анотацією 2 і модульною умовою, великий клас неоптимальної послідовності, переміщений. Якщо знаходять, що послідовність не оптимальна, пошук триває у сусідній гілці.
Алгоритм У алгоритмі, послідовності А і B належать до множини усіх можливих перестановок з цілочисельних номерів з 1 до n, якиі виконують умову (подивіться Анотацію 2) модуля. Нехай pd (A) = min { pj: 1. Нехай є послідовністю, яка задовольняє умову модуля, і обчислюють pd (A)< pd (B) для усіх d = 1 ,..., n − 1; 2. while (the set of remaining sequences satisfying the modulo condition is non−empty) Do begin 3. Let B be a sequence that satisfies the modulo conditions that not yet has been considered; 4. Let d = 1; 5. while d < n do begin a) if pd(A) < pd(B) then begin break and goto 2); // B відмінене end; b) if pd(A) = pd(B) then begin d = d +1; // перевірка наступної глибини goto 5) if pd(A) > pd(B) then begin A = B; // A є відмінене calculate pd(A) < pd(B) for all d = 1 ,..., n − 1; break and goto 2); end; end; end; 6. SV = < p1(A), p2(A),..., pn− 1(A)>, де SV − оптимальний вектор послідовності. Малюнки нижче (Мал. 4, 5 і 6) показують відношення між MV вектором межі і оптимальним вектором SV для n дорівнюють 10, 15 і 20. Для нижчого ряду вимкнень MV вектор межі щільний, але не для більшого номера. Наприклад, для MV щільний аж до семи вимкнень (Мал. 4). Для восьми вимкнень різниця між MV і SV одна. Це означає, що не існує схеми відновлення для десяти комп'ютерів з поведінкою як MV для будь-якого числа вимкнень аж до восьми вимкнень. У розподіленій системі з 15 комп'ютерами (Мал. 5) пов'язана MV щільна аж до восьми вимкненьи. Дивно, MV не щільна для дев'яти вимкнень, але щільнадля десяти вимкненьи. Для 20 комп'ютерів в розподіленій системі межа щільна аж до тринадцяти вимкнень (Мал. 6). пов'язана MV тривіально щільна, коли комп'ютери вимикається (d = n − 1). Потім усі процеси знаходяться в одному комп'ютері.
Мал. 4 SV вектор проти MV вектора для n = 10
Мал. 5 SV вектор проти MV вектора для n = 15
Мал. 6 SV вектор проти MV вектора для n = 20
Щоб показати відмінності між MV і SV, ми уперше подали діаграму векторів межі MV (подивіться Мал. 7) для розподілених систем, що включають аж до 21 комп'ютера. Малюнок подає навантаження на найбільш завантаженому комп'ютері, коли q комп'ютери в розподіленій системі вимкнені.
Мал. 7 Межа векторів MV до 21 комп’ютера в розподіленій системі У Мал. 8 ми подали мінімальне навантаження на найбільш завантаженому комп'ютері для різного номера комп'ютерів, які вимикається, тобто вектори SV.
Мал. 8 Вектори SV до 21 комп’ютера в розподіленій системі
Мал. 9 демонструє представлення різниць між SV і MV для усіх n аж до 21. Для пов'язаної MV щільної для будь-якого числа вимкнень (ми розглядаємо максимум n − 1 ушкоджень). Число максимуму пошкоджених комп'ютерів, де SV співпадають з MV представлений у Таб. 2. Таблиця показує також приклади птимальних послідовностей. Мал. 10 показує, до яких MV протяжностей щільна. У сірій MV області щільна, починаючи з MV = SV. Для більших значень пошкоджених комп'ютерів q, MV < SV, так MV не щільна. Це область така ж як область в Мал. 8, де різниця між MV і SV нульова. З цього слідує, що область не може бути крім того розширена. Лінія на малюнку – результат кращої послідовності модуля були присутніми в [17].
Мал. 9 Представлення різниці SV та MV для n від 1 до 20
Мал. 10 Порівняння послідовностей оптимальної схеми відновлення з модульними послідовностями
Обговорення і укладення У багатьох розподілених системах і кластерах, проектувальник повинен забезпечити схеми відновлення. Такі схеми визначають, як треба перерозподілити робоче навантаження, коли один або більше комп'ютерів вимикається. Мета − тримати навантаження, якомога рівномірніше розподіленим між усіма комп’ютерами, навіть, коли самі несприятливі комбінації комп'ютерів вимикаються. Це особливо важливо в системах реального часу. Техніка толерантності до апаратних помилок може ділитися на дефектоскопію і толерантність помилці [24]. Різна техніка використана, щоб дослідити дефектоскопію і є широке дослідження в цій області (наприклад [4,21,25,31]). Задача дефектоскопії є за межами можливості цієї статті.
Таб. 2 Оптимальні множини Ми розглядаємо n ідентичні комп'ютери, які виконують один процес кожен. Усі процеси виконують ту ж кількість роботи. Схеми відновлення, які гарантують оптимальний найгірщий випадок поширення навантаження, коли x комп'ютери вимкнулися, названі схемами оптимального відновленням для значення n і x. У цій статті ми подали алгоритм, який дає оптимальні схеми відновлення для будь-якого числа вимкнень. Складність алгоритму є показова функція. Для оптимальних схем відновлення вичислено аж до 21 комп'ютера. Ми також порівнюємо результати до заздалегідь представленої нижчої межі MV [20]. Результати показують, що для аж до дев'яти комп'ютерів, MV =SV для будь-якого числа вимкнених комп'ютерів, так в цьому інтервалі MV щільна. Для більш ніж дев'ять число комп'ютерів, MV щільна тільки, коли декілька чисел комп'ютерів вимкнені. Порівняння з результатами в [17], виконання різниці, що виражається різницею між SV і MV, більша, ніж очікується. Ця стаття забезпечує вичерпне рішення заздалегідь проблемного формулювання статики толерантності до помилки. Оптимальні послідовності обчислені, тобто послідовності, які дають оптимальний навантаження поширення для будь-якого числа пошкоджених комп'ютерів. Проблемне формулювання саме природнє для сценарію схем статичного відновлення. Для того, щоб користуватися цими схемами, один повинен мати деякий механізм для виявлення, коли комп'ютери несправні. Це може бути зроблене в різні способи, наприклад, користуючись пульсацією або жвавістю ланцюгів [24] чи звичайними перервами в цьому випадку зовнішні системи живлення даними всередині вузла в кластері. Виявленням відмови часто управляє кластерне програмне забезпечення, і оптимальні схеми відновлення можуть в тих випадках бути безпосередньо використаним в nodelist в Sun Cluster [17], список пріорітетів MC/ServiceGuard (HP) [5], каскадна група в HACMP (IBM) [6], і лист представлення в Windows Server 2003 clusters (Microsoft, earlier called MSCS)[22]. Є уповільнення, викликане накладними витратами, зв'язане з перезарядкою задачі (обробки) на новому вузлі після відмови. Факт, що ми користуємося статичними схеми відновлення може до деякої міри зменшити цю задачу. Користуючись статичними схемами, ми знаємо, на якому комп'ютері в процесі треба буде знову почати список відновлень продовжуючи розмноження поточного стану процесу до наступного вузла в ланцюзі, і отже приводячи час для перезарядки процесу у разі відмови. Це не можливо, коли ми користуємося динамічними схемами, у такому разі ми не знаємо, на якому вузлі процес треба знову почати. Список літератури 1. Bertsekas, D.P., Ozveren, C., Stamoulis, G.D., Tsitsiklis, J.N., Optimal Communication Algorithms for Hypercubes, Journal of Parallel and Distributed Computing, 11, 1991, pp. 263−275 2. Bloom, G. S., Golomb, S. W., Applications of Numbered, Undirected Graphs, Proceedings of the IEEE, 65(4), 1977, pp. 562−571 3. Chabridon, S., Gelenbe, E.: Failure Detection Algorithms for a Reliable Execution of Parallel Programs, in Proceedings of 14th Symposium on Reliable Distributed Systems SRDS'14, Bad Neuenahr, Germany, September 1995 4. Chinchani, R., Upadhyaya, S., Kwiat, K., A Tamper−Resistant Framework for Unambiguous Detection of Attacks in User Space Using Process Monitors, in Proceedings of First IEEE International Workshop on Information Assurance IWIA'03, March 24−24, 2003, Darmstadt, Germany, pp. 25−36 5. Cristian, F., Understanding Fault Tolerant Distributed System s, Communication of the ACM, 34(2), 1991, pp. 56−78 6. Dimitromanolakis, A, Analysis of the Golomb Ruler and the Sidon Set Problems, and Determination of large, near−optimal Golomb Rulers, Dept. of Electronic and Computer Engineering Technical University of Crete, June, 2002 7. Gelenbe, E., A Model for Roll−back Recovery With Multiple Checkpoints, in Proceedings of 2nd International Conference on Software Engineering, San Francisco, California, US, October 1976, pp. 251−255 8. Gelenbe, E., Chabridon, S., Dependable Execution of Distributed Programs, Elsevier, Simulation Practice and Theory, 3(1), 1995, pp. 1−16 9. Gelenbe, E., Derochete, D., Performance of Rollback Recovery Systems under Intermittent Failures, Communication of the ACM, 21(6), 1978, pp. 493−499 10. Greenberg, D. S., Bhatt, S. N., Routing multiple paths in hypercubes, in Proceedings of Second Annual ACM Symposium on Parallel Algorithms and Architectures, Island of Crete, Greece, 1990, pp. 45 – 54 11. Hewlett−Packard Company, TruCluster Server − Cluster Highly Available Applications, Hewlett−Packard Company, September 2002 12. Hewlett−Packard, Managing MC/ServiceGuard, Hewlett−Packard, March 2002 13. Huang, C., McKinley, P. K., Communication Issues in Parallel Computing across ATM Networks, IEEE Parallel and Distributed Technology: Systems and Applications, 2(4), 1994, pp. 73−86 14. IBM. HACMP, Concepts and Facilities Guide, IBM, July 2002 15. Kameda, H., Fathy, E.−Z.S., Ryu, I., Li, J., A performance Comparison of Dynamic vs. Static Load Balancing Policies in a Mainframe − Personal Computer Network Model, Information: an International Journal, 5(4), 2002, pp. 431−446 16. Klonowska, K., Lundberg, L., Lennerstad, H.: Using Golomb Rulers for Optimal Recovery Schemes in Fault Tolerant Distributed Computing, in Proceedings of 17th International Parallel & Distributed Processing Symposium IPDPS 2003, Nice, France, April 2003, pp. 213, CD−ROM 17. Klonowska, K., Lundberg, L., Lennerstad, H., Svahnberg, C.: Using Modulo Rulers for Optimal Recovery Schemes in Distributed Computing, in Proceedings of 10th International Symposium PRDC 2004, Papeete, Tahiti, French Polynesia, March 2004, pp. 133−142 18. Krishna, C.M., Shin, K.G., Real−Time Systems, McGraw−Hill International Editions, Computer Science Series, 1997, ISBN 0−07−114243−6 19. Lundberg, L., Haggander, D., Klonowska, K., Svahnberg, C., Recovery Schemes for High Availability and High Performance Distributed Real−Time Computing, in Proceedings of 17th International Parallel & Distributed Processing Symposium IPDPS 2003, Nice, France, April 2003, pp. 122, CD−ROM 20. Lundberg, L., Svahnberg, C., Optimal Recovery Schemes for High−Availability Cluster and Distributed Computing, Journal of Parallel and Distributed Computing, 61(11), 2001, pp. 1680−1691 21. Mahmood, A., McCluskey, E.J., Concurrent Error Detection Using Watchdog Processors − A Survey, IEEE Transactions on Computers, 37(2), 1988, pp. 160−174 22. Microsoft Corporation, Server Clusters: Architecture Overview for Windows Server 2003, Microsoft Corporation, March 2003 23. Pande, S.S., Agrawal, D.P., Mauney, J., A threshold scheduling strategy for Sisal on distributed memory machines, Journal on Parallel and Distributed Computing, 21(2), 1994, pp. 223−236 24. Pfister, G.F., In Search of Clusters, Prentice−Hall, 1998 25. Reinhardt, S.K., Mukherjee, S.S., Transient Fault Detection via Simultaneous Multithreading, in Proceedings of 27th Annual International Symposium on Computer Architecture (ISCA), Vancouver, British Columbia, Canada, June, 2000 26. Stalling, W., Computer Organization & Architecture, Designing for Performance, Sixth Edition, Prentice Hall, 2003, ISBN 0−13−049307−4 27. Sun Microsystems. Sun Cluster 3.0 Data Services Installation and Configuration Guide, Sun Microsystems, 2000 28. TruCluster, Systems Administration Guide, Digital Equipment Corporation, http:// www.unix.digital.com/faqs/publications/cluster_doc 29. Vaidya, N.H., Another Two−Level Failure Recovery Scheme: Performance Impact of Checkpoint Placement and Checkpoint Latency, Technical Report 94−068, Department of Computer Science, Texas A&M University, December 1994 30. Willebeek−LeMair, M., Reeves, A.P., Strategies for Dynamic Load Balancing on Highly Parallel Computers, IEEE Transactions on Parallel and Distributed Systems, 9(4), 1993, pp. 979−993 31. Young, M., Taylor, R.N., Rethinking the Taxonomy of Fault Detection Techniques, in Proceedings of International Conference Software Enginering (ICSE), ACM, May, 1989, pp. 53−62 32. http://www.distributed.net/ogr/index.html 33. http://www.research.ibm.com/people/s/shearer/grtab.html
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-22; просмотров: 273; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.255.170 (0.008 с.) |

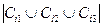 , щоб вимкнені процеси yi 1, 1, yi 2, 1 і yi 3, 1 комп'ютері y (подивіться Секцію 5.1), отримали аварією усіх комп'ютерів в списках Ci 1, Ci 1 і, Ci 3.
, щоб вимкнені процеси yi 1, 1, yi 2, 1 і yi 3, 1 комп'ютері y (подивіться Секцію 5.1), отримали аварією усіх комп'ютерів в списках Ci 1, Ci 1 і, Ci 3. , що не є таким, що не перетинає об'єднання, є деякі комп'ютери, чиї вимкнення дають багаторазовий ефект в передачі процесів до y, і число вимкнень, потрібних, більше меньше. Отже, після
, що не є таким, що не перетинає об'єднання, є деякі комп'ютери, чиї вимкнення дають багаторазовий ефект в передачі процесів до y, і число вимкнень, потрібних, більше меньше. Отже, після  вимкнені. Для схеми відновлення R і якщо p вимкнення відбуваються, ми маємо
вимкнені. Для схеми відновлення R і якщо p вимкнення відбуваються, ми маємо  .
. відповідає випадку
відповідає випадку  . Потім ми маємо процеси на тому ж комп'ютері. Ми потім перефразовуємо задачу заради алгоритму.
. Потім ми маємо процеси на тому ж комп'ютері. Ми потім перефразовуємо задачу заради алгоритму. .
.
 , номери для усіх а і b 1 ≤ a ≤ b ≤ BV (q), чіткі.
, номери для усіх а і b 1 ≤ a ≤ b ≤ BV (q), чіткі. Uj } для усього об'єднання Uj з глибина d (глибина – номер з множин в об'єднанні).
Uj } для усього об'єднання Uj з глибина d (глибина – номер з множин в об'єднанні).









