
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Додаток: Оптимальні ПослідовностіСодержание книги
Поиск на нашем сайте
У Таблиці 3 ми подали Оптимальні Лінійки Голомбо для n = 22 (відомо як n = 23, якщо ми рахуємо нуль)., m кількості − число не еквівалентних лінійці довжин послідовностей. Цікаво бачити, що для n = 4 і n = 10 ми маємо два OGRs, для n = 5 ми маємо чотири OGRs, і для n = 6 ми маємо п'ять OGRs [3,4,6,17,19]
Стаття IV Використання Лінійки Модуля для Схем Оптимального Відновлення в розподелених обчисленнях
Kamilla Klonowska, Lars Lundberg, Hakan Lennerstad, Charlie Svahnberg Proceedings of the 10th International Symposium PRDC 2004, Papeete, Tahiti, French Polynesia, March 2004
Резюме Кластери і розподілені системи дозволяють толерантність до помилок і високу продуктивність через спільне використання навантаження. Коли усі комп'ютери працюють, ми захотіли б розподілити навантаження порівну серед комп'ютерів. Коли один або більше комп'ютерів ламаються навантаження на цих комп'ютерах має бути перерозподілене на інші комп'ютери в кластері. Перерозподіл визначає схема відновлення. Схема відновлення повинна тримати навантаження, як найоптимальніше, коли вимикаються навіть несприятливікомбінації комп'ютерів, тобто ми хочемо оптимізувати поведінку найгіршого випадку. У цій статті ми визначаємо схеми відновлення, які оптимальні для більшого ряду вимкнених комп'ютерів, ніж в попередніх результатах. Ми також показуємо задачу виявлення оптимальної схеми відновлення, для кластеру з n комп'ютерами що відповідає математичній задачі виявлення щонайдовшої послідовності додатніх цілих чисел, для яких сума послідовністі і сума усього модуля послідовностей n унікальні. Ключові слова: толерантність до помилки, високе представлення обчислення, схеми відновлення, Лінійка Голомбо, модульна послідовність Вступ Один шлях отримання високої придатності і толерантністі до помилки − виконання додатку на кластерній або розподіленій системі. Є головний комп'ютер, який виконує додаток за нормальних умов і вторинний комп'ютер, який приймає завдання, коли головний комп'ютер вимкнений. Можливо, також є третій комп'ютер, який приймає завдання коли головний і вторинний комп'ютери − не працюють, і так далі. Порядок в якому комп'ютери використані названий пордком відновлення, заданим списком відновлення. Перевага користування кластерами, окрім толерантності до помилок, − навантаження, розподілене між комп'ютерами. Коли усі комп'ютери працюють, ми захотіли б, щоб навантаження було розподілене порівну. Навантаження на деяких комп'ютерах буде, зростати, коли один або більше комп'ютерів вимикаються, але і за цих умов, ми захотіли б розподілити навантаження як можна порівну на комп'ютерах, що залишилися. Поширення навантаження, коли комп'ютер вимкнений вирішене порядком відновлення процесів, що виконувалися на дефолтному комп'ютері. Сукупність усіх порядків відновлення є так званою схемою відновлення. Отже поширення навантаження повністю визначається схемою відновлення незважаючи на число комп'ютерів, що вимикаються. Ми розглядаємо схеми відновлення, що складаються із списків відновлень тієї ж структури у сенсі, що один список отримує додавання 1 до входів в попередній список модуля числа комп'ютерів (n). Це може розглядатися, як, комп'ютери сполучені в кільце, і певна схема відновлення відповідає певній множині стрибків між комп'ютерами. Стрибки ті ж, де б ми не починали. Ми користуємося терміном “обгортка по колу", коли загальна сума стрибків для процесу перевищує число комп'ютерів. Задача виявлення оптимальних (чи навіть кращих) схем відновлення не вивчалася до цього [6]. Схема цієї задачі представляється на мал.1. Перше математичне проблемне формулювання не включає циклічні "переходи". Ці схеми відновлення представляються в деталях в [5] і [6]. "Log" алгоритм є оптимальною схемою відновлення, де найбільше комп'ютерів вимикається в кластері з n комп'ютерів [6]. Тут "оптимальні" рішення − максимальне число процесів на одному комп'ютері після k дій − BV (k). Функція BV(k) забезпечує нижню межу для будь-якої схеми (подивіться [6] і Секція 3) відновлення. "Ощадлива" і схеми "Голомбо" (представляється в [5]) оптимальні для більшого ряду комп'ютерів, ніж "Log". Схеми Голомбо дають оптимальне рішення для більшого ряду вимкнених комп'ютерів, ніж Ощадлива схема. Обоє розглядають формулювання, де "обгортка по колу" не узята до розгляду. У цій статті ми оптимізуємо також, випадок коли "обгортка по колу" відбувається. Це математичний хід формулювання комп'ютерної постановочної задачі, і дає нову схему відновлення, названу модульною схемою, вона оптимальна для більшого ряду вимкнених комп'ютерів в оригінальній комп'ютерній постановочній задачі. Тобто ці результати представляють становище мистецтва в полях.
Мал. 1 Схема формулювання проблеми
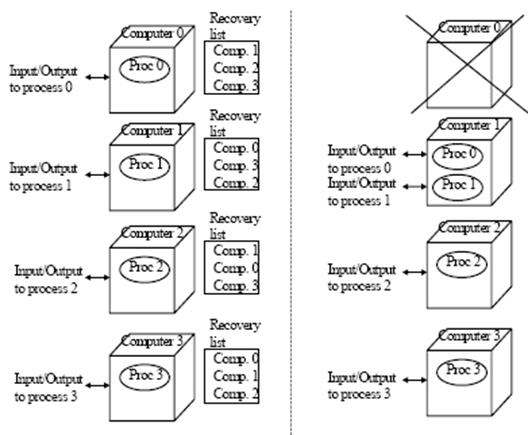
Формулювання задачі Ми розглядаємо кластер з n ідентичними комп'ютерами з одним процесом на кожному комп'ютері. Робота − рівномірно розділена між цими n процесами. Є асоційований список відновлень з кожним процесом. Цей список визначає, де процес треба знову почати, якщо поточні комп'ютери вимкнені. Сукупність усіх списків відновлень названа схемою відновлення. Мал. 2 показує таку систему для n = 4. Ми припускаємо, що процеси переміщаються назад, як тільки комп'ютер повертається знову. У найбільших кластерних системах це може розмістити користувач [3,9,10], тобто в деяких випадках один, можливо, не хоче автоматичного перерозподілу процесів, коли помилковий комп'ютер повертається знову. Ліва сторона малюнку показує систему за нормальних умов. В цьому випадку, є один процес на кожному комп'ютері. Списки відновлень також показані; один список для кожного процесу. Сукупність усіх списків відновлень названа схемою відновлення. Лицьова сторона мал.2 показує сценарій, коли комп'ютер нуль вимкнений. Список відновлень для процесу нуль показує, що його треба знову почати на комп'ютері один, коли комп’ютер нуль зламаний. Якщо комп'ютер один також зламаний, процес нуль буде знову розпочатий на комп'ютері два, який є другим комп'ютером в списку відновлень. Перший комп'ютер в списоку відновлень для процесу один − комп’ютер нуль. Проте, відколи комп’ютер нуль ламається процес один буде знову розпочатий на комп'ютері три. Тому, якщо комп'ютери нуль і один вимикаються, є два процеси на комп'ютері два (процес нуль і два) і два процеси на комп'ютері три (процеси одині і три). Якщо комп'ютери нуль і один зламані, максимальне навантаження на кожному з комп'ютерів, що залишилися, − двічі більше за нормальний стан. Це добрий результат, оскільки навантаження розділене порівну. Проте якщо комп'ютер нуль і два вимикаються, є три процеси на комп'ютері один(процес нуль, один і два), тобто максимальне навантаження на найбільш сильно занавантажееий комп'ютер − тричі більше за нормальне навантаження. Тому, для схеми відновлення у мал. 2 комбінація комп'ютерів нуль і два, що ламаються, несприятливіша, ніж комбінація з комп'ютерів нуль і один. Наші результати також дійсні, коли є системи n зовнішнього живлення даних всередині кластера, наприклад один телекомунікаційний центр постачає дані для кожного комп'ютера у кластері. Якщо комп'ютер віключається, центр повинен направити свої дані на деякий інший комп'ютер в кластері, тобто повинен бути "списком відновлень", що асоціюється з кожним обиінним центром. Несправна команда може альтернативно бути владнана списком відновлення що складає список на рівні протоколу комунікації, наприклад IP [8]. Багато кластерних виконувачів пропонують не лише щоб користувач визначив дані схеми відновлення тут, але і динамічне навантаження, що балансує схеми у разі вимкнення комп’ютера.
Мал. 2 Виконання додатка в кластері з чотирьох комп’ютерів
Мал. 3 Розподілення навантаження в телекомунікаційній системі, Коли один з комп’ютерів вимкнувся
Непередбачувана поведінка в найгіршому випадку і відносно числа часу затримки переходу такої динамічної схеми є, проте, неприваблива у багатьох додатках в режимі реального часу. Також зовнішні системи не можуть користуватися динамічним навантаженням, що балансує схеми, коли їм треба вибрати новий вузол, коли первинне місце призначення для їх продукції не відповідає. Тому результати, представлені тут, дуже релевантні для систем, де кожен вузол має його власну мережеву адресу. Крупно розділені кластери повинні знати, де робота піде, якщо поточні комп'ютери вимкнуться. Причина, ми переконані, що усі необхідні дані копіюються в комп'ютер, на якому робота починається заново після вимкнення і для великих кластерів ми не можемо копіювати усі дані в кожен вузол вкластера. Це означає, що ми повинні користуватися статичними схемами крупно розділених кластерів. Знайти хороші схеми відновлення − фундаментальна задача в розподілених і кластерних системах. Ми припускаємо, що робота, що виконується кожним з n комп'ютерів, має бути переміщена, як одна атомна одиниця. Наприклад − системи, де уся робота, що виконується комп'ютером робиться від однієї зовнішньої системи або коли усю роботу виконує один процес чи система, де зовнішньою комунікацією управляє IP протокол [8] (у цьому випадку увесь зовнішній рух за однією мережевою адресою спрямовується за мережевою адресою як одна атомна одиниця). Випадок, коли ряд процесів на кожному комп'ютері, і його процесах може бути перерозподілений один незалежно від одного обговорюється в Додатку. Результати грунтуються на загальних результатах, які підсумовуються в Секції 3. У Секції 4 ми подали заздалегідь використані схеми відновлення, ощадну і схему відновлення Голомбо. Модульні-m схеми визначаються в Секції 5 і порівняння схеми Голомбо в Секції 6. Секція 7 містить укладення використання модульної лінійки.
Попередня робота Ми починаємо з представлення деяких систем позначень. Розглядаємо кластер з n комп'ютерами. Нехай L(n > x) означає навантаження на найбільш сильно занавантажееий комп'ютер коли комп'ютери c0,., cx −1 вимикаються і користуючись схемою відновлення RS. Нехай max L (n, x, RS) = L (n, x, { c0,., cx −1}, RS) для усього вектора { c0,., cx −1}, тобто для усіх комбінації x комп'ютерів, що вимикаються. Тому, L (n, x, RS) визначає робочу поведінку. Схема відновлення повинна поширювати навантаження як можна порівну для будь-якого числа вимкнених комп'ютерів x. Маленькі значення x ( багатообіцяючі) звичай інші чим великі значення x. Нехай V (L (n, RS)) представляє {L(n, 1, RS),.,L(n, n −1, RS)}. Відмітьте, що VL – вектор довжиною n −1 відколи ми ігноруємо випадок, коли усі n комп'ютери вимкнулися. Ми говоримо, що V (L (n, RS)) послідовно меньший, ніж V(L( n, RS')), якщо входи є ідентичні аж до порядкового y, і для цього показника міри значення V (L (n, RS)) менше, ніж V (L (n, RS')). Отже, для деяких y < n, які ми маємо 1. L (n, y, RS)< L (n, y, RS') і 2. L (n, z, RS) = L (n, z, RS') для усього z < y. Якщо y = 1, цього досить для L (n, y, RS)< L (n, y, RS'). Якщо V (L (n, y, RS)) послідовно меньше, ніж V(L(n, y, RS')), ми розглядаємо RS як кращу схему відновлення, ніж RS', наприклад для V = V (L (n, y, RS)) ={2,2,3,3,3,4,4} і V' = V (L (n, y, RS')) ={2,3,3,3,3,3,3} V послідовно меньше, ніж V'. Поведінка коли декілька комп'ютерів вимикаються вище розташована по пріоритетах порівняно з тим, коли багато комп'ютерів вимикаються. Зворотне твердження до " V (L (n, y, RS)) послідовно меньше, ніж V(L(n, y, RS')) " є“ V (L (n, y, RS')) послідовно більше, або дорівнює V(L (n, y, RS)) ". Потім також V (L (n, y, RS)) і V(L(n, y, RS')) ідентичні, або V(L(n, y, RS) ) послідовно менші V (L (n, y, RS')). Нехай VL = min V (L (n, RS)), де мінімум прийнятий усіма схемами відновлення RS. У [6] ми визначили нижчу межа B на VL, тобто B ≤ VL (B − вектор довжина n −1) шлях, за допомогою якого i−ітий вхід в B є: B (i) = max (BV (i), n ⁄(n – i)). BV − межа вектора довжиною l = 2+3+4+.+ k, визначили, як: {2,2,3,3,3,4,4,4,4,5,5,5,5,5,., k, k,., k }, де n−те вхід в послідовність рівний Ми подали також схеми відновлення RS для n ≤ 11 такі, що V (L (n, RS)) = B. Вони − представлені як оптимальні схеми відновлення, коли більшость log2n комп'ютерів вимикається. У [6] ми подали нові схеми відновлення − поліпшили схеми відновлення, названі також ощадними схемами відновлення, які оптимальні для більшого ряду важливих випадків. Вони послідовно менші, ніж схеми описані в [6]. Ми також показуємо, що задача виявлення оптимальних схем відновлення відповідає які суми послідовностей унікальні. У [5] інший клас схем відновлення були представлені: схеми Голомбо. Вони послідовно меньші, ніж ощадливі схеми. Перевага ощадливого алгоритму, порівнянно з схемами Голомбо, є, що ми можемо легко вичислити послідовність з чіткими частковими сумами також для великого n, де немає послідовностей Голомбо, також названих лінійкою. Недолік з схемами Голомбо є, що послідовності відомі тільки довжинами аж до 41912 (з 211 позначками), які означають, що для кластера з 41912 комп'ютерами робота поширюватиметься порівну, якщо 212 комп'ютерів зламані. Тільки першші 373 лінійки (з 23 позначками) Голомбо, відомо, оптимальні [11,12,13].
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-22; просмотров: 295; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.26.231 (0.01 с.) |



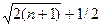 .
.


