
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Частина 1: Межі продуктивності в Паралельному ОбчисленніСодержание книги
Поиск на нашем сайте
1. Розглядаємо дві паралельних архітектури: Симетричний Мультипроцесор (SMP) з динамічним розподілом і розподілену систему (чи групу) із статичним розподілом. Накільки коротшим може час завершення паралельної програми бути на SMP, порівняно з розподіленою системою, за умови, що ми користуємося оптимальними графіками? 2. Розглядаємо мультипроцесор з ідентичними процесорами і паралельним програмним укладенням з незалежних процесів, і оптимального графіку з пріоритетними перериваннями. Якщо число пріоритетних переривань підвищене, наскільки великою може бути вигода при завершенні паралельної програми? Частина, 2:, Завантажують балансування в Паралельному Обчисленні 3. Розглядаємо групу з рядом комп'ютерів. Розглядаємо сценарій аварійної відмови у випадку, коли самі несприятливі комбінації комп'ютерів ламаються. Як може завантаження бути порівну і ефективно перерозподілене серед поточних комп'ютерів (користування статичним повторним поширенням)? Дослідницька Методологія Відколи ми зацікавлені в найгірших сценаріях випадку екстремального значення в нескінченних множинах, ми не можемо користуйтеся емпіричним методом, щоб знайти відповіді на дослідницькі питання теоретичних технік, що призводять до використання явних найгірших програм. Коректність заснована на математичних доказах (Статтяи 1 і 2). До того ж, ряд випробувань на мультипроцесорі і поширення середовища SUN/Solaris були зроблені, щоб перевірити правильність і ілюструвати деякі з результатів в Статті1. У Статті 2 ми скористалися теоретичним номером, формулою, заснованою на дереві Stern-Brocot. Статті 3 і 4 також засновані на теорії чисел. У Статті 3 ми показуємо схеми, які засновані на так званих правилах Голомбо. Правила Голомбо раніше були використані в різних випадках, наприклад в радіо-астрономії (розміщення антен), Ретнгено-кристалографії, кодуванні даних, географічному розміщенні і хеш-таблицях. У Статті 4 ми відобразимо більш докладно дані із Статті 3, додаючи новий вид правил "Правила Модуло", даючи результат, тобто дійсний у більших випадках, ніж у Статті 3. У Статті 5 ми знову розширюємо правила Голомбо, конструюємо нову схему відновлення, яка дає кращу продуктивність (швидкодію). У Статті 6 ми даємо вичерпну інформацію про випадки обчислення кращих можливих схем відновлення будь-якого числа пошкоджених комп'ютерів branch-and-bound алгоритмом.
Дослідницьке Сприяння Основні заключення в цій дисертації є: Частина 1: оптимальні межі: • оптимальну межу на мінімальному часі завершення для усіх паралельних програм з n обробками і мірою деталізації синхронізації z, що виконується у багатопроцесорній системі із статичним розподілом з k процесорами і затримкою комунікації t, порівнюємо з системою динамічного розміщення з q процесорами (подивіться Статтю1 і Секцію 4.1.1): H (n, k, q, t, z) = minAH (A, n, k, q, t, z). Тут А означає розміщення процесів до процесорів, де (aj) – процеси, що розміщені на j-ному комп'ютері Отже, розміщення представлене послідовністю розміщення(a 1, …, ak), де. До того ж H (A, n, k, q, t, z) = g (A, n, k, q)+ zr (A, n, k, t) Де g (A, n, k, q)= Сума прийнята усі послідовності, що зменшуються ненегативні цілі числа таке, I = { i 1, …, ik } що. ij
• оптимальна межа на мінімальному часі завершення паралельної програми виконується у багатопроцесорній системі з порівнянням процесорів м, графіками з двома різними номерами пріоритетних переривань i і j, де (подивіться Статтю2 і Секцію 4.1.2):
Тут зображення знаками приходить від наступного визначення:
Визначення:, де максимум прийнято усю безліч цілих чисел і таким чином, m 1, …, mc n 1, …, nc що , хоча і m 1 + … + mc = m n 1 + … + nc = n mk > 0 nk ≥ 0 (Lennerstad і Lundberg, [40]). Частина, ДРУГА: алгоритми: • Схема відновлення Голомбо (подивіться Статтю3 Секція 4.2.1) • Схема відновлення Модуло (подивіться Статтю4 Секція 4.2.2) • Трапеціальна схема відновлення(подивіться Статтю 5 Секція 4.2.4) • Оптимальна Схема відновлення (подивіться Статтю 6 Секція 4.2.3) Багатопроцесорне Планування (Частина I) У цій секції ми представляємо класифікацію планування проблем і присутню роботу, пов'язану з межами і складностями для деяких з них. Дуже хороша таксономія завдання планування в розподілених системах обчислення представлена в Casavant і Kuhl в [8] (подивіться Мал. 2). Тут, статичні засоби недоступні, тобто, рішення для процесу зроблене перед тим, як воно виконуватиметься, при динамічних засобах он-лайн, тобто, коли невідомо, коли і де процес виконуватиметься впродовж його тривалості життя. У Статті1 і 2 ми розглядаємо глобальне оптимальне статичне планування, коли ми знаємо інформацію з паралельної програми заздалегідь.
2.1 Класифікація планування проблем Ми починаємо з визначення планування, що розвивається по схемі Graham, Lawler, Lenstra і Rinnooy Kan [28]: Розглядаємо машини м Mi (i = 1,..., m) яким треба обробити n роботи Jj (j = 1,..., n). Графік - розміщення одного або більше інтервалів часу на одній або більше машинах для кожної роботи. Графік виконується, якщо два інтервали часу розподілили для того ж робочого перекриття, і якщо, крім того, це відповідає ряду специфічних вимог з приводу машинного середовища і робочих характеристик. Графік оптимальний, якщо це мінімізує критерій оптимальності. До того ж, автори (Graham і інший. [28]) запропонували класифікацію планування проблеми, яка була широко використаниа в літературі, наприклад Lawler і інший. [38], Blazewicz і інший. [4], Pinedo [55]. Класифікація показує, скільки проблем в плануванні теорії може бути, якщо б ми подивилися на усі комбінації. Ця дисертація обмежена одним типом машин і в одному критерії, тобто мінімальному часі завершення. Класифікація планування проблеми представляється як трипільна класифікація, де представляє середовище процесора, робочі характеристики і критерій оптималності як зазначено нижче: Перше поле α = α1α2 складається з двох параметрів:α1 ∈{°, P, Q, R, O, F, J } де (означає порожній символ) представляє єдиний процесор; P: ідентичні процесори; Q: однорідні процесори, тобто процесори з цією швидкістю; R: unrelated процесори тобто процесори із залежними для роботи швидкостями; O: виділяємо процесори: відкрите з цехове встановлення послідовності, в якому кожну роботу доведеться обробити знову на кожному одному з м процесорів; немає ніяких обмежень відносно замовлення кожної роботи; F: виділяємо процесори: відкрите цехове встановлення послідовності, в якому кожну роботу доведеться обробити на кожному одному з процесори м із спеціальним замовленням, тобто спочатку на процесі один, потім на процесі два і так далі. Після завершення на одному процесорі, робота приєднується до черги в наступному процесорі; J: виділяємо процесори: встановлюємо послідовності роботи обчислювального центру, кожна робота має свій власний наказ слідувати; і: число процесорів (Pinedo, [55]) У Статті 1 ми описуємо сценарій ідентичних машин з різним числом процесорів, тобто множина Pk для паралельної архітектури з k ідентичними процесорами і статичний розподіл, і множина Pq - з q ідентичними процесорами і динамічним розподілом. Потім. В Статті2, тут ми також описуємо сценарій ідентичних машин з процесорами м. Друге поле описує робочі характеристики. Тут ми описуємо тільки щось з можливих значень β ∈{°, pmtn, prec, tree, res, rj, pj = 1}., де йде на увазі, що це немає ніяких обмежень на роботи; pmtn означає, що пріоритетні переривання дозволяються; prec є перевагою відношення між роботами, дерево - деревне представлення, що вкорінилося; ре вказане обмеження ресурсу; rj - дата вручення; pj = 1: кожна робота має одиничну обробку вимоги (відбувається, тільки якщо α ∈{°, P, Q }). У Статті 1 ми не маємо ніяких робочих характеристик, так для обох випадків (Pk і Pq) У Статті 2, ми відобразили сценарій з обмеженим числом пріоритетних переривань, тобто, останнє поле описує критерій оптимальності. Зазвичай вибраним найбільшим є час максимального завершення або робочий інтервал (C max), повний час (Σ Cj) завершення чи максимальне запізнення L max, де запізнення завдання - його час завершення крайній термін [Graham і інший., 28].\
У Статті1 і 2 ми зацікавлені в зменшенні робочого інтервалу, тобто для мінімізації часу максимального завершення, тобо γ = C max. Користуючись цим відображенням, ми можемо представити проблему зменшення максимального завершення часу на ідентичних паралельних машинах, що дозволяють пріоритетне переривання, як P pmtn C max. Межі і Складність на Багатопроцесорному Плануванні Проблема планування паралельної програми по машинах м була показана, в класі складності НП (Garey і інший., [21]). Багато плануючих проблем просто щоб вирішити, коли ми дозволяємо пріоритетним перериванням, наприклад проблема зменшення часу (Cmax) максимального завершення без пріоритетних переривань на двох ідентичних процесорах (P 2 // C max) в класі складності НП при проблемі для пріоритетного паралельного планування більш ніж для 2 процесорів P pmtn C max вирішуваних в часі (McNaughton, [50]) O(n). Проте, там є все ще практичне питання дозволу або не дозволу пріоритетним перериванням. У 1966, Graham [26], користуючись правилом Списку планування, довів, що: C max(LS) C max ⁄ * ≤2–1⁄ m, де м є числом процесорів і означає час максимального завершення для оптимального графіку. Ідея списку, планування, необхідна для того, щоб скласти замовлений список процесів, призначаючи їм деякі пріоритети. Наступна робота від списку призначена першій доступній машині. Один з найбільш часто користувних алгоритмів для вирішення P// C max проблеми – «Найдовший час опрацювання» НЧО який є свого роду списком планування. Тут, роботи упорядковуються в зменшенні обробки замовлення часу і коли машина доступна, найбільша робота готова почати оброблятися. Складність цього алгоритму є O (n log n) і верхня межа встановлена Грехемом ([27]): Леннерштадт і Люндберг [39] встановлюють оптимальну верхню межу на вигоді користуючись двома різними паралельними архітектурами без міграцій процесів, де число процесорів в обох системах рівні. У [41] результат є розширено, для сценарію з різним числом процесорів. У Статті 1 - розширенні такі списки, як вартість комунікації і синхронізації між процесорами (Стаття 1 Секція 4.1.1). Проблема зменшення робочого інтервалу з пріоритетними перериваннями,
У Другій статі, ми розширюємо результати Braun і Schmidt-а [5], порівнюючи пріоритетний графік з j пріоритетними перериваннями до графіку з i < j пріоритетними перериваннями, де (Стаття 2 Секція 4.1.2).
|
||||
|
Последнее изменение этой страницы: 2016-06-22; просмотров: 301; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.242.20 (0.008 с.) |


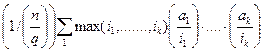 і
і 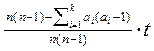
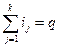



 , Проте, в алгоритмі НЧО, нехтують значенняю синхронізації і перерозподілу навантаження. Для досягення кращого виконання представляється інший опосередкований алгоритм, під назвою «Мультифіт» з робочим інтервалом
, Проте, в алгоритмі НЧО, нехтують значенняю синхронізації і перерозподілу навантаження. Для досягення кращого виконання представляється інший опосередкований алгоритм, під назвою «Мультифіт» з робочим інтервалом  , на якому. Цей алгоритм заснований на binpacking техніці, де роботи(завдання) розміщені не в порядку зростання, і кожна робота є розміщено в першому процесорі, до якого вона найкраще підходить. Ця межа була крім того вдосконалена Фрізеном і Лангстоном [20] а потім Юе [62] її допрацювів. Хохбаум і Шмойс [29] розробили багаточленну упосередковану схему, що заснована на підході «мультифіт», з обчислювальною складністю
, на якому. Цей алгоритм заснований на binpacking техніці, де роботи(завдання) розміщені не в порядку зростання, і кожна робота є розміщено в першому процесорі, до якого вона найкраще підходить. Ця межа була крім того вдосконалена Фрізеном і Лангстоном [20] а потім Юе [62] її допрацювів. Хохбаум і Шмойс [29] розробили багаточленну упосередковану схему, що заснована на підході «мультифіт», з обчислювальною складністю 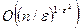 для n процесів.
для n процесів. може бути вирішена дуже ефективно із складністю часу O (n). Робочий інтервал любого спланованого переривання як мінімум
може бути вирішена дуже ефективно із складністю часу O (n). Робочий інтервал любого спланованого переривання як мінімум  Проте за встановленими правилами Макнатона не більше ніж m – 1 пріоритетні переривання потрібні у безмежному випадку. Для планування з обмеженнями переваги, тобто, P
Проте за встановленими правилами Макнатона не більше ніж m – 1 пріоритетні переривання потрібні у безмежному випадку. Для планування з обмеженнями переваги, тобто, P  Грехам [26]
Грехам [26]  . правила Грехама що були впровадженні в 1996 році досі використовуються. Якщо роботи мають модульну довжину проблема НП-Комплексності. Проте, якщо число процесорів обмежене 2ма, тоді
. правила Грехама що були впровадженні в 1996 році досі використовуються. Якщо роботи мають модульну довжину проблема НП-Комплексності. Проте, якщо число процесорів обмежене 2ма, тоді  вирішуваний вчасно O (n 2). Coffman і Garey [11] доводять, що найменший досяжний робочий інтервал з непріоритетним графіком складає не більше ніж 4/3 найменший досяжного робочого інтервалу, коли пріоритетні переривання дозволяється. У 1972, Лью [43] здогадується, що для будь-якої безлічі завдань і обмежень переваги серед них, працюючи на двох процесорах, найменший робочий інтервал, досяжний непріоритетним графіком - не більше ніж ¾ найменшого робочого інтервалу, досяжного пріоритетним графіком. Здогадка була доведена в 1993 Coffman і Garey [11]. Тут автори узагальнюють результати до номерів 4/3, 3/2, 8/5,... тобто до номерів 2 k ⁄(k + 1) для деяких k ≥ 2. номер k залежить від відносного числа доступних пріоритетних переривань. Braun і Schmidt -ом[5] в 2003 доведена формула C max, яка порівнює пріоритетний графік з i пріоритетними перериваннями C max до графіку з безмежним числом пріоритетних переривань в найгіршому випадку. Вони узагальнили межу 4/3 до формули C max
вирішуваний вчасно O (n 2). Coffman і Garey [11] доводять, що найменший досяжний робочий інтервал з непріоритетним графіком складає не більше ніж 4/3 найменший досяжного робочого інтервалу, коли пріоритетні переривання дозволяється. У 1972, Лью [43] здогадується, що для будь-якої безлічі завдань і обмежень переваги серед них, працюючи на двох процесорах, найменший робочий інтервал, досяжний непріоритетним графіком - не більше ніж ¾ найменшого робочого інтервалу, досяжного пріоритетним графіком. Здогадка була доведена в 1993 Coffman і Garey [11]. Тут автори узагальнюють результати до номерів 4/3, 3/2, 8/5,... тобто до номерів 2 k ⁄(k + 1) для деяких k ≥ 2. номер k залежить від відносного числа доступних пріоритетних переривань. Braun і Schmidt -ом[5] в 2003 доведена формула C max, яка порівнює пріоритетний графік з i пріоритетними перериваннями C max до графіку з безмежним числом пріоритетних переривань в найгіршому випадку. Вони узагальнили межу 4/3 до формули C max .
.


