Визначення і основні результати

Позначення

У статті ми користуємося наступними кількостями і позначеннями: n: число процесів в паралельному програмному; k: число комп'ютерів в розподіленій системі, тобто система без перерозподілу під час виконання Мал. процесів (1a); q: число процесорів в SMP, тобто система з перерозподілом під час виконання з процесів (Мал. 1b); t: вартість комунікації між комп'ютерами в розподілений системі (Мал. 2b); z: міра деталізації паралельної програми; P (a 1, …, ak): розміщення

послідовності, числа процесів розподілено для комп'ютера x як ax;

Рис 1а) Розподілена мультипроцесорна система з «к» комп’ютерами що містять по одному процесору 1б) СМП- мультипроцесорна система що складається з одного комп’ютера що містить «ку» процесорів.

Рис 2. а) Оптимальна динаміка і б) статика і розподіл програм Р що виконується на 2х процесорах.

 

(y 1, …, yk (k – 1)⁄ 2) послідовність синхронізації, де yi - число синхронізацій

між парами процесів; Td (P, q): час завершення для програми Р з оптимальним динамічним розподілом (Мал. 2a); Ts (P, k, t): час завершення для програми Р з оптимальним статичним розподілом (Мал. 2b);: Ts (P, A, k, t) Ts (P, A): час завершення для програми Р з певним статичним розподілом (Мал. 2b); g (A, n, k, q) функція, що зв'язує час завершення частини виконання програми; r (A, n, k, t)

: функція, що зв'язує час завершення частини синхронізації програми; H (n, k, q, t, z): оптимальна функція, що зв'язує повний час завершення програми, тобто основний результат цієї статті.

 

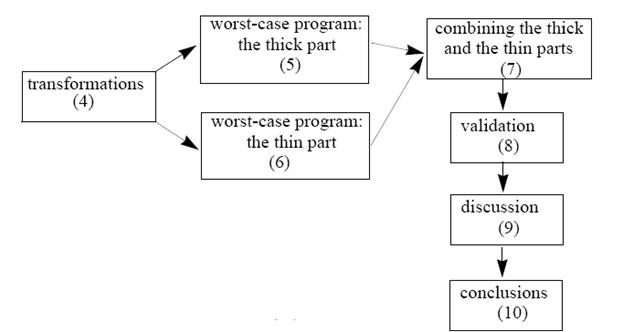
Визначення

Ця секція описує визначення і показує відмінності між динамічним і статичним розподілом.

Ми розглядаємо паралельну програму з n процесами. Мал. 2 Показує паралельну обробку Р що складається з трьох процесів (Р₁ Р₂ Р₃), що виконуються на двох процесорах. Тривалість виконання кожного процесу дорівнює 2. Послідовна обробка представлена процедурою обробки. Отже, Робота(x) означає послідовну обробку для одиниць x часу. Для безперебійної частини виконання процесу, який не містить ніякої синхронізації ми іноді використовуємо термін «Сегмент». Тому, сегмент довжина x представляється Роботою(x).

Процеси синхронізують з двома примітивами: Активізувати і Очікувати. Процес не блокується, коли іде виконання опції «Активізувати»; коли виконується «Очікування», процес стає блокованим до передачі сигналу «Активізувати» на виконання. Якщо передача «Активізувати» була виконанана перед тим, як процес досягне «Очікування», тоді процес виконання «Очікування» не блокується. У Мал. 2 ми бачимо цей процес Р1 не може запуститись до виконання перед тим, як Р2 активізовано (Активізують(Подію_1) в Р2

Потім Р2 очікувє сигнал від Р1 щоб запуститися. Це залежність представляється в «Очікуванні(Подія_3)» в процесі і «Активізацією(Події_3)» в процесі Р1, іноді називають сигналом синхронізації. Отже синхронізаційний сигнал - команда в процесі, який активізує інший процес. Паралельна програма має чіткий стартовий покажчик в термінахдеякої частини коду в одному процесі, яка повинна виконуватися перед будь-яким іншим процесом що виконується. Є також чіткий кінцевий покажчик в термінах частини коду в тому ж процесі, яка повинна виконуватися врешті-решт коли інші процеси завершили своє виконання. У Мал. 2, процес Р2 - процес, що містить частину коду, яка виконується перед тим, як будь-який інший код буде виконватись, і частина коду, яка виконується, врешті-решт коли інший код був виконаний. Це дуже загальна структура в реальних паралельних програмах, де основний процес відповідальний за старт виконання і за впевненість в тому що всі процеси було виконано до того як програма завершила свою роботу.

Динамічний розподіл означає, що процес, можливо, виконується різними процесорами

впродовж періодів різного часу. Процеси, можливо, переносяться між усіма процесорами без обмежень.

Оптимальний динамічний розподіл - розміщення процесів між процесорпми, для яких час завершення паралельної програми коротший, ніж або рівний часу завершення, користуючись будь-яким іншим динамічним розподілом. Час завершення для оптимального динамічного розподілу для програми з (SMP) мультипроцесором з q процесорами означає Td (P, q). Ця кількість включає тільки виконання відколи в динаміці вартість сигналів синхронізації нульова.

У статичному розподілі процес може виконувати тільки той процесор, на якому дія була створена. У цьому докладі, що є протилежним до попередніх випадків, ми не нехтуємо часом синхронізації в статичному випадку. Ми виражаємо вартість комунікації для будь-якого синхронізаційного сигнала t. Для статичного розподілу, на час завершення впливає місце дії планування. Локальним плануванням ми виражаємо, що шлях обробки, для якого розподілено такий же процесор планується в межах власного процесора. Для певного статичного розподілу оптимальне локальне планування - локальний плануючий алгоритм розподілу ресурсів, який приводить найкоротший час завершення. Оптимальний статичний розподіл - розміщення, для якого завершення час, що користується оптимальним локальним плануванням, коротший, або дорівнює до часу завершення будь-якого іншого статичного розподілу, користуючись оптимальним локальним плануванням. Ми визначаємо час завершення з оптимальним статичним розподілом для програми Р, користуючись розподіленою системою з k комп'ютерами, і вартістю синхронізації t, Ts (P, k, t). Ця кількість включає обидва виконання і часи синхронізації. Тривалістю виконання часто буде названа час самої роботи.

Права сторона рис. 2 графічне представлення і його оптимальна динаміка (Мал. 2a; мультипроцесор з одним комп'ютерним що містить два процесори) і статичні розподіли (Мал. 2b; мультипроцесор з двома комп'ютерами, що містять один процесор кожен).

У динамічному розподілі (Мал. 2a), процеси, можуть, бути розприділено між усіма процесорами

без обмежень, наприклад процес Р3 виконується на двох процесорах. Тут вартість комунікації дорівнює нулю, тому що процеси виконуються в тому ж комп'ютері. Робочий час кожного процесу в прикладі, показаному в Наряді 2, дорівнює 2. Додаючи робочий час усіх процесів не враховуючи програмну синхронізацію, ми отримуємо повний робочий час цієї програми. Число сигналів синхронізації в програмі Р

ділиться на повний робочий час, бо програма викликається мірою деталізації програми і позначається z. У прикладі рис. 2, міра деталізації z дорівнює 5/6.

3.3 Основні результати і план статті

Дані параметри n, k, q, t і z, ми характеризуватимемо як набір найгірше працюючих програм що матимуть назву «завершених». Ми робимо це починаючи з довільної програми і виконуючи послідовні перетворення. У кожному перетворенні програма стає "більш погано працюючою" в сенсі, що діапазон TS (P, k, t)⁄ Td (P, q) не зменшується.

Кінцевий результат - безліч завершених програм. Ці програми цілком мають таке. ж TS (P, k, t)⁄ Td (P, q) Відколи ми починаємося з довільної програми, ми враховуємо що програма є "більш погано працюючою», відколи вони мають максимальний TS (P, k, t)⁄ Td (P, q).

План статті представляється в Мал. 3. Ми починаємося з (Секції 4) з деяких перетворень

з однієї програми в копіях м цієї програми це дозволяє нам розбивати програму на дві частини. Перша частина складається з усього виконання, і описується в Секції 5. Друга частина, складається тількуи з синхронізації і, описується в Секції 6. У Секція 7 ми комбінуємо результати від цих частин в цілій програмі і тут є присутня формула для H (A, n, k, q, t, z) = g (A, n, k, q)+ zr (A, n, k, t). Перша умова сума, що приходить з Секції 5, і другий з Секції 6. Формула H (n, k, q, t, z) = minAH (A, n, k, q, t, z)

зв'язує час завершення для будь-якої програми з n процесами, міра деталізації z і вартістю комунікації t наступною нерівністю. Ts (P, k, t)≤ H (n, k, q, t, z) Td (P, q):

.

Тут. Ts (P, k, t) = min ATs (P, k, t, A) у функції H (n, k, q, t, z)є оптимальною в розумінні, що щонайменше для деякої програми:: P Ts (P, k, t) = H (n, k, q, t, z) Td (P, q).

 

Тому, для усіх програм::.

У Секції 7 ми подємо алгоритм «Гілок і меж» для ефективного обчислення H (n, k, q, t, z) H (A, n, k, q, t, z).

Рис. 3 – План статті