Схеми Голомбо проти схеми модуля

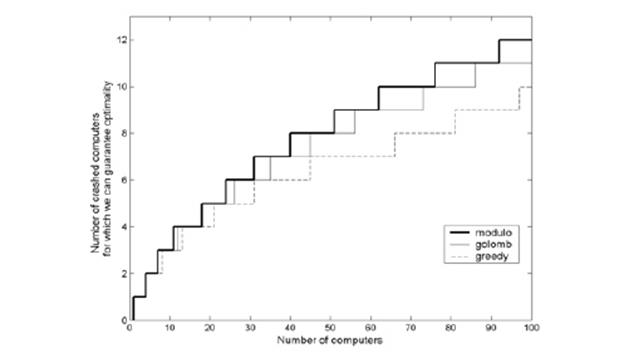
Послідовність модуля може бути визначена як окремий випадок лінійки Голомбо з l позначками d 1 d 2 … dl, з властивістю, що усі різниці (dj − di) mod n чіткі, для i < j, і що усі (dj − di) mod n не нульові. Відколи є відмінності ми обов'язково маємо n ≥ + 1. Послідовність модуля з точним чіткі відмінності так звана лінійка досконалого модуля. Повні перебори вказують, що немає лінійки досконалого модуля, коли l > 5.

У Таблиці 2 модульні послідовності і послідовності Голомбо порівняні. Послідовності рівні для маленьких кластерів. Ми можемо гарантувати оптимальний навантаження, що балансує для більшого номера комп'ютерів з пошкодженнями, якщо ми користуємося послідовностями модуля, ніж послідовності Голомбо, які означає, що схеми Голомбо послідовно більші, ніж схеми модуля, і що залишається близько до вектору BV. Наприклад, в цьому випадку 76

 

Довжина послідовності	Модульна послідовність	m	Оптимальна лінійка Голомбо	n
	1,3		1,3
	1,4,6		1,4,6
	1,6,3,10		1,4,9,11
	1,3,7,17,12		1,4,10,12,17
	1,3,23,7,17,12		1,4,10,18,23,25
	1,5,7,18,27,30,15		1,4,9,15,22,32,34
	1,4,30,15,38,17,22,10		1,5,12,25,27,35,41,44
	1,4,48,33,9,50,25,39,19		1,6,10,23,26,34,41,53,55
	1,5,49,58,15,18,39,41,47,12		1,4,13,28,33,47,54,64,70,72
	1,5,43,34,55,65,71,14,41,73,58		2,6,24,29,40,43,55,68,75,76,85
	1,6,78,47,20,24,45,74,57,17,8,87		2,5,25,37,43,59,70,85,89,98,99,106

Таб. 1 Порівняння модульної схеми та схеми Голомбо

m = к−ть комп’терів в кластері при яких можна гарантувати опримальність використовуючи модульну схему

n = к−ть комп’терів в кластері при яких можна гарантувати опримальність використовуючи схему Голомбо;

 

Висновки

У багатьох кластерних і розподілених системах, проектувальник повинен забезпечити схему відновлення. Такі схеми визначають, як робоче навантаження треба перерозподілити, коли один або більше комп'ютерів вимикається. Мета − тримати навантаження, для якомога рівномірного поширення, навіть, коли самі несприятливі комбінації комп'ютерів вимикаюється, тобто ми хочемо оптимізувати поведінку найгіршого випадку.

Ми розглядаємо n ідентичні комп'ютери, які за нормальних умов виконують один процес. Усі процеси виконують ту ж кількість роботи. Схеми відновлення, що гарантують оптимальне поширення навантаження в найгіршому випадку, коли x комп'ютерів вимкнулися є так звано оптимальні схеми відновлення для значення n і x. Вкладення в цій статті, показують, що задача виявлення оптимальних схем відновлення системи з n комп'ютерами відповідає математичній задачі виявлення щонайдовшої послідовності додатніх цілих чисел таких, що сума иенша, ніж n і суми

Кинник алгоритму, який знаходить щонайдовшу послідовність з цими властивостями, не відомий.

Ми заздалегідь отримали схеми відновлення, які оптимальні, коли більша кількість з комп'ютерів вимикаються, але вони не покривають навантаження, що балансує, коли із запахом відбувається [6].

З послідовностями модуля ми мінімізуємо максимальний навантаження також у випадку «обгортки по колу». Послідовності модуля дають оптимальнішу поведінку більшого ряду пошкодженого комп'ютери, ніж Голомбо і ощадливі послідовності. Наприклад, в цьому випадку 92−107 комп'ютери в кластері, послідовності модульного-м гарантують оптимальну поведінку в цьому випадку

Мал 4 Представлення різниці між системою OGRs та ощадливою версією систем відновлення

12 вимкнень, поки лінійка Голомбо тільки гарантує оптимальність для 11 вимкнень, і ощадлива схема для 10 вимкнень. Перевага з ощадливим алгоритмом, порівнянним з іншими схемами, є, що ми можемо легко вичислити послідовність з чіткими частковими сумами також для великого n, де немає послідовності Голомбо а послідовності модуля відомі. Лінійка Голомбо відома довжинами до 41912 (з 211 маркою) [11,12,13]. З них перший 373 (з 23 позначками), відомо, є оптимальний, поки лінійка модуля відомі тільки 13 позначками. Послідовності модуля є відома тільки до 92 комп'ютерів в кластері. Наші схеми відновлення можуть бути негайно використані в комерційних кластерних системах, наприклад визначаючи список в Сонячному Кластері, користуючись scconf командою. Результати можуть також будьте використані, коли ряд зовнішніх систем, наприклад telecommunication центри, що переключають відправте дані різним вузлам в розподіленій системі (або кластері, де вузли мають individual мережеві адреси). У такому разі, списки відновлень також здійснюються як альтернативні місця призначення в зовнішніх системах або в протоколі комунікації рівень, наприклад переворот [IP 8].

Список літератури

1. Golomb, S. W., and Taylor, H., Cyclic Projective Planes, Perfect Circular Rulers,

and Good Spanning Rulers, Sequences And Their Applications – SETA’01, Proceedings

of Seta01, Bergen, Norway, May 2001, pp. 166−180

2. Hewlett−Packard Company, TruCluster Server − Cluster Highly Available Applications,

Hewlett−Packard Company, September 2002

3. Hewlett−Packard, Managing MC / ServiceGuard, Hewlett−Packard, March 2002

4. IBM, HACMP, Concepts and Facilities Guide, IBM, July 2002

5. Klonowska, K., Lundberg, L. and Lennerstad, H., Using Golomb Rulers for Optimal

Recovery Schemes in Fault Tolerant Distributed Computing, in Proceedings of the

17th International Parallel & Distributed Processing Symposium IPDPS 2003,

Nice, France, April 2003, pp. 213

6. Lundberg, L., and Svahnberg, C., Optimal Recovery Schemes for High−Availability

Cluster and Distributed Computing, Journal of Parallel and Distributed Computing

61(11), 2001, pp. 1680−1691

7. Microsoft Corporation, Server Clusters: Architecture Overview for Windows Server

2003, Microsoft Corporation, March 2003

8. G.F. Pfister, In Search of Clusters, Prentice−Hall, 1998

9. Sun Microsystems, Sun Cluster 3.0 Data Services Installation and Configuration

Guide, Sun Microsystems, 2000

10. TruCluster, Systems Administration Guide, Digital Equipment Corporation, http://

www.unix.digital.com/faqs/publications/cluster_doc

11. http://www.cuug.ab.ca:8001/~millerl/g3−records.html

12. http://www.distributed.net/ogr/index.html

13. http://www.research.ibm.com/people/s/shearer/grtab.html