
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Додаток: Неатомні НевантаженняСодержание книги
Поиск на нашем сайте
Досі, ми розглянули випадок, коли всяка робота по вузлу, що виконується комп'ютером має бути переміщена як одна атомна одиниця. Очевидно, може бути більш ніж одинпроцес на кожен комп'ютер і ці процеси можуть в деяких випадках бути перерозподіленим самостійно один з одного, і у такому разі є один список відновлень для кожного процесу. У цьому застосуванні ми розглядаємо випадок, де є p процеси на кожному комп'ютері. Ми переймаємо на себе що робоче навантаження − рівномірно розділіне між процесами. Попередні вивчення показують це, якщо є великий ряд процесів на кожному комп'ютері задача виявлення оптимальних схем відновлення стає менш важливою [6]. Причина − інтуїтивні рішення покращуються. Тому важливість отримання оптимальних схем відновлення найбільша, коли p прирівняне до n. У головній частині цієї статті, ми отримали результати для p = 1. Техніка використана для отримання тих результатів також корисна, коли ми вважаємо p > 1. Ми зараз визначаємо вектори межі типу p., вектори межі обговорювали в Секції 3 були типом один, тобто p = 1. Пов'язаний вектор типу p виходить в наступному шляху (перший вхід у вектор межі − вхід 1): 1. t = p; i = 1; j = 1; r = 1; v = 1 2. Якщо r = 1 потім t = t +1; r = j; v = v +1 інший r = r −1 3. Впустіть вхід i в Пов'язаний вектор type p мають значення t/p 4. i = i +1 5. Якщо v = p і r = 1 потім j = j +1; v = 0 6. Повертаємося до 2 вектору межі не має бажаної довжини.
Пов'язаний вектор типу двох виглядає подібно до цього (запис навантаження на кожному комп'ютері є нормалізовано до одного, коли усі комп'ютери працюють): {3/2, 4/2, 4/2, 5/2, 5/2, 6/2, 6/2, 6/2, 7/2, 7/2, 7/2, 8/2, 8/2, 8/2, 8/2, 9/2, 9/2, 9/2, 9/2, 10/2,… Пов'язаний вектор типу трьох виглядає подібно до цього: {4/3, 5/3, 6/3, 6/3, 7/3, 7/3, 8/3, 8/3, 9/3, 9/3, 9/3, 10/3, 10/3, 10/3, 11/3, 11/3, 11/3, 12/3… Пов'язаний вектор типу чотирьох виглядає подібно до цього: {5/4, 6/4, 7/4, 8/4, 8/4, 9/4, 9/4, 10/4, 10/4, 11/4, 11/4, 12/4, 12/4, 12/4, 13/4,… Ми зараз розширюємо визначення VL, щоб покрити не лише випадок, коли p = 1, але і випадок, коли p > 1. Тому, VL( 1 ≤ x < n) означає максимальне число процес ділиться з p (для того, щоб нормалізувати оригінальне навантаження до один) на найбільш сильно завантажений комп'ютер, користуючись оптимальною схемою відновлення і коли x комп'ютери вимикаються, не лише, коли p = 1, але і, коли p > 1. Засновано на p і n ми зараз визначаємо B в наступному шляху: B(i) = вхід максимуму (i в зв'яжіть вектор type p,). Коли p = 2 і n = 12, який ми отримуємо: B = {3/2, 4/2, 4/2, 5/2, 5/2, 6/2, 6/2, 6/2, 7/2, 12/2, 24/2}. Для p ≤ n, ми заздалегідь визначили схему відновлення − відновлення p-процес схема оптимальна, поки у більшості log2 n/p комп'ютери вимикаються [6]. Ми називаємо це p−процес, тому що ми розглядаємо випадок, де є p процеси на кожному комп'ютер, коли усі комп'ютери працюють. Ми зараз визначаємо схему відновлення p−процес модуля. Схема визначена коли p ≤ n (пам'ятають, що оптимальні схеми відновлення найбільш важливі, коли p є мале порівнянно з n. Ми покажемо, що ця схема відновлення оптимальна також, коли значно більш ніж log2 n/p комп'ютери вимикаються. Фактично, результати були присутніми у Секції 5 відповідають випадку, коли p = 1. Нехай M0 є схемою модуля для деяких n і M0(k) бути k входом в M0. Нехай потім Mi, j означає список відновлень модуля для процес j (0 ≤ j < p) на комп'ютерному i (0 ≤ i < n). Ми визначте Mi, j заснував на M0, тобто схема відновлення для нуля процесу в одному процесі схема відновлення визначила в Секції 5. Якщо M0(k) + j ⎣ n/p ⎦ < n, то Mi, j(M0(k) + i + j ⎣ n/p ⎦) специфікатор вирівнювання n, інше Мі, j(k) = (M0 (k) + i + j ⎣ n/p ⎦ + 1) mod n, де Mi, j(k) означає ціле число k в списках для процес j на комп'ютерному i. Таблиця нижче показує відновлення складає список, коли n = 11 і p = 2.
Теорема 2: Нехай MRSn означати схему відновлення p−процес модуля для n комп'ютерів з p процес на кожному комп'ютері, і нехай B є пов'язаним вектором типу p. У такому разі перший вхід в V (L (n, RSn)) дорівнює B(1), другий вхід в V(L(n, RSn)) рівний до B(2), третій вхід в V (L (n, RSn)) дорівнює B(3),. x-вий вхід в V(L(n, RSn)) дорівнює B(x), де x = max(i), таке, що R0(i)< (n/p). Доказ: доказ подібний до доведення Теореми 1. Як в цьому доказі, усі номери модуль n − будь-яке з додатніх цілих чисел 0, 1,..., n − 1. Нехай y (0 ≤ y < n) є найважче завантаженим комп'ютером, коли x комп'ютери вимкнулися де x = максимум(i), таке, що R0(i)< (n/p 0) списки нижче за показують можливі x* p послідовності комп'ютерів, яким треба вимкнутися для того, щоб додатковий процес закінчився на комп'ютерний y 1.1 1.2 … 1.х 2.1 2.2 … 2.х … р.1 р.2 … р.х
Починаючи з x = max(i), таке, що R0(i)< (n/p), ми бачимо, що не всеодно який комп'ютер не включається із списків x. Переглядаючи доведеньння Теореми 4 і Теореми 3, ми бачимо, що межа оптимальна, поки ніякий комп'ютер не входить в два такі списки. Теорема слідує. Стаття V Розширені Лінійки Голомбо як Нові Схеми Відновлення в Розподілених Залежних Обчисленнях
Kamilla Klonowska, Lars Lundberg, Hakan Lennerstad, Charlie Svahnberg Proceedings of the 19th IEEE International Parallel and Distributed Processing Symposium (IPDPS'05), Denver, Colorado, April 2005
Резюме Кластери і розподілені системи дозволяють толерантність до помилок і високу продуктивність через спільне використання навантаження. Коли усі комп'ютери працюють, ми захотіли б розподілити навантаження порівну серед комп'ютерів. Коли один або більше комп'ютерів ламаються навантаження на цих комп'ютерах має бути перерозподілене на інші комп'ютери в кластері. Перерозподіл визначає схема відновлення. Схема відновлення повинна тримати навантаження, як найоптимальніше, коли вимикаються навіть несприятливіші комбінації комп'ютерів, тобто ми хочемо оптимізувати поведінку найгіршого випадку. У цій статті ми знаходимо нові схеми відновлення, які засновані на так званій Лінійці Голомбо. Вона оптимальна для набагато більшого ряду випадків, ніж попередні результати. Ключові слова: високе представлення обчислення, кластери, толерантність до помилки, схема відновлення, Оптимальна Лінійка Голомбо. Вступ Балансування навантаження і придатність важливі в розподіленні в онлайн надійних системах. Крішна і Шін визначають толерантність до помилки як "здатність системи, негайно відповісти на несподівану помилку технічного забезпечення або програми" [13]. Багато толерантних до помилок обчислювальних систем, віддзеркалюють усі дії, наприклад кожна дія виконується на двох або більше подвійних системах таким чином, що, якщо одина робить, інша може прийняти її роботу. У [2] толерантності до помилки для розподіленого обчислення йдеться від широкої точки зору. Перевага користування кластерами, окрім толерантності до помилки, − навантаження, що розділяється між комп'ютерами [15]. Один може управляти цією задачею динамічно, де трансферні рішення не залежать від фактичного поточного стану системи. Задача з динамічною політикою є швидше непередбачувана. Інакше − слін користуватися статичною політикою, на якій загалом заснована інформація поведінки системи. Тут, трансферне рішення є незалежне від фактичного поточного стану системи. Це робить їх менш комплексними і більш передбачуваними, ніж динамічна політика [7]. Задача, що вивчається в цій статті: як рівномірно поширюють навантаження поточні комп'ютери, коли один або більше комп'ютерів в кластері вимкнені? Ми вважаємо це статичний перерозподіл роботи. Є головний комп'ютер, який виконує додаток за нормальних умов і вторинний комп'ютер, який приймає задачу, коли головний комп'ютер вимкнений. Можливо, також є третій комп'ютер, який приймає задачу, коли головний і вторинний комп'ютери − вимкнені, і так далі. Коли усі комп'ютери працюють, ми вживаємо захотів, щоб навантаження поширювалося порівну. Навантаження на деяких комп'ютерах буде, проте зростати, коли один або більше комп'ютерів вимикаються, але і за цих умов ми хотіли б розповсюдити навантаження як можна порівну на комп'ютерах, що залишилися. Поширення навантаження, коли комп'ютер вимкнений вирішене списком відновлення процесів, що виконуються на помилковому комп'ютері. Сукупність усіх списків відновлень названа схемою відновлення. Отже поширення навантаження повністю визначене схемою відновлення незважаючи на число комп'ютерів, які вимикаються. Найбільше кластерних виконувачів підтримують цей вид оновлення при помилках, наприклад nodelist в Sun Cluster [17], список пріорітетів MC/ServiceGuard (HP) [5], каскадна група в HACMP (IBM) [6], і лист представлення в Windows Server 2003 clusters (Microsoft, earlier called MSCS) [14]. Задача виявлення оптимальних (чи навіть кращих) схем відновлення вивчається в [8,9,10]. У цій статті ми обчислюємо схеми відновлення, гарантію завантажження балансу для більшого числа комп'ютерів в кластері. Робота розглядає найгірший сценарій випадку, який дуже релевантний в системах реального часу. Проблемне формулювання представляється в Секції 2. Наше попереднє дослідження на цій задачі описується в Секції3. У секціях 4 і 5 ми подали головні результати укладення представлені в Секції 6. Проблемне формулювання Ми припускаємо, що робота, що виконується кожним з n комп'ютерів, має бути переміщена, як одна атомна одиниця. Це дуже загальний сценарій, у тому числі випадки, коли: • робота, що виконується комп'ютером, робиться від однієї зовнішньої системи (в упакані в стек схеми відновлення здійснюються в зовнішніх системах, як другий, третій, четвертий,... альтернативні місця (альтернативні кластерні вузли) призначення у разі, якщо голвний, вторинний,... місця призначення вимкнені); • є одна мережева адреса для кожного комп'ютера і ми користуємося протоколом IP (або подібною технікою); • усю роботу, що виконується комп'ютером, робить один процес або група пов'язаних процесів, використовуючи загальні місцеві ресурси і отже має бути переміщений як одна одиниця. У [11,12] ми обговорюємо випадок, коли ряд незалежних процесів виконує кожен комп'ютер. Результати, представлені тут, можуть бути легко узагальнені до випадку з числом незалежних процесів на кожному комп'ютері при використанні тієї ж техніки, як в попередній статті [11,12]. Розглянемо кластер з n ідентичними вузлами, які за нормальних умов виконують один процес кожен. Усі процеси виконують ту ж кількість роботи. Ми бичимо схему відновлення для кластера, який визначає, де процес треба знову почати якщо його поточний вузол вимкнений. Схема відновлення повинна тримати навантаження балансним до кластера, коли навіть найнесприятливіша комбінація вузлів вимкнена. Схема відновлення має бути о вичислена для великого n у багатоплинному часі. Схема відновлення R складається із списків n відновлень – один список на процес. Нехай S є послідовність відстаней, тобто послідовність додатніх цілих чисел S =< s 1, s 2, …, sn – 1> де Коли один вузол в кластері ламається, навантаження на найбільш завантаженому вузлі в кластері (давайте називати це, вузол Z) міститиме дві роботи: власнe його і робота від вузла. Коли два вузли в кластері вимикаються, є дві можливості. Якщо обоє спочатку в послідовності рівні, навантаження на Z може містити три роботи: його власну, від вузла і від вузла. Ця ситуація представляється на Мал. 1a). Вузли і − пошкоджені вузли. Друга можливість − тоді, коли два перші номери в послідовності відмінні. У такому разі, Z може містити тільки дві роботи: його власну і від вузла або від вузла. Ця ситуація представляється на Мал. 1b). Тому, навантаження найгіршого випадку на Z менший, коли, ніж, коли s 1 ≠ s 2 Мал. 1b) також показує ситуації, коли три вузли в кластері вимикаються. Потім навантаження на Z може містити три роботи: його власну і від вузлів. Відмітьте, що в цьому випадку вузол − також пошкоджений вузол. Нійгірший випадок для трьох пошкоджених вузлів є тоді, коли перші з трьох номерів в послідовності рівні, тобто s 1= s 2= s 3. У такому разі, Z міститиме чотири роботи: його власну і від вузлів.
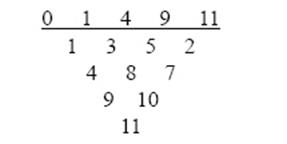
Мал. 1 Сценарій з трьма заламаними вузлами Попереднє дослідження У [12] автори ініціюють задачу виявлення схеми відновлення, яка може гарантувати оптимальне поширення навантаження найгіршого випадку, коли більшість k комп'ютерів вимикаються. Схеми повинні мати такий великий k як можливо. Автори представляють і доводять в Log алгоритм, це робить схема відновлення, яка гарантує оптимальність, де найбільше log2n комп'ютерів вимкнено. Оптимальний засіб, коли максимальне число процесів на тому ж комп'ютері після k вимкнень − MV(k), де функція MV(k) забезпечує нижню межу для будь-якої схеми статичного відновлення. Функція MV описується пізніше у Секції 4.1. Інший алгоритм, під назвою Ощадливий, представляється в [11]. Цей алгоритм генерує схеми відновлення, які дають оптимальність для більшого ряду випадків, ніж алгоритм Log (тобто. Ощадливий дає гарантії оптимальністі також, коли більш ніж log2n комп'ютерів вимкнені.). Ощадливий алгоритм заснований на математичній задачі виявлення послідовністі додатніх цілих чисел таких, що уся сума послідовностей унікальна і мінімальна. Це просто, для того щоб вичислити Ощадливий алгоритм навіть для великого n. Список відновлень для процесу нуль, виконуючись на комп'ютері нуль, складається з двох частин. Перша частина − послідовність від ощадливого алгоритму, і з другою частиною заповненою номерами, що залишилися. Інші списки із самого початку, включають єдиний сенс (як описано в Секції 2 в цій статті) модуля. Схема відновлення складається з усіх списків відновлень. Окремий випадок Ощадливого алгоритму − алгоритм під назвою Голомбо, описав [9]. Ім'я цього алгоритму походить від лінійки Голомбо, яка є послідовністю додатніх цілих чисел таких, що немає двох чітких пар, номери від множини мають ту ж різницю. Ці номери − названі позначками і відповідають позиціям на лінійному масштабі. Різниця між значеннями яких-небудь двох позначок названа відстанню. Найкоротша лінійка Голомбо для цього ряду позначок названа Оптимальною Лінійкою (OGRs) Голомбо[3]. Пошук Оптимальної Лінійки Голомбо стає важчим, оскільки число позначок зростає. Це відомо як NP−complete задача [16]. Задача виявлення OGRs для великого ряду позначок є ще невирішеною. Приклад представлення OGR з чотирма позначками показується в Мал. 2. Можливо виміряти відстані: 1; 2; 3; 4 як 1+3; 5; 7 як 5+2; 8 як 3+5; 9, як 1+3+5; 10 як 3+5+2 і 11 як 1+3+5+2, але ми не можемо виміряти відстань 6.
Мал. 2 представлення лінійки Голомбо для чотирьох позначок Лінійки Голомбо можуть також бути представлені як трикутник, де кожен номер представляє різницю між парою специфіки номерів. Мал. 3 показує приклад з чотирма позначками (такий же приклад, як в Мал. 2).
Мал. 3 Трикутне представлення лінійки Голомбо У лінійки Голомбо циклічні переходи проігноровані, тобто ситуації, коли підсумок числа "стрибків" для процесу більше, ніж число комп'ютерів в кластері. ("стрибок" − відстань між пошкодженим вузлом і вузлом, на якому процес треба бути знову почати). У тому числі циклічні переходи дають нове математичне формулювання з виявленням щонайдовшої послідовності додатніх цілих чисел таких, що сума і суми з усього модуля послідовностей (у тому числі послідовності довжини один) n унікальні (для цьго n). Це математичне формулювання комп'ютерної постановочній задачі дає нові потужніші схеми відновлення, звані Модульними схемами, для о більшого числа пошкоджених комп'ютерів, ніж схеми [Голомбо 10]. Усі ці алгоритми (Log, Ощадливий, Голомбо і Модуль) гарантують оптимальність певного числа пошкоджених комп'ютерів в кластері. У [8] ми обчислюємо кращі можливі схеми відновлення для будь-якого числа пошкоджених комп'ютерів. Через обчислювальну складність задачі, знахідки, такої схеми відновлення − комплексна задача. Ми тільки можемо подати оптимальну схему відновлення для максимуму 21 комп'ютера у кластері (n ≤ 21). Тут ми подали нові схеми відновлення, які засновані на Оптимальних Лінійких Голомбо і гарантують оптимальну поведінку для набагато більшого ряду пошкоджених вузлів.
Схеми відновлення 4.1. Нижчий MV межі Функція MV(k) − нижня межа для будь-якої схеми відновлення: Визначення 1. Ми говоримо, що схема відновлення оптимальна, якщо q пошкоджених вузлів, щільні аж до q з MV векторної межі, тобто для L (n, k, R) = MV (k) k = 1, …, q. Для двох пошкоджених вузлів в кластері MV (2) = 2, Поки схема відновлення оптимальна для двох пошкоджених вузлів. Коли s 1 = s 2 схеми відновлення не оптимальна.
4.2. Послідовність S Визначення 2. Збійний маршрут Ci ми визначаємо послідовністю: < (s1+s2+...+сі) (s2+...+сі),..., сі>. J−тий вхід в послідовність Ci, який ми означаємо Ci, j. Потім є наступні збійні маршрути: збійний маршрут C1: s1 збійний маршрут C2: (s1 + s2), s2 збійний маршрут C3: (s1 + s2 + s3), (s2 + s3) s3, тобто C3, 2 = (s2 + s3). Задача виявлення послідовності, яка оптимальна аж до k, пошкодила вузли, які ми формулюємо як зазначено нижче: Знайдемо послідовність додатніх цілих чисел таких, що: 1. сума елементів в послідовності є менш ніж рівний n, тобто 2. 3. перші маршрути l вимкненьи не перетинаються, тобто значення дорівнює:) 4. наступні збійні маршрути попередні збійні маршрути, тобто
Приклад послідовності Нехай n = 19 і S = <1,3,2,5,2,5>. Ми подали послідовність і її збійні маршрути, як трикутник (подивіться Мал. 4). Жирні номери − усі різниці. Перші три збійні маршрути (C1 ={1}; C2 ={4,3}; C3 ={6,5,2}) не перетинаються. У наступних збійних маршрутах знаходяться найменше 3 унікальних значень. Це просто, щоб вичислити, що для l = 3 число пошкоджених вузлів меьше, ніж 9. Отже ця послідовність має бути оптимальна аж до щонайменше пошкоджених 8 вузли.
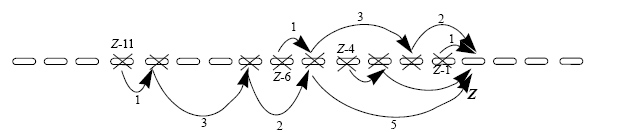
Мал. 4 Трикутне представлення послідовності Мал. 5 представляє схему, користуючись послідовністю <1,3,2,5,2,5>. Навантаження на Z зростає, коли усі вузли від збійного маршруту вимикаються. У цьому прикладі навантаження зростає на Z – C 1, 1 = Z – 1, коли ламаються, вузли від збійного маршруту C2, тобто і, вузли від збійного маршруту C3 тобто Z – C 2,1 = Z – 4, і Z – C 2, 2 = Z – 3 вузли від збійного маршруту C4. Після дев'яти пошкоджених вузлів навантаження на Z зростає в чотири рази. Якщо у збійному маршруті C4 тільки два вузли вимкнулися, то навантаження на Z повине зростати тільки в три рази. Від вектору межі ми знаємо, що MV(9) = 4, так схема не буде оптимальна для дев'яти вузлів в нашому прикладі. Проте, MV(8) = 4 і що схемна гарантує оптимальність для 8 пошкоджених вузлів.
Мал. 5 Приклад використання послідовності<1,3,2,5,2,5>. Теорема 1: Схема відновлення сконструювала в деякому відношенні, коли перші збійні маршрути Cx для 1 ≤ x ≤ l не перетинаються і наступні збійні маршрути Cy для мають Доказ: Спочатку ми покажемо, що, якщо перші збійні маршрути Cx для 1 ≤ x ≤ l не перетинаються потім схема відновлення гарантує оптимальність, поки Коли x вузли вимкнулися Це означає, що процес передавав усі вузли 1. Z – s 1 Z – C 1, 1 2. Z –(s 1 + s 2) Z – s 2 Z – C 2, 1, Z – C 2,2 3. Z –(s 1+ s 2+ s 3) Z –(s 2 + s 3) Z – s 3 = Z – C 3, 1, Z – C 3,2, Z – C 3, 3 … х.
Перші маршрути l вимкнень не перетинаються. Це означає, що не більш ніж олин вузол не включається один із списків. Отже, найгірший випадок є, коли вузли в найкоротших списках мають ушкодження, наприклад для k = 3 найгірший випадок відбувається, коли вузол від збійного маршруту зламався, а потім коли вузли від збійного маршруту вимкнулися. Це означає, що після трьох вимкнень навантаження на вузол Z має три роботи. Нижня межа, оптимальності доведена. Так само для k = 6 найгірший випадок відбувається, коли вузли від Z – C 1 Z – C 2, і Z – C 3 вимкнулися. Це означає, що шість вузлів мають пошкодження і робота на вузол Z − чотири. Нижня межа і оптимальність доведені. Число різних вузлів у збійних маршрутах рівне і тому найгіршиф випадок відбувається, коли вузли від Z – C 1, Z – C 2,…, Z – Cl, вимкнулися. Оскільки Збійний маршрут Z – C l + 1 порівняно значення l унікальний з попередніми збійними маршрутами, тобто має одне значення, яке входить в один з попередніх збійних маршрутів. Це означає, що процес від вузла передаватиме l нові вузли, щоб закінчитися на вузол Z і однин вузол, який вже вимкнувся. Коли тільки вузли вимкнулися від збійного маршруту Cl +1, потім процес від вузла не закінчуйться на вузлі Z і навантаження на Z буде все ще оптимальне. Аналогічно, вузли від збійного маршруту Cl +2 можуть вимкнутися, щоб гарантувати оптимальність для
Регулярна схема відновлення У цій статті ми головним чином розглядаємо регулярні схеми відновлення, коли усі списки мають таку ж структуру, засновану на одному списку (R 0) відновлень. Список відновлень, який ми конструюємо від послідовності відстані S: R 0 =<0, s 1, s 1 + s 2, s 1 + s 2 + s 3, …, s 1+…+ sn – 1>. Потім схеми відновлення конструюються як: Ri ={(r 0 + i)mod n, …,(rn + i)mod n }для, 0≤ i < n де ri = s 1+…+ si є i−та позиція у векторі R0. Наприклад, ми дали наступну регулярну схему відновлення дану вектором: R 0 = <0, 1, 3, 5>: R0: 1, 3, 5 R1: 2, 4, 0 R2: 3, 5, 1 R3: 4, 0, 2 R4: 5, 1, 3 R5: 0, 2, 4 де Ri − список відновлень для комп'ютера номер i. Тут, послідовність S = <1,2,2>. Перший нуль у векторі залишається номером комп'ютера. Для ясності, коли описуємо списки відновлень, ми нехтуємо номер комп'ютера. Кількість регулярних схем відновлення з довжиною n (n комп'ютери) означають R(n). Там (n – 1)! явно відмінні такі послідовності з n комп'ютерами, тому R (n) = (n – 1)! .
|
||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-22; просмотров: 285; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.183.77 (0.017 с.) |



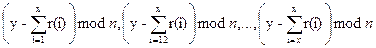


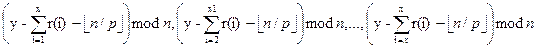
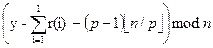

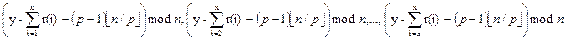
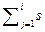 j (i=1,…,n-1) − відстань між пошкодженим вузлом і вузлом на якому процес треба знову почати в i−тому кроці. Нехай потім R0 є списком відновлень просес 0 (виконуючи на комп'ютері 0). Список відновлень, від якого ми конструюємо послідовність S: R 0 =<0, s 1, s 1 + s 2, s 1 + s 2 + s 3, …, s 1+…+ sn – 1>. (ми повертаємося до цього в Секції 4.4)
j (i=1,…,n-1) − відстань між пошкодженим вузлом і вузлом на якому процес треба знову почати в i−тому кроці. Нехай потім R0 є списком відновлень просес 0 (виконуючи на комп'ютері 0). Список відновлень, від якого ми конструюємо послідовність S: R 0 =<0, s 1, s 1 + s 2, s 1 + s 2 + s 3, …, s 1+…+ sn – 1>. (ми повертаємося до цього в Секції 4.4)

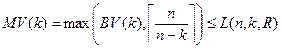 для всіх k = 1, 2, …, p [12]. Тут L (n, k, R) − навантаження на найбільш завантаженому комп'ютері в кластері з використанням n комп'ютерів схема відновлення R, коли сама несприятлива комбінація k комп'ютерів вимкнена. Векторна BV зростає і містить точно k входи, це дорівнює k ≥ 2 J−тий вхід в BV дорівнює
для всіх k = 1, 2, …, p [12]. Тут L (n, k, R) − навантаження на найбільш завантаженому комп'ютері в кластері з використанням n комп'ютерів схема відновлення R, коли сама несприятлива комбінація k комп'ютерів вимкнена. Векторна BV зростає і містить точно k входи, це дорівнює k ≥ 2 J−тий вхід в BV дорівнює 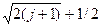 . Отже BV =<2, 2, 3, 3, 3, 4, 4, 4, 4, 5, …>. Номери зростають
. Отже BV =<2, 2, 3, 3, 3, 4, 4, 4, 4, 5, …>. Номери зростають 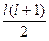 один в вхід для l ≥ 1, так як
один в вхід для l ≥ 1, так як 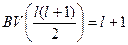 .
.
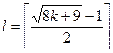 (ми повертаємося до цього в Секції 5)
(ми повертаємося до цього в Секції 5)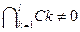 (тобто число унікуму
(тобто число унікуму
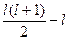 мають в найменших цінностях l унікуму порівняв
мають в найменших цінностях l унікуму порівняв для
для  .
.
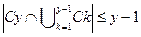 ) гарантує оптимальність, коли найбільше
) гарантує оптимальність, коли найбільше  , просес z (0 ≤ z < n) буде в i−тому кроці закінчуються на вузлі (1 ≤ i ≤ x). Це означає, що процес, який закінчується на вузлі Z після i кроків був спочатку розподілений для вузлі
, просес z (0 ≤ z < n) буде в i−тому кроці закінчуються на вузлі (1 ≤ i ≤ x). Це означає, що процес, який закінчується на вузлі Z після i кроків був спочатку розподілений для вузлі  і цей процес пройшов наступні вузли, перед тим, як досягти вузла Z.
і цей процес пройшов наступні вузли, перед тим, як досягти вузла Z. , для усіх, де Ci, j − збійний маршрут для i−того входу в послідовність S і j−того входу у збійний маршрут. Списки нижче за показане x можливі послідовності вузлів, яким треба вимкнутися для того щоб закінчитися додатковий процес на вузлі Z, тобто, якщо вузол ламається процес закінчиться на вузолі Z.
, для усіх, де Ci, j − збійний маршрут для i−того входу в послідовність S і j−того входу у збійний маршрут. Списки нижче за показане x можливі послідовності вузлів, яким треба вимкнутися для того щоб закінчитися додатковий процес на вузлі Z, тобто, якщо вузол ламається процес закінчиться на вузолі Z.
 , оптимальність доведена.
, оптимальність доведена.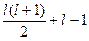 збійних вузлів, тому що Cl +2 порівняно значення l унікальне. Потрібно
збійних вузлів, тому що Cl +2 порівняно значення l унікальне. Потрібно  зібрати маршрути з унікальними значеннями l, порівняно з попередніми вимкненим. Отже схема відновлення, коли перші маршрути l вимкнені і не перетинаються наступна
зібрати маршрути з унікальними значеннями l, порівняно з попередніми вимкненим. Отже схема відновлення, коли перші маршрути l вимкнені і не перетинаються наступна 


