
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Ощадливі Схеми Відновлення і Схеми Відновлення ГоломбоСодержание книги
Поиск на нашем сайте
Зараз ми опишемо ощадливі схеми відновлення і схеми відновлення Голомбо. Ці схеми відновлення оптимальні для більшого ряду важливих випадків, але результати не роблять навантаження балансуючим, коли відбувається “обгорта по колу”. Ми починаємо з визначення R0, тобто списку відновлень для процесу нуль: r(x) = min{ j є N +} таке, що для усіх a1, a2, b1, b2, які виконують умови (1 ≤ a1 ≤ b1 ≤ x) і (1 ≤ a2 ≤ b2 ≤ x) і ((a1 ≠ a2) чи (b1 ≠ b2 )) ми маємо Якщо Усі інші списки відновлень виходять з R0, користуючись Ri(R0(x) + i) mod n. У визначенні R0 ми користуємося вектор довжини кроку r. важлива властивість в ощадливsq схемs відновлення є, що усі суми послідовностей, Від визначення вище ми бачимо, що для великих значень n (тобто n > 289), перші 16 елементів в R0 для ощадливої схеми відновлення є: 1, 3, 7, 12, 20, 30, 44, 65, 80, 96, 122, 147, 181, 203, 251, 289. Для n = 16, R0 = {1, 3, 7, 12, 2, 4, 5, 6, 8, 9, 10, 11, 13, 14, 15}. У [6] ми довели, що ощадлива схема відновлення оптимальна, поки x комп'ютери чи менше вимкнулися, де x = max(i), таке, що R0(i)< m. Окремий випадок ощадливої схеми відновлення − послідовність названа лінійкою Галом ба з n позначками, якиа визначається як послідовність додатніх цілих чисел 0 = d 1< d 2 <… < dn таких, що усі Нехай GR0j є списком відновлень Голомбо для процесу нуль в кластері з j комп'ютерами. Це містить оптимальну лінійку Голомбо з сумою меншою ніж або рівною j і залишок − номери аж до j −1. Наприклад для процеса нуль в кластері з 12 комп'ютерів, які ми маємо: GR0, 12={1,4,9,11,2,3,5,6,7,8,10}. Усі інші списки відновлень виходять з GR0 j,використовуючи GRi, j (x) = (GR 0, j (x) + i) mod (j + 1) для усіх i ≤ j. Окремий випадок OGR − досконала лінійка Голомбо, яка існує, де там є точні відмінності Це означає, що немає ніякої "прогалини " в представленні трикутника. Галом ба взагалі. [1] доводять, що немає ніяких досконалих лінійок Голомбо, коли n > 4. У формулюванні, яким можуть управляти циклічні переходи лінійки Голомбо, є проігноровано − ситуації, коли повне число стрибків для процесу більше, ніж число комп'ютерів в кластері. Наступне формулювання звертає на це увагу: Отримавши число (n) ми хочемо знайти щонайдовшу послідовність додатніх цілих чисел таке, що сума і суми усіх послідовностей (, у тому числі послідовності довжини один) модуль n унікальні. Модульна Схема Відновлення Модульна−n послідовність − послідовність додатніх цілих чисел {аn}, де жодні дві чіткі пари { ai, aj }, { ak, al } для i > j і k > l номерів від послідовності мають той же модуль різниці n, для усіх, де l – довжина послідовності. Наприклад, для l = 4, {1,6,3,10}, {2,1,6,9} і {3,7,9,8} – приклади модульної послідовності−11. мал.. 4 показує з усіма різницями модуля. (перший нуль не враховується до довжини послідовності) Модульна лослідовність використовується як перші значення в списку відновлення для комп'ютера номер нуль в кластері з n комп'ютерами. Інша частина списку відновлень заповнена номерами, що залишилися, аж до n −1. 0 1 6 3 10 1 5 8 7 6 2 4 3 9 Мал.. 4 модульна послідовність для l = 5 і n = 11 з усіма різницями. Нехай MR0,n є модульним списком відновлень для процесу нуль в кластері з n комп'ютерами пронумерованого від нуля до n −1. Потім для n = 11 (і отже l = 4), який ми маємо: MR0, 11 ={1,6,3,10,2,4,5,7,8,9}, наприклад перша частина в MR0, 11 − модуль−11 послідовності для довжини 4 і інша частина MR0, 11 − номери, що залишилися, n −1. Це означає, що, якщо комп'ютер номер нуль зламаний, потім процес треба знову почати спочатку на комп'ютері один, завершено комп'ютером шість, завершено комп'ютером три, і так далі. Стрибки від пошкоджених комп'ютерів дорівнюють різницям від послідовності модуля. Схему відновлення модуля отримує модульний список відновлень для процесу i у кластері з n комп'ютерами: MRi, n = {(i + MR0, n(1)) mod n, (i + MR0, n(2)) mod n, (i + MR0, n(3)) mod n,.,(i + MR0, n (n −1)) mod n}, де MR0, n(i) − i−ітий вхід в MR0, n. Наприклад, для n = 4, який ми маємо: MR0, n = {1,3,2}, MR1, n = {2,0,3}, MR2, n ={3,1,0}, і MR3, n = {0,2,1}. Число комп'ютерів в кластері визначає яка схема різного модуля придатна для використання. Наприклад, для кластерві з 11, 12, 13, 14, 15, 16, 17 (z) комп'ютерів ми користуємося схемами модуля з довжиною 4 модуля 11. Відновлення складає список особливо для комп'ютерів − конструкція яких зазначена нижче: MRi, z = {(i + MR0, n(1)) специфікатор вирівнювання z, (i + MR0, n(2)) mod z, (i + MR0, n(3)) mod z,.,(i + MR0, n (n −1)) mod z}, де MR0, n(i) − i−іте вхід в MR0, n. Наприклад, для z = 5, який ми маємо: MR0, z = {1,3,2}, MR1, z = {2,4,3}, MR2, z ={3,0,4}, MR3, z = {4,1,0}, і MR3, z = {0,2,1}. Мал. 5 подає приклад списку відновлення в кластері з 11 комп'ютерів, коли комп'ютер нуль зламався.
Теорема 1: Модульна схема відновлення оптимальна, поки x комп'ютери або менше вимкнулися, де x = max(i), таке, що MR0, n(i)< n. У наступному доказі, усі модулі номерів n − будь-якиі з додатніх цілих чисел 0, 1,..., n − 1, означають комп'ютери, перераховані таким чином. Доказ: Нехай y (0 ≤ y < n) є найюільш завантаженим комп'ютером, коли x комп'ютери вимкнулися, де x = max(i), таке, що M0, n(i)< n.
Мал. 5 Модуль−11 список відновлення для процесу нуль Коли x комп'ютери вимкнулися, просес z (0 ≤ z < n) буде в i−ітому кроці закінчуються на комп'ютері 1. 2. 3. … х. Від визначення послідовності модуля ми знаємо, що усі суми послідовностей модуль n унікальні. Це означає, що ніякий комп'ютер не включається в більш ніж один з спискыв. Отже, найгірший випадок є ясно, коли комп'ютери в найкоротших списках мають ушкодження, наприклад для x = 3 найгырший випадок відбувається, коли комп'ютер: Ми бачимо, що ніякий комп'ютер не включається у більш ніж один з x перших списків. Враховуючи попередні результати ми знаємо, що схема оптимальна, поки ніякий комп'ютер не входить в два такі списки. Теорема слідує.
|
||||
|
Последнее изменение этой страницы: 2016-06-22; просмотров: 322; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.109.141 (0.006 с.) |

 .
. , потім
, потім  , інші R 0(x) = min{ j є N+ – { R 0(1) ,…,R 0(x − 1)}}. (n − ряд ідентичних комп'ютерів в кластері)
, інші R 0(x) = min{ j є N+ – { R 0(1) ,…,R 0(x − 1)}}. (n − ряд ідентичних комп'ютерів в кластері) є унікальний, тобто
є унікальний, тобто  , коли (1 ≤ a1 ≤ b1 ≤ x) і (1 ≤ a2 ≤ b2 ≤ x) і ((a1 ≠ a2) або (b1 ≠ b2)).
, коли (1 ≤ a1 ≤ b1 ≤ x) і (1 ≤ a2 ≤ b2 ≤ x) і ((a1 ≠ a2) або (b1 ≠ b2)). різниці dj – di, з i < j чіткі. Найкоротша лінійка Голомбо для цього ряду позначок є під назвою Оптимальна Лінійка Голомбо (OGRs). Від схеми відновлення Голомбо для кластера з j комп'ютерами виходить список відновлень Голомбо, який містить дві частини. Перша частина складається з оптимальної Лінійки Голомбо з сумою менше або дорівнює j і з другої частини заповненлї номерами, що залишилися, аж до j −1.
різниці dj – di, з i < j чіткі. Найкоротша лінійка Голомбо для цього ряду позначок є під назвою Оптимальна Лінійка Голомбо (OGRs). Від схеми відновлення Голомбо для кластера з j комп'ютерами виходить список відновлень Голомбо, який містить дві частини. Перша частина складається з оптимальної Лінійки Голомбо з сумою менше або дорівнює j і з другої частини заповненлї номерами, що залишилися, аж до j −1.
 . R(j) ми означаємо кроки від пошкодженого комп'ютера, які є різницями в послідовності модуля. Це означає, процес що закінчується на комп'ютері y після i кроків був спочатку розподілений для комп'ютера
. R(j) ми означаємо кроки від пошкодженого комп'ютера, які є різницями в послідовності модуля. Це означає, процес що закінчується на комп'ютері y після i кроків був спочатку розподілений для комп'ютера  ; і цей процес передав
; і цей процес передав  перед тим, як він досяг комп'ютера y. Списки x показані нижче − можливі послідовності комп'ютерів, яким треба виключитися для того, щоб додатковий процес закінчитився на комп'ютері y, тобто, якщо комп'ютер (y−r(1)) mod n у вимкнений один додатковий процес закінчиться на комп'ютері y, якщо mod комп'ютер (y−r(1) −r(2)) n і (y−r(2)) mod n − додатковий процес закінчиться на комп'ютері y, і так далі.
перед тим, як він досяг комп'ютера y. Списки x показані нижче − можливі послідовності комп'ютерів, яким треба виключитися для того, щоб додатковий процес закінчитився на комп'ютері y, тобто, якщо комп'ютер (y−r(1)) mod n у вимкнений один додатковий процес закінчиться на комп'ютері y, якщо mod комп'ютер (y−r(1) −r(2)) n і (y−r(2)) mod n − додатковий процес закінчиться на комп'ютері y, і так далі.




 зламавля, а потім коли
зламавля, а потім коли 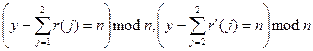 зламалися. Так само для x = 6 найгірший випадок відбувається, коли комп'ютер:
зламалися. Так само для x = 6 найгірший випадок відбувається, коли комп'ютер:  вимкнулися, а потім коли комп’ютер
вимкнулися, а потім коли комп’ютер 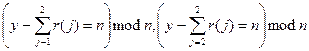 вимкнулися, а потім коли комп’ютер
вимкнулися, а потім коли комп’ютер 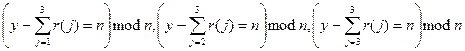 вимкнулися.
вимкнулися.


