
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Використання лінійок Голомбо для оптимальних відновлюючих системах в Розподілених Обчисленнях толерантних до помилокСодержание книги
Поиск на нашем сайте
Каміла Клоновська, Ларс Люмберг, Хаккан Леннерстад Робота 17-го Інтернаціонального симпозіуму Паралельних та Розподілених обчислень IPDPS 2003, Ніса, Франція, квітень 2003
Резюме Кластери і розподілені системи дозволяють толерантність до помилок і високу продуктивність завдяки спільному використанню. Коли усі комп'ютери ввімкнені і працюють, ми захотіли б, щоб навантеження було порівну розподілене серед комп'ютерів. Коли один або більше комп'ютерів ламаються, навантаження яке було на цих комп'ютерах має бути перерозподілене на інші комп'ютери в кластері. Перерозподіл визначає схема відновлення. Схема відновлення повинна тримати навантаження, найоптимальніше, як тільки можливо, навіть, коли найнесприятливіші комбінації з комп'ютерів ламаються, тобто ми хочемо оптимізувати найгіршу з можливих варіантів поведінку. У цій статті ми визначаємо схеми відновлення, які оптимальні для ряду важливих випадків. Ми також показуємо, що задача виявлення оптимальних схем відновлення відповідає математичній задачі під назвою Лінійка Голомбо. Вони забезпечують оптимальне відновлення схеми для аж до 373 комп'ютерів в кластрі. Вступ Єдиний шлях отримання високої придатності і толерантності до помилки - виконувати додаток на кластерній або розподіленій системі. Є головний комп'ютер, який виконує додаток за нормальних умов і вторинний комп'ютер, який приймає задачу, коли головний комп'ютер вимикається. Можливо, також є третій комп'ютер, який приймає задачу, коли головний і вторинний комп'ютери - вимкнені, і так далі. Порядок в якому комп'ютери використані названий порядком відновлення, отриманий списком відновлення. Багато кластерних виконувачів підтримують цей вид виправлення помилок, наприклад: Sun Cluster [14] MC/ServiceGuard (HP) [9], TruCluster (DEC) [15], HACMP (IBM) [1], and MSCS (Microsoft) [10,16]. Перевага користування кластерами, окрім толерантності до помилок, − навантаження, розподілене між комп'ютерами. Коли усі комп'ютери працюють, ми захотіли б, щоб навантаження було розподілене порівну. Проте навантаження на деяких комп'ютерах буде, зростати, коли один або більше комп'ютерів вимикаються, але і за цих умов, ми захотіли б розподілити навантаження якомога порівну на комп'ютерах, що залишилися. Поширення навантаження, коли комп'ютер вимкнений вирішене порядком відновлення процесів, що проходять на дефолтному комп'ютері. Безліч усіх порядків відновлення є так званою схемою відновлення, тобто поширенням навантаження у разі коли один або більше дефектів визначається схемою відновлення. Задача виявлення оптимальних (або навіть кращих) схем відновлення раніше не була вивчена іншими дослідниками. У попередній статті [8] ми визначили схеми відновлення, які оптимальні для деяких випадків. У цій статті ми подали нові схеми відновлення, для яких оптимальним є значно більше число пошкоджених комп'ютерів. Деякі з схем засновані на так званій лінійці Голомбо, яка була використана в радіоастрономії.
Формулювання задачі Ми розглядаємо кластер з n ідентичних комп'ютерів. Є один процес на кожному комп'ютері. Робота − рівномірно розділена на ці n процеси. Є список відновлень асоційований з кожним процесом. Цей список визначає, де процес треба знову почати, якщо поточний комп'ютер вимкнений. На мал. 1 показана така система для n = 4. Ми стверджуємо що процес переміщається назад, як тільки комп'ютер повертається знову. У більшості кластерних систем це може бути встановлено користувачем [9,14,15], тобто в деяких випадках один може не хотіти автоматичного перерозподілу процесів, коли помилковий комп'ютер повертається знову. Ліва сторона фігури показує систему за нормальних умов. У цьому випадку, є один процес на кожному комп'ютері. Списки відновлень також показані; один список для кожного процесу. Сукупність усіх списків відновлень названі схемою відновлення. Права сторона Мал. 1 показує сценарій, коли головний комп'ютер вимкнений. Список відновлення для нульового процесу показує що він повинен бути запущений на комп’ютері один, доки нульвий комп’ютер вимкнений. Якщо комп'ютер один також ламається, нульовий процес виконується на комп'ютері два, який є другим комп'ютером в списку відновлень. Перший комп'ютер в списку відновлень процесу один – нульовий комп’ютер. Проте, коли нульовий комп’ютер вимкнений, процес один буде знову розпочатий на комп'ютері три. Тому, якщо комп'ютери нуль і один не прюють, є два процеси на комп'ютері два (процесb нуль і два) і два процеси на комп'ютері три (процеси один і три).
Мал. 1 Виконання додатка в кластері з чотирьох комп’ютерів Якщо комп’ютери нуль і один вимкнені, максимальне навантаженяя на кожному з тих що залишилися − двічі більше за нормальне навантаження. Це добрий результат, навантаження оптимально розподілене, як тільки це можливо. Проте, якщо комп'ютер нуль і два вимкнені, є три процеси на комп'ютері один (процеси нуль, один і два), тобто максимальне навантаження в три рази більше за нормальне на найзавантаженішому комп'ютері. Тому, для схеми відновлення в Мал. 1, комбінація вимкнених кмп’ютерів нуль і два, несприятливіша, ніж комбінація вимкнених кмп’ютерів нуль і один. Наші результати також дійсні, коли є системи n зовнішнього живлення даних всередині кластера, наприклад один телекомунікаційний центр постачає дані для кожного комп'ютера у кластері. Якщо комп'ютер віключається, центр повинен направити свої дані на деякий інший комп'ютер в кластері, тобто повинен бути "списком відновлень", що асоціюється з кожним обмінним центром. Несправна команда може альтернативно бути владнана списком відновлення що складає список на рівні протоколу комунікації, наприклад IP [12]. У такому разі, переадресовувавши комунікацію до іншого комп'ютера є прозорим для обмінного центру. Багато кластерних виконувачів пропонують не лише щоб користувач визначив дані схеми відновлення тут, але і динамічне навантаження, що балансує схеми у разі вимкнення комп’ютера. Непередбачувана поведінка в найгіршому випадку і відносно числа часу затримки переходу такої динамічної схеми є, проте, неприваблива у багатьох додатках реального часу. Також зовнішні системи не можуть користуватися динамічним навантаженням, що балансує схеми, коли їм треба вибрати новий вузол, коли первинне місце призначення для їх продукції не відповідає. Тому результати, представлені тут, дуже релевантні для систем, де кожен вузол має його власну мережеву адресу. Крупно розділені кластери повинні знати, де робота піде, якщо поточні комп'ютери вимкнуться. Причина, ми переконані, в тоиу що усі необхідні дані копіюються в комп'ютер, на якому робота починається заново після вимкнення і для великих кластерів ми не можемо копіювати усі дані в кожен вузол в кластер. Це означає, що ми повинні користуватися статичними схемами крупно розділених кластерів. Знайти хороші схеми відновлення − фундаментальна задача в розподіленних і кластерних системах. Ми припускаємо, що робота, що виконується кожним з n комп'ютерів, має бути переміщена, як одна атомна одиниця. Приклади − системи, де уся робота, що виконується комп'ютером робиться від однієї зовнішньої системи або коли усю роботу виконує один процес чи системи, де зовнішньою комунікацією управляє IP протокол [2] (у цьому випадку увесь зовнішній рух за однією мережевою адресою спрямовується за мережевою адресою як одна атомна одиниця). Попередні результати підсумовуються в Секції 3. У Секції 4 ми покращуємо попередні визначення ощадливих схем відновлення, які оптимальні також, коли значно більше число комп'ютерів вимикається. Оптимальна схема відновлення яка виходить з лінійки Голомбо представляється в Секції 5. Укладення представляється в Секції 6.
Загальна нижчня межа B Ми починаємо з представлення деяких систем позначень. Розглянемо кластер з n комп'ютерами. Нехай L (n,x, { c 0,…, cx -1}, RS) (n > x) означають навантаження на найбільш сильно завантажений комп'ютер коли комп'ютери c0,., c x −1 вимикаються і використовується схема відновлення RS. L (4,2,{0,1}, RS) = 2 для прикладу в Мал. 1, але L (4,2,{0,2}, RS) = 3. Нехай L (n, x, RS)= max L (n, x, { c0,., cx −1}, RS) для усіх векторів { c0,., cx −1}, тобто для усіх комбінацій x комп'ютери, що вимикаються. Тому, L (n, x, RS) визначає найгіршу поведінку. Для схеми відновлення на Мал. 1, L (4,2, RS) = 3. Схема відновлення повинна поширювати навантаження як можна порівну для будь-якого числа вимкнених комп'ютерів x. Маленькі значення x звичайніші, ніж великі значення x. Ми позначаємо { L (n, 1, RS),., L (n, n− 1, RS)} як V (L (n, RS)) Відмітьте, що VL − вектор довжина n−1 ми ігноруємо випадок, коли усі n комп'ютери вимкнені. Ми говоримо, що V (L (n, RS)) послідовно меньше, ніж V(L( n, RS')), якщо входи є ідентичні аж до порядкового y, і для цього показника міри значення V (L (n, RS)) меньше, ніж V (L (n, RS')). Отже, для деяких y < n, який ми маємо 1. L(n, y, RS)< L(n, y, RS') і 2. L(n, z, RS) = L(n, z, RS') для усіх z < y. Якщо y = 1, цього досить для L (n, y, RS)< L (n, y, RS'). Якщо V (L (n, y, RS)) послідовно меньше, ніж V(L(n, y, RS')), ми розглядаємо RS як кращу схему відновлення, ніж RS', наприклад для V = V (L (n, y, RS)) ={2,2,3,3,3,4,4} і V' = V (L (n, y, RS')) ={2,3,3,3,3,3,3} V послідовно меньше, ніж V'. Поведінка коли декілька комп'ютерів вимикаються вища по пріоритетах порівняно з тим, коли багато комп'ютерів вимикаються. Зворотне твердження до " V (L (n, y, RS)) послідовно меньше, ніж V(L(n, y, RS')) " є “ V (L (n, y, RS')) послідовно більше, ніж або дорівнює V (L (n, y, RS)) ". Потім також V (L (n, y, RS)) і V(L(n, y, RS'))ідентичні, або V(L(n, y, RS) ) послідовно меньше ніж V (L (n, y, RS')). Нехай VL = min V (L (n, RS)), де мінімум прийнятий усіма схемами відновлення RS. Ми заздалегідь визначили нижчу межу B на VL, тобто B ≤ VL (B – вектор довжини n −1), і для n ≤ 11, ми визначили схему відновлення RS таку, що V (L (n, RS)) = B [8]. Ми посилаємося на такі схеми відновлення як оптимальні схеми відновлення. Ми маємо також певні схеми відновлення, які оптимальні, коли у більшості log2n комп’ютерів вимикаються. Потім ми визначаємо вектори (BV): BV довжина l= 2+3+4+.+ k має наступну послідовність: <2,2,3,3,3,4,4,4,4,5,5,5,5,5,., k, k,., k > (векторні кінці з k входами зі значенням k). Наприклад, BV довжини 2+3+4+5=14 виглядає як: <2,2,3,3,3,4,4,4,4,5,5,5,5,5>. Ми можемо просто вичислити n-тий вхід в послідовність за допомогою формули Ми зараз розширюємо визначення межі векторів, щоб включати вектори будь-якої довжини беручи довільну BV і урізаючи її до позначеної довжини, наприклад BV довжини 12 виглядає як: <2,2,3,3,3,4,4,4,4,5,5>.
Теорема 1: VL(i) ≥ n/(n-i) (VL(i) − номер входу i в VL). Доказ:, Якщо i комп'ютери вимикаються, є i процеси, для яких має бути розподілений залишок n−i комп'ютерами. Найкраще на що можна сподіватися що отримане навантаження n /(n−i) процесами буде на найбільш сильно занавантаженому комп'ютері.
Теорема 2: BV послідовно меньша, ніж VL, тобто, BV і VL ідентичні аж до порядкового y, і BV (y)< VL(y). Доказ: З Теореми 1 ми знаємо що BV (n− 1) < n ≤ VL(n − 1), якщо n > 3. Отже BV і VL не можуть бути ідентичними. Ми користуємося доказом протиріччям. Припустимо, що VL послідовно меньше, ніж BV. У цьому випадку є y таке, що BV (x) = VL(x < y) і BV (y)> VL(y). Очевидно, VL (y− 1) ≤ VL(y). BV тільки зростає у входи xk = k (k −1)/2, для k = 2, 3, 4,…, тобто x2 = 1, x3 = 3, x4 = 6,. Тому, різниця між VL і BV повинна відбуватися у вході xk, тобто y = xk. Це означає що, VL(xk)< BV (xk) = k для деяких xk. Якщо k = 2 (xk = 1), один комп'ютер вимикппється, і очевидно VL(1) = 2, тобто VL(1) = BV (1). Починаючи з VL(2) = 2 ми знаємо, що два списоки відновлення не можеть до одного і того ж комп’ютера. (Якщо два списки, що відповідають процесам c1 і c2, починаються з того ж комп'ютера c3, буде три процеси на комп'ютері c3, якщо комп'ютери c1 і c2 вимимкаються.) Якщо k = 3 (xk = 3), три комп'ютери вимикаються. Виходячи з того що усі списки відновлень починаються з різних комп'ютерів, має бути щонайменше одна пара списків відновлення l1 (відповідальний за обробку c1) і l2 (відповідальний за обробку c2) такі, що комп'ютер c3 перший в l1 і c3 − друга альтернатива в l2. Якщо c1, c2 і перша альтернатива в l 2 вимикається, буде три процеси на c3. Тому, VL(3) = 3. Починаючи з VL(5) = 3, ми знаємо два списки відновлень мають той же комп'ютер, як другу альтернативу. Якщо два списки відповідальні за c1 і c2 мають той же комп'ютер c3, як другу альтернативу, тоді будуть чотири процеси на комп'ютері c3, якщо комп'ютери c1, c2, перша альтернатива в l1 і l2 і комп'ютер з c3 як перша альтернативна вимкнулись. Якщо k = 4 (xk = 6), шість комп'ютерів вимикаються. Починаючи з початку усіх списків відновлень з різними комп'ютерами і мають різні комп'ютери як другу альтернативу, там повинна знаходитися що найменше одна трійка відновлення яка складає список l1, l2 і l3 така, що комп'ютер c4 перший в l1 і друга альтернатива в l2 і третя альтернатива в l3. Якщо комп'ютери c1, c2, c3, перша альтернатива в l2, перша і друга альтернатива в l3 вимикаються, буде оброблятися чотири процеси на c4. Тому, VL(6) = 4. Починаючи з BV (9) = 4, ми знаємо, що два списки відновлень мають той же комп'ютер, як третю альтернативу. Якщо два списка відповідно до c1 і c2 мають той ж комп'ютерний c3, як третю альтернативу, буде оброблятися чотири процеси на комп'ютері c3, якщо комп'ютери c1, c2, перша альтернатива в l1 і l2 і комп'ютер c3 як перша альтернативна вимкнулися. Ця процедура може бути повторною для усього k. З цього ми можемо зробити висновок, що немає ніякого k такого, що, VL (xk)< k, де xk = 2+3+4+.+ k −(k −1). Тому, BV є послідовно меньше, ніж VL. Опираючись на теореми 1 і 2, ми визначаємо В(і)=max (BV(i),n/(n−i)) Ощадні Схеми Відновлення Інтуїтивна схема (RS) відновлення − Ri = {(i+ 1) mod n, (i+ 2) mod n, (i+ 3) mod n,., (i+n− 1) mod n }, де Ri − список відновлень для процесу i. Якщо n = 4, який ми отримуємо: R0 = <1,2,3>, R1 = <2,3,0>, R2= <3,0,1>, і R3 = <0,1,2>. Інтуїтивна схема не є оптимальна для n = 4 (у такому разі B(2) = 2 але L (4,2,{0,1}, RS) = 3). Для n = 8, ми знаємо що B(5) = 3 але L (8,5,{0,1,2,3,4}, RS) = 6. Тому, найгірша поведінка інтуїтивної схеми двічі така ж погана як оптимальна схема для n = 8. Ми маємо показник, коли найбільше x = log2n, комп'ютерів вимикається VL(i) = B(i) (i ≤ x) [8]. Якщо ми (для деяких integer y > 1) маємо Це відбувається, коли комп'ютери 0, 1, 2,. x −1 вимикаються, наприклад для y = 3 і отже x = 2 + 3 = 5 ми отримуємо різницю (1+2+3)/3 = 2, коли комп'ютери 0,1,2,3,4 вимикаються. Ми зараз визначимо схему відновлення названу ощадливою схемою відновлення, яка може гарантувати оптимальну поведінку також, коли значно більше ніж log2n комп'ютерів ламаються. Ми покажемо, що ця схема відновлення оптимальна для ряду важливих випадків. Ми починаємо з визначення R0, тобто списоку відновлень для процесу нуль (N = {1,2,3,.}: r(x) = min{ j є N }, таке, що для усього a1, a2, b1, b2, які виконують умови ((1 ≤ a1 ≤ b1 ≤ x) і (1 ≤ a2 ≤ b2 ≤ x) і ((a1 ≠a2) чи (b1 ≠b2))) таким чином, що ми добираємося Якщо Ми отримуємо усе інші списки відновлень від R0, користуючись Ri(R0(x) + i) mod n. У визначенні R0 ми використовуємо вектор довжини кроку r. Важлива властивість в ощадливій схемі відновлення є, що усі суми послідовностей, Від визначення вище ми бачимо, що для великих значень n (тобто n > 289), перших 16 елементів в R0 для ощадливої схеми відновлення є: 1, 3, 7, 12, 20, 30, 44, 65, 80, 96, 122, 147, 181, 203, 251, 289. Для n = 16, R0 = <1, 3, 7, 12, 2, 4, 5, 6, 8, 9, 10, 11, 13, 14, 15>. Ми зараз визначаємо новий вектор довжини x. Цей вектор названий зменшеним кроком довжини вектора (r') і складається з перших x входів у вектор довжини кроку r, де x = max(i), таке, що R0(i)< n. Від визначення ощадливої схеми відновлення ми знаємо, що усі суми послідовностей в r. унікальні. Таблиця 1 ілюструє це для n = 97 призводячи до зменшення вектору довжини кроку 10 (10 = x = max(i), таке, що R0 (i) <n = 97). Теорема 3: Ощадлива схема відновлення оптимальна, поки x комп'ютерів або менше вимкнулися, де x = max(i), таке, що R0(i)< n.
Таб. 2 Усі суми послідовностей зменшення довжини кроку вектора для n=97
Доказ: Нехай y (0 ≤ y < n) буде найбільш завантаженим комп'ютером, коли x комп'ютери мають ушкодження, де x = max(i), таке, що R0(i)< n. Коли x комп'ютери вимкнулися, процес z (0 ≤ z < n) буде в i−тому кроці закінчуються на комп'ютері 1. 2. 3. …
Від визначення r ми знаємо, що усі суми послідовностей,
Порівнюючи це з доведенням Теореми 2 ми бачимо, що перші x входи в B і V (L (n, RS)) − ощадливе відновлення ідентичне (RS = ощадливасхема відновлення, x = max(i) таке, що R0(i)< n). Теорема слідує. Щоб резюмувати наше проблемне формулювання: Отримавши певний ряд комп'ютерів (n) ми хочемо знайти схему відновлення, яка може гарантувати оптимальне поширення навантаження в найгіршому випадку коли більшість комп'ютерів x вимикається, і ми зацікавлені в схемах, що мають максимально велике х. Переглядаючи доведення Теореми 3, ми бачимо, що задача може бути переформульована як: Отримавши число (n) ми хочемо знайти щонайдовшу послідовність позитивних цілих чисел таких що сума послідовності меньша, або дорівнює n і така, що усі суми послідовності (у тому числі послідовності довжини один) унікальні. Ця задача подібна до відомої задачі, описаної Галомбом в 1977, як лінійка [2]. Лінійка, що охоплюєз n позначок і довжиною L вимірює кожну відстань з 1 до L, як відстань між двома позначками на лінійці, у у більшості одного шляху. Комбінаторна задача для того, щоб визначити найкоротшу лінійку для кожного n. Дуальна задача − визначити, найдовшу супровідну лінійку з n позначками і довжиною L, яка знаходила б кожну відстань з 1 до L, як відстань між двома позначками на лінійці, щонайменше в одному наапрямку. Обоє з цих задач мають довгі історії в комбінаторноній літературі [6]. Гарднер [4] назвав ці об'єкти як "лінійку Голомбо", які були широко застовані. Лінійка Голомбо використовується в різноманітних областях як наприклад радіоастрономія, рентгенівське випромінювання, і міріади інших областей наприклад кодування даних і географічний відбір.
Лінійка Голомбо Лінійка Голомбо − послідовність додатніх цілих чисел таких що жодні дві чіткі пари номерів від множини мають ту ж різницю. Ці номери є так званими позначками і відповідають позиціям на лінійному масштабі. Різниця між значеннями яких-небудь двох позначок названа відстанню. Найкоротша лінійка Голомбо для цього ряду марок зветься Оптимальною Лінійкою Голомбо (OGRs) [3]. Пошук OGRs стає важчим, оскільки число марок зростає. Це відомо як NP−завершена проблема [13]. Оптимальна для 19 марок була доведена в обчислювальному відношенні Долласом[4]. OGRs за 20, 21, 22 і близько 23 позначок робить всесвітньо-поширене зусилля в Інтернеті [7, 18]. Задача для великого ряду позначок все ще не розв’язана. Відома OGRs представляється в таблиці в додатку. Приклад представлення OGR з чотирма позначками показується в Мал. 2. Є можливо виміряти відстані: 1, 2, 3, 4 як 1+3, 5, 7 як 5+2, 8 як 3+5, 9 як 1+3+5, 10 як 3+5+2 і 11 як 1+3+5+2, але ми не можемо виміряти відстань 6.
Мал. 2 Представлення лінійки OGR з чотирма позначками Лінійка Голомбо може також бути представлена як трикутник, де кожен номер представляє різницю між парою специфічних номерів. Мал. 3 показує приклад з чотирьох позначок. Перший порядок (над лінією) представляє позначки уздовж лінії такі, що кожна пара позначок вимірює унікальну лінійну відстань. У другому ряду є відстані зважені між позначками розміщеними по два окремо на лінійці. Лінійка з позначками m має m − 1 першу порядкову відмінність, m − 2 другу порядкову відмінность, і так далі, аж до одного m − 1 порядку різниці. Отже, k порядків різниці, ми маємо на увазі різницю позначок де k позиції один від одного.
Мал. 3 Представлення трикутного вигляду лінійки Голомбо
Лінійка Голомбо зазвичай характеризує їх абсолютні відстані, замість відмінностей. Послідовність різниці − послідовність першого порядку обчислень (різниця першого ряду під лінією в діаграмі вище). Нижче лінійка склала би 1−4−9−11 як абсолютні відстані (іноді це пишеться як 0−1−4−9−11, але початковий нуль часто відпадає) і 1−3−5−2 як відмінності. У цій статті ми користуємося системою позначень відмінностей схеми відновлення Голомбо. Проте, ми користуємося системою позначень абсолютних відстаней для списків відновлень Голомбо. У додатку ми надали таблицю з 23 OGRs. Наприклад, зараз найвідоміша лінійка 23-позначок, що характеризується відмінностями наступна: 0−3 − 4−10−44−5−25−8−15−45−12−28−1−26−9−11−31−39−13−19−2−16−6. Ми переформулювали задачу в цій статті: Отримати число (n), до якого ми хочемо знайдіти щонайдовшу послідовність додатніх цілих чисел таких, що сума послідовності є меньша, або дорівнюює n і така, що усі суми послідовностей (у тому числі послідовності довжини один) унікальні. Відколи ця задача еквівалентна до задачі знаходження лінійки Голомбо, ми можемо користуватися результатами лінійки Голомбо. Проте, оптимальні послідовності для великих номерів все ще не відомі. Список відновлень отримується додаванням значень послідовностей − це послідовність з часткових сум. Перша частина списків відновлень складається з лінійки Голомбо, тобто перші x входи для найбільшого x такі, що сума оптимальної послідовності довжини x менша, ніж n. Частина списку відновлень, що залишилася, наповнена залишком номерів (комп'ютерів) аж до n −1. Нехай Gn є лінійкою Голомбо з сумою n + 1 і нехай Gn(x) бути x-вим входом в Gn, наприклад. G12 = <1,4,9,11> і G12 (1) = 1, G12 (2) = 4 і так далі. Нехай потім gn = x число пошкоджених комп'ютерів з оптимальною поведінкою, коли ми маємо n комп'ютерів, наприклад g12 = 4. Для проміжних значень k ми користуємося меншою лінійкою Голомбо, і інша частина списку відновлень наповнена номерами, що залишилися до k −1. Наприклад, наповнюючи номерами, що залишилися, лінійка G12 дає список {1,4,9,11,2,3,5,6,7,8,10} і G18 дає список {1,4,10,12,17,2,3,5,6,7,8,9,11,13,14, 15,16}. Отже, для n = 14 ми користуємося G12, щоб отримати список {1,4,9,11,2,3,5,6,7,8,10,12,13}. Покази таблиці 2, що різниця, в показах числа пошкоджених комп'ютерів для яких ми можемо гарантувати оптимальне поширення навантаження, − у більшості є одним для n = 35, наприклад користуючись схемами відновлення, які засновані на оптимальній лінійці Голомбо, ми є здатні гарантувати оптимальне поширення навантаження для 6 пошкоджених комп'ютерів в інтервалі 26 = n = 30, тоді як ми можемо тільки гарантувати оптимальне поширення навантаження для 5 пошкоджених комп'ютерів для цього інтервалу, користуючись ощадливим підходом. Для інтервалу 31 = n = 34 ми можемо гарантувати оптимальне поширення навантаження аж до 6 пошкоджених комп'ютерів для обох схем відновлення заснованих на оптимальній послідовності Голомбо також як і для схеми відновлення, заснованіій на ощадній послідовності. На мал. 4 ми порівнюємо виконання схеми, користуючись лінійкою Голомбо з виконанням ощадливої схеми відновлення і виконанням схеми (org) відновлення як функції числа комп'ютерів. Виконання визначається як число вимкнень, якими ми можемо управляти, поки все ще є гарантія оптимального поширення навантаження. Мал. 4 показує, що схема поведінки лінійки Голомбо краща для великих значень n, наприклад, для n = 100, гарантії лінійки Голомбо оптимальна поведінка, навіть якщо 11 комп'ютерів Таб. 1 Порівняння оптимальної та ощадливої послідовносстей
вимикається, при ощадній схемі гарантува оптимальна поведінка, якщо 10 комп'ютерів вимикається а стара версія може тільки гарантувати оптимальну поведінку, доки вимкнені 6 комп'ютери. Для n = 1000, який ми можемо гарантувати оптимальну поведінку аж до 34 пошкоджених комп'ютерів, користуючись лінійкою Голомбо, 26 пошкоджених комп'ютерів, користуючись ощадливою схемою, тоді як стара схема тільки гарантує оптимальну поведінку аж до 9 пошкоджених комп'ютерів. Для n = 373, який ми можемо гарантувати оптимальну поведінку для аж до 22 пошкоджених комп'ютерів, користуючись схемою лінійки Голомбо. Для більших n це не відомо чи відповідні лінійки Голомбо оптимальні або ні. Крива абсолютів представляє Досконалу Лінійку Голомбо, коли ніякі відстані не нехтуються (подивіться визначення Досконалої Лінійки Голомбо [4]). Ніяка схема не може передавати цю межу і ми не знаємо, як закривають, один може фактично прибути в цю верхню межу.
Висновок У багатьох кластерних і розподілених системах, проектувальник повинен забезпечити схему відновлення. Такі схеми визначають, як робоче навантаження треба перерозподілити, коли один або більше комп'ютерів вимикається. Мета − тримати навантаження, порівну як тільки це можливо, навіть, коли самі несприятливі комбінації комп'ютерів вимикаються, тобто ми хочемо оптимізувати поведінку найгіршого випадку. Ми розглядаємо n ідентичних комп'ютерів, які за нормальних умов виконують один процес. Усі процеси виконують ту ж кількість роботи. Схеми відновлення, що гарантують оптимальне поширення навантаження в найгіршому випадку, коли x комп'ютерів вимкнулися є так звана оптимальна схема відновлення для значення n і x. Вкладення в цій статті, показують, що задача виявлення оптимальних схем відновлення системи з n комп'ютерами відповідає математичній задачі виявлення щонайдовшої послідовності додатніх цілих чисел таких, що сума менша, ніж n і суми з усіх послідовностей унікальні, називається лінійкою Голомбо. Важко визначити чинник алгоритму, який знаходить щонайдовшу послідовність з цими властивостями. Ми заздалегідь отримали схеми відновлення, які оптимальні, коли x ≤ log2 n [8]. Проте, в цій статті ми визначили ощадливу схему відновлення, яка оптимальна коли значно більший ряд комп'ютерів вимикається, і ми представили нову схему відновлення, схему лінійки Голомбо, для якої оптимально навіть більше число пошкоджених комп'ютерів. Для великого n різниця в термінах числа пошкоджених комп'ютерів, для яких ми можемо гарантувати оптимальну роботу, може бути істотною. Для прикладу, для n = 1000 Голомбо схема лінійки гарантує оптимальну роботу для в чотири рази більшої кількості пошкоджених комп'ютерів порівняно із старою схемою, тобто 34 ошкоджених комп'ютерів проти 9 пошкоджених комп'ютерів. Порівняно з ощадливою схемою відновлення це складає тільки 1.3 рази краще (34 пошкоджених комп'ютерів проти 26 пошкоджених комп'ютерів). (мал. 4) Перевага з ощадливим алгоритмом, порівнянно з лінійкою Голомбо, є, що ми можемо легко вичислити послідовність з чіткими частковими сумами також для великого n, де не відомі Правила Голомбо. Лінійка Голомбо відома довжинами аж до 41912 (з 211 позначками) [17,18,19]. З них перші 373 (з 23 позначками), відомо, оптимальні.
Мал..4 Представлення відмінностей між системою Лінійки Голомбо, ощадливою системою відновлення та старою системою відновлення Наші схеми відновлення можуть бути негайно використані в комерційних кластерних системах, наприклад визначаючи список в Сонячному Кластері, користуючись scconf командою. Результати можуть також будти використані, коли ряд зовнішніх систем, наприклад телекомунікаційні центри, що переключають відправку даних різним вузлам в розподіленій системі (або кластері, де вузли мають iндивідуальні мережеві адреси). У такому разі, списки відновлень також здійснюються як альтернативні місця призначення в зовнішніх системах або в протоколі комунікації рівень, наприклад IP протокол [12]. Список літератури 1. Ahrens, G., Chandra, A., Kanthanathan, M., Cox, D., Evaluating HACMP/6000: A Clustering Solution for High Availability Distributed Systems, in Proceedings of the Workshop in Fault−Tolerant Parallel and Distributed Systems, IEEE, College Station, TX, USA, 12−14 Juni, 1994, pp. 2−9 2. Bloom, G. S., Golomb, S. W., Applications of Numbered, Undirected Graphs, Proceedings of the IEEE, Vol. 65, No. 4, April, 1977, pp. 562−571 3. Dimitromanolakis, A., Analysis of the Golomb Ruler and the Sidon Set Problems, and Determination of large, near−optimal Golomb Rulers, Department of Electronic and Computer Engineering Technical University of Crete, June, 2002 4. Dollas, A., Rankin, W. T., McCracken, D., A new Algorithm for Golomb Ruler Derivation and Proof of the 19 Marker Ruler, IEEE Transactions on Information Theory, Vol. 44, No. 1, January 1998, pp. 379−382 5. Gardner, M., Wheels, Life and Other Mathematical Amusements, W.H.Freeman and Co., New York, 1983, Chapter 15, pp.152−165 6. Golomb, S. W., Taylor, H., Cyclic Projective Planes, Perfect Circular Rulers, and Good Spanning Rulers, Sequences And Their Applications – SETA’01, Proceedings of Seta01, Bergen, Norway, May 2001, pp. 166−180 7. Hayes, B., Computing Science: Collective Wisdom, American Scientist, Vol. 98, No. 2, March−April, 1998, pp. 118−122 8. Lundberg, L., Svahnberg, C., Optimal Recovery Schemes for High−Availability Cluster and Distributed Computing, Journal of Parallel and Distributed Computing 61(11), 2001, pp. 1680−1691 9. Managing MC/ServiceGuard for HP−UX 11.0, http://docs.hp.com/hpux/ha/ index.html 10. Comparing MSCS to other products, http://www.microsoft.com/ntserver/Product− Info/Comparisons/comparisons/CompareMSCS.asp 11. Mullender, S., Distributed Systems (Second Edition), Addison−Wesley, 1993 12. Pfister, G. F., In Search of Clusters, Prentice−Hall, 1998 13. Soliday, S. W., Homaifar, A., Lebby, G. L., Genetic Algorithm Approach to the Search for Golomb Rulers, International Conference on Genetic Algorithms, Pittsburg, PA, USA, 1995, pp. 528−535 14. Sun Cluster 2.1 System Administration Guide, Sun Microsystems, 1998. 15. TruCluster, Systems Administration Guide, Digital Equipment Corporation, http:// www.unix.digital.com/faqs/publications/cluster_doc 16. Vogels, W., Dumitriu, D., Agrawal, A., Chia, T., and Guo, K., Scalability of the Microsoft Cluster Service, Department of Computer Science, Cornell University, http://www.cs.cornell.edu/rdc/mscs/nt98 17. http://www.cuug.ab.ca:8001/~millerl/g3−records.html 18. http://www.distributed.net/ogr/index.html 19. http://www.research.ibm.com/people/s/shearer/grtab.html
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-22; просмотров: 322; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.102.163 (0.011 с.) |


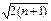 + 1/2.
+ 1/2. log2n, різниця між інтуїтивною схемою і оптимальною схемою може бути
log2n, різниця між інтуїтивною схемою і оптимальною схемою може бути  (тобто VL(x) = y) але навантаження на найбільш сильно занавантажееий комп'ютер в інтуїтивній схемі, можливо, таке високе, як
(тобто VL(x) = y) але навантаження на найбільш сильно занавантажееий комп'ютер в інтуїтивній схемі, можливо, таке високе, як  .
. .
.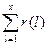 < n, потім R0(x) =
< n, потім R0(x) =  , (1 ≤ ≤ b ≤ x) є унікальний, тобто, коли
, (1 ≤ ≤ b ≤ x) є унікальний, тобто, коли  коли (1 ≤ a1 ≤ b1 ≤ x) і (1 ≤ a2 ≤ b2 ≤ x) і
коли (1 ≤ a1 ≤ b1 ≤ x) і (1 ≤ a2 ≤ b2 ≤ x) і  .
. . Це означає, що процес, який закінчується на комп'ютері y після i кроків був спочатку розподілений yf комп'ютер
. Це означає, що процес, який закінчується на комп'ютері y після i кроків був спочатку розподілений yf комп'ютер  ; і цей процес передав комп'ютер
; і цей процес передав комп'ютер 
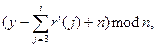 …,
…,  перед тим, як він досяг комп'ютера y. Списки нижче показують можливі послідовності комп'ютерів x яким необхідно вимкнутися для того, щоб головний процес закінчився на комп'ютері y, тобто, якщо комп'ютер (y−r'(1)+n) mod n − один додатковий процес закінчиться на комп'ютері y, комп'ютер (y−r'(1) − r'(2)+n)mod n і (y−r'(2)+n) mod n − інший додатковий процес закінчиться на комп'ютері y, і так далі.
перед тим, як він досяг комп'ютера y. Списки нижче показують можливі послідовності комп'ютерів x яким необхідно вимкнутися для того, щоб головний процес закінчився на комп'ютері y, тобто, якщо комп'ютер (y−r'(1)+n) mod n − один додатковий процес закінчиться на комп'ютері y, комп'ютер (y−r'(1) − r'(2)+n)mod n і (y−r'(2)+n) mod n − інший додатковий процес закінчиться на комп'ютері y, і так далі.



 ,(1 ≤ ≤ b ≤ x) унікальні. Це означає, що ніякий комп'ютер не включається в більш ніж один із списків. Отже, є ясно найгірший випадок, коли комп'ютери в найкоротших списках вимкнулися, наприклад для x = 3 найгірший випадок відбувається, коли комп'ютер:
,(1 ≤ ≤ b ≤ x) унікальні. Це означає, що ніякий комп'ютер не включається в більш ніж один із списків. Отже, є ясно найгірший випадок, коли комп'ютери в найкоротших списках вимкнулися, наприклад для x = 3 найгірший випадок відбувається, коли комп'ютер:  вимкнулися. Так само для x= 6 найгірший випадок відбувається, коли комп'ютер:
вимкнулися. Так само для x= 6 найгірший випадок відбувається, коли комп'ютер:  вимкнулися, а потім коли комп'ютери
вимкнулися, а потім коли комп'ютери  вимкнулися, а потім коли комп'ютери
вимкнулися, а потім коли комп'ютери  вимкнулися.
вимкнулися.





