
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Розділ 4. Диференціальне числення функції багатьох зміннихСодержание книги
Поиск на нашем сайте
Розділ 4. Диференціальне числення функції багатьох змінних Основні поняття У багатьох практичних задачах доводиться користатися величинами, що залежать не від однієї незалежної змінної, а від декількох змінних. Означення 4.1. Означення 4.2. Координатний простір називається
Означення 4.3. Нехай кожному числу Означення 4.4. Якщо кожній точці Той факт, що змінна
для явного завдання функції, і
для неявного завдання функції. Приклад 4.1. Знайти область визначення функцій: а) Розв’язання. Для випадку а) функція визначена для всіх значень Для випадку б) функція визначена при
Означення 4.5. Лінією рівня функції Рівняння лінії рівня має вигляд
Надаючи в цьому рівнянні різні значення сталої Для функції Для функції
Лінії рівня використовуються при складанні географічних карт (лінії рівня – лінії, в яких висота точок земної поверхні над рівнем моря однакова), при складанні метеорологічних карт (лінії рівня – ізобари, ізотерми, ізохори) і т.д.
Границя і неперервність
Для визначення границі функції введемо поняття околу точки Означення 4.6. Означення 4.7. Число Позначають Усі теореми про границі, доведені для функції однієї змінної поширюються і на функції багатьох змінних. Наприклад, Зауважимо, що слід розрізняти
Означення 4.8. Функція На випадок функції багатьох змінних переносять властивості неперервних функцій однієї змінної: сума, різниця, добуток неперервних у точці Аналогічно узагальнюється властивість неперервності складної функції. Функція При вивченні функції однієї змінної розглядалися основні властивості функцій, неперервних на відрізку. Ці властивості можна узагальнити на випадок функції багатьох змінних. До основних властивостей функції, неперервної в замкнутій обмеженій області 1. Функція обмежена в області 2. Функція досягає свого найменшого 3. Функція набуває хоча б в одній точці області
Частинні похідні функції Нехай у деякій області
який називається частинним приростом функції по змінній Означення 4.9. Частинною похідною по
Позначається частинна похідна по З означення частинних похідних випливає, що частинна похідна по будь-якій змінній є звичайною похідною цієї функції по обраній змінній, за умови, що інші змінні є сталими.
Тому обчислення частинних похідних не вимагає нових формул і правил диференціювання, крім тих, які відомі з диференціального числення функції однієї змінної. Наприклад, для функції
Повний диференціал Розглянемо неперервну функцію
Означення 4.10. Повним диференціалом функції двох змінних називається головна частина її приросту і позначається
Диференціал незалежної змінної дорівнює її приросту, тобто
Можна стверджувати, що
Цю формулу застосовують у наближених обчисленнях, заміняючи приріст функції її диференціалом. Приклад 4.2. Обчислити наближено Розв’язання. Для функції
Підставляючи значення, одержуємо
На підставі формули (4.6) у наближених обчисленнях оцінюють похибки обчислень. Приклад 4.3. При вимірі циліндра були отримані результати: Розв’язання. Об'єм циліндра обчислюється за формулою
Обчислюємо максимальну абсолютну похибку:
Відносну похибку результату,
Неявно задані функції Означення 4.14. Якщо змінна Наприклад, Розглянемо функцію
Продиференцюємо рівняння (4.10) по змінній
З останніх рівностей одержимо формули:
Аналогічно можна ввести поняття частинних похідних другого, третього, будь-якого порядку. Іноді неявні функції визначають системою функціональних рівнянь. Нехай функції
Розглянемо визначник:
Цей визначник називають визначником Якобі або якобіаном функцій Продиференцюємо рівняння системи (4.11) по змінній
Цю систему можна розв’язати відносно змінних
Умовний екстремум Розглянемо функцію
Нехай виконуються умови:
Дослідження функції (4.12) на екстремум при виконанні умов (4.13) називають задачею на умовний екстремум. Існує декілька шляхів розв’язання цієї задачі. Розглянемо метод Лагранжа. Побудуємо допоміжну функцію
де Приклад 4.7. Знайти умовний екстремум функції Розв’язання. Побудуємо функцію Лагранжа:
Дослідимо цю функцію на екстремум. Запишемо необхідну умову екстремуму та знайдемо стаціонарні точки з системи:
Стаціонарними точками будуть:
Для точки
Знак другого диференціалу невизначений, тобто в цій точці немає ні максимуму ні мінімуму. Для точки Оскільки
Метод найменших квадратів Часто при розв'язку практичних задач функціональна залежність між змінними задається у вигляді таблиці:
Для аналізу отриманого розв'язку зручно підібрати функцію, яка відповідала б таблиці експериментальних даних і якою можна було б скористатися для одержання значень функції. Зобразивши точки Так, якщо точки таблиці групуються біля деякої прямої, цю функцію можна шукати у вигляді лінійної функції Якщо ж точки розташовуються біля деякої параболи, то природно шукати функцію у вигляді квадратичної функції Якщо є вигляд функції, то залишається підібрати такі її коефіцієнти, при яких функція найкраще відповідала б таблиці. Підбор значень коефіцієнтів здійснюється методом найменших квадратів, що полягає в наступному: складають суму квадратів різниць значень функції в точках Нехай, наприклад, функція Ця функція з двома змінними
Перепишемо систему у вигляді
Система (4.14) є системою лінійних рівнянь відносно Приклад 4.9. Досліджуючи залежність врожайності від кількості внесених добрив (y – врожайність у ц/га, x – кількість добрив у ц/га) одержали такі дослідні дані:
Розв’язання. Побудуємо дослідну лінію залежності Як бачимо з рисунка, на проміжку Складемо для нашої задачі і розв’яжемо систему (4.14). Для цього скористаємося розрахунковою таблицею:
Знаходимо Система (4.14) набуває вигляду
Розв’язуючи систему, знайдемо, що Нехай тепер У цьому випадку сума квадратів відхилень значень функції: Функція
то система рівнянь для визначення коефіцієнтів набуває вигляду:
Перепишемо систему інакше:
Із системи (4.15) коефіцієнти
Економічні задачі Нехай задана виробнича функція Вираз Еластичність виробничої функції Якщо виробнича функція встановлює залежність випуску Приклад 4.10. Для випуску деякого товару визначена виробнича функція Розв’язання. Для визначення зміни виробничої функції за чинниками
За означенням еластичність функції за кожним з чинників така:
Обчислимо коефіцієнти еластичності при
Таким чином, зі збільшенням чинника При збільшенні чинника Відзначимо, що від'ємне значення коефіцієнта еластичності показує зменшення виробничої функції при збільшенні відповідного чинника. Наприклад, якщо Приклад 4.11. Фірма реалізує частину товару на внутрішньому ринку, а іншу частину поставляє на експорт. Зв'язок ціни товару Розв’язання. Сумарний доход:
В обох випадках ціна береться з відповідних кривих попиту.
Одержуваний фірмою прибуток
Знаходимо частинні похідні першого порядку:
Стаціонарна точка Обчислюємо частинні похідні другого порядку:
Виходить, у стаціонарній точці існує максимум. Знайдемо оптимальні ціни для продажу на внутрішньому і зовнішньому ринках, підставляючи координати точки максимуму в криві попиту:
Підраховуємо максимальний прибуток при оптимальних об'ємах продажу на внутрішньому і зовнішньому ринках:
Приклад 4.12. Фірма робить два види товарів
Потрібно знайти такі значення Розв’язання. Сумарний доход від продажу товарів
Прибуток
Це і є функція, максимум якої потрібно знайти. Для знаходження стаціонарних точок, визначаємо частинні похідні першого порядку від функції
Стаціонарна точка
Таким чином, точка
Вправи 4.1. Знайти область визначення функції і побудувати її на площині: а) 4.2. На площині а) 4.3–4.12. Знайти частинні похідні першого порядку. 4.3. 4.5. 4.7. 4.9. 4.11. 4.13. Знайти повні диференціали функцій: а) г) 4.14. Обчислити приблизно за допомогою повного диференціала: а) 4.15. Знайти похідну функцію 4.16. Знайти градієнт функції 4.17. Знайти напрямок найбільшої зміни функції 4.18. Знайти похідні другого порядку функцій: а) г) 4.19. Дослідити функції на екстремум: а) в) д) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| Поделиться: |

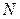 – вимірним координатним простором називається множина усіляких впорядкованих сукупностей
– вимірним координатним простором називається множина усіляких впорядкованих сукупностей 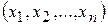 , де
, де  . Кожну таку сукупність будемо називати точкою
. Кожну таку сукупність будемо називати точкою  – вимірного координатного простору, тобто
– вимірного координатного простору, тобто  , де
, де  – координати точки
– координати точки  .
. , якщо між двома будь-якими точками
, якщо між двома будь-якими точками  та
та  визначена відстань:
визначена відстань: .
. ставиться в відповідність точка
ставиться в відповідність точка  , тоді ряд точок
, тоді ряд точок 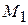 ,
,  ,...,
,..., 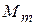 ,..., називається послідовністю точок
,..., називається послідовністю точок  .
. точок
точок 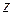 , то кажуть, що на множині
, то кажуть, що на множині  або
або 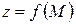 . При цьому множину
. При цьому множину 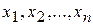 записують у вигляді
записують у вигляді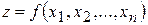 (4.1)
(4.1) (4.2)
(4.2) ; б)
; б)  .
.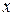 ,
, 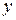 , при яких дріб
, при яких дріб  існує. Очевидно, що це ті
існує. Очевидно, що це ті  . Отже, область визначення даної функції зображується точками площини
. Отже, область визначення даної функції зображується точками площини  , що не належать прямій
, що не належать прямій  (рис.4.1).
(рис.4.1). або
або  . Графічно область визначення даної функції зображується точками круга (рис.4.2).
. Графічно область визначення даної функції зображується точками круга (рис.4.2).

 ,
,  . (4.3)
. (4.3)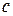 , будемо одержувати різні лінії рівня.
, будемо одержувати різні лінії рівня. лініями рівня є концентричні кола
лініями рівня є концентричні кола  ,
,  (рис.4.3). При
(рис.4.3). При  коло вироджується в точку.
коло вироджується в точку.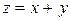 лініями рівня будуть прямі
лініями рівня будуть прямі  ,
,  (рис.4.4).
(рис.4.4).

 .
.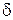 –околом точки
–околом точки 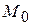 на відстань, що менше числа
на відстань, що менше числа 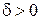 , тобто
, тобто  .
.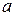 називається границею функції
називається границею функції  , якщо для кожного, як завгодно малого, наперед заданого додатного числа
, якщо для кожного, як завгодно малого, наперед заданого додатного числа  знайдеться такий
знайдеться такий  .
. або
або 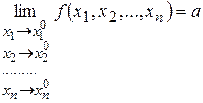 .
.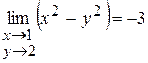 ,
,  .
.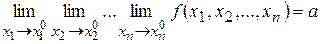 .
. , тобто значення неперервної функції в точці
, тобто значення неперервної функції в точці  двох неперервних у точці
двох неперервних у точці 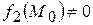 .
. , називається неперервною в цій області.
, називається неперервною в цій області. і найбільшого
і найбільшого 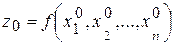 . Дамо аргументу
. Дамо аргументу 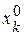 приріст
приріст  , не змінюючи інші змінні. Функція
, не змінюючи інші змінні. Функція  ,
, .
.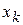 від функції
від функції  .
.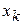 так:
так:  ,
,  ,
,  ,
,  .
. частинні похідні мають вигляд:
частинні похідні мають вигляд: ;
;  .
.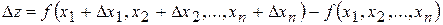 , або
, або
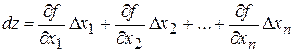 . (4.4)
. (4.4) . Тоді
. Тоді . (4.5)
. (4.5) . (4.6)
. (4.6) .
. ,
,  ,
,  ;
;  ;
;  ;
;  ;
;  . Тоді:
. Тоді: .
. .
. ,
,  . З якою абсолютною і відносною похибками може бути обчислений об'єм?
. З якою абсолютною і відносною похибками може бути обчислений об'єм?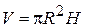 . За умовою задачі
. За умовою задачі  ,
,  . Отже, похибки змінних:
. Отже, похибки змінних:  ,
, 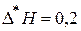 . Знайдемо частинні похідні
. Знайдемо частинні похідні  й
й  і їхні значення при
і їхні значення при  ,
,  :
: .
. .
. :
: .
.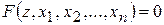 , то говорять, що функція задана неявно.
, то говорять, що функція задана неявно.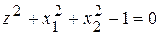 .
.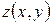 , задану рівнянням
, задану рівнянням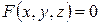 (4.10)
(4.10)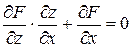 ,
, 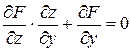
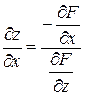 ,
, 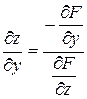 .
.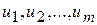 знаходять як розв’язки системи рівнянь:
знаходять як розв’язки системи рівнянь: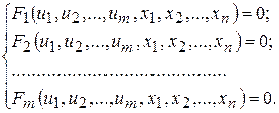 (4.11)
(4.11)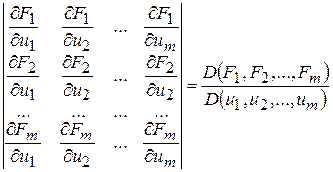 .
.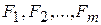 по змінним
по змінним 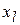 :
: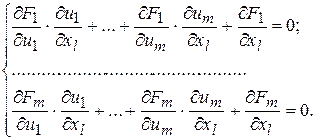
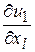 ,...,
,..., 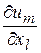 по формулам Крамера. Одержимо формули для знаходження частинних похідних:
по формулам Крамера. Одержимо формули для знаходження частинних похідних: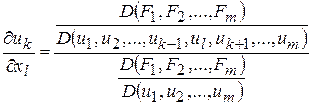 .
.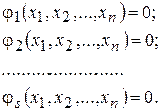 (4.13)
(4.13)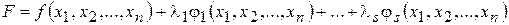 ,
,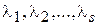 – поки що невідомі множники Лагранжа. Будемо досліджувати побудовану функцію на локальний екстремум.
– поки що невідомі множники Лагранжа. Будемо досліджувати побудовану функцію на локальний екстремум.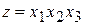 при умові:
при умові: 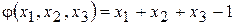 .
.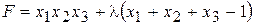 .
.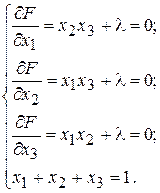
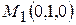 при
при 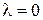 ,
, 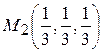 при
при 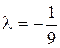 . Знайдемо другий диференціал в стаціонарних точках за формулою:
. Знайдемо другий диференціал в стаціонарних точках за формулою: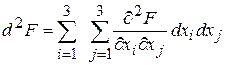 .
.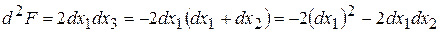 .
.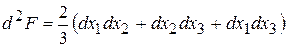 .
. , то
, то 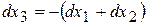 . Тоді одержимо:
. Тоді одержимо: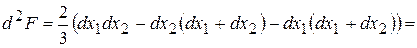
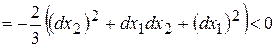 , тобто в цій точці максимум.
, тобто в цій точці максимум. на координатній площині, можна зробити висновок про вигляд функції
на координатній площині, можна зробити висновок про вигляд функції  .
.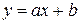 .
.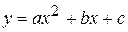 і т.д.
і т.д. , а потім підбирають коефіцієнти функції так, щоб ця сума була найменшою.
, а потім підбирають коефіцієнти функції так, щоб ця сума була найменшою. – лінійна, тобто
– лінійна, тобто  . Тоді
. Тоді 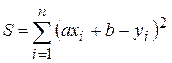 .
. набуває мінімуму в точках, для яких
набуває мінімуму в точках, для яких  і
і  , тобто
, тобто
 (4.14)
(4.14) Рис. 4.6.
Рис. 4.6.
 залежність
залежність  буде досить точно відображатися лінійною функцією
буде досить точно відображатися лінійною функцією 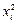
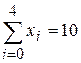 ,
,  ,
, 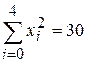 ,
,  .
. або
або 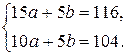
 ;
;  . Отже, залежність врожайності від кількості внесених добрив на 1 га найкраще відображає лінійна функція вигляду
. Отже, залежність врожайності від кількості внесених добрив на 1 га найкраще відображає лінійна функція вигляду  .
. є функцією трьох змінних
є функцією трьох змінних  досягає мінімуму в точках, для яких
досягає мінімуму в точках, для яких  . Оскільки
. Оскільки ,
,  ,
, ,
,
 (4.15)
(4.15) , що виражає залежність, наприклад, витрат виробництва від кількості двох видів продукції
, що виражає залежність, наприклад, витрат виробництва від кількості двох видів продукції  , тоді виробнича функція зміниться на
, тоді виробнича функція зміниться на 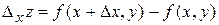 .
. відображає середній приріст виробничої функції на одиницю приросту чинника
відображає середній приріст виробничої функції на одиницю приросту чинника  , одержимо граничні витрати виробництва на одиницю продукції
, одержимо граничні витрати виробництва на одиницю продукції  . Аналогічно за чинником
. Аналогічно за чинником  .
. і вказує приблизно процентний приріст виробничої функції (підвищення, зниження), що відповідає приросту чинника
і вказує приблизно процентний приріст виробничої функції (підвищення, зниження), що відповідає приросту чинника 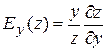 і вказує приблизно відсотковий приріст виробничої функції, що відповідає приросту чинника
і вказує приблизно відсотковий приріст виробничої функції, що відповідає приросту чинника  ,
,  ,...,
,...,  у вигляді
у вигляді  , то диференціальними характеристиками такої функції є:
, то диференціальними характеристиками такої функції є:  – гранична ефективність відносно чинника
– гранична ефективність відносно чинника  – еластичність випуску
– еластичність випуску  , де
, де  .
.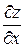 і
і  :
: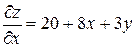 ;
;  .
. ;
;  .
.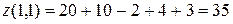 :
: ,
, 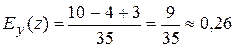 .
. і
і 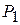 і його кількості
і його кількості  , проданого на внутрішньому ринку, описується рівнянням кривої попиту:
, проданого на внутрішньому ринку, описується рівнянням кривої попиту:  . Аналогічно для експорту ціна
. Аналогічно для експорту ціна  і кількість
і кількість  також зв'язані відношенням (рівнянням кривої попиту):
також зв'язані відношенням (рівнянням кривої попиту):  . Сумарні витрати визначаються виразом:
. Сумарні витрати визначаються виразом:  . Яку цінову політику повинна проводити фірма, щоб прибуток був максимальний?
. Яку цінову політику повинна проводити фірма, щоб прибуток був максимальний?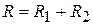 , де
, де  ,
,  – доходи від продажу на внутрішньому ринку і від експортних постачань відповідно:
– доходи від продажу на внутрішньому ринку і від експортних постачань відповідно: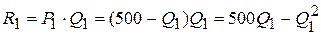 ,
, .
. .
.
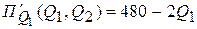 ,
,  ,
,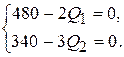
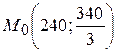 .
. ,
, 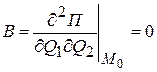 ,
, 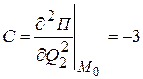 ,
,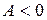 ,
, 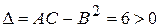 .
.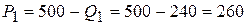 ,
, .
.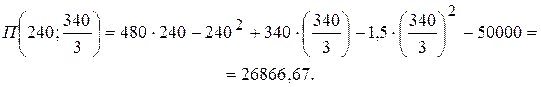
 і
і  і продає їх за ціною 1000 грош. од. і 800 грош. од. відповідно. Об'єми випуску товарів –
і продає їх за ціною 1000 грош. од. і 800 грош. од. відповідно. Об'єми випуску товарів –  .
. .
. являє собою різницю між доходом
являє собою різницю між доходом 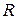 і витратами
і витратами  , тому
, тому  ,
, .
. і прирівнюємо їх до нуля:
і прирівнюємо їх до нуля: ,
,  ,
,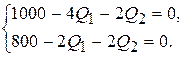
 . Знаходимо частинні похідні другого порядку:
. Знаходимо частинні похідні другого порядку: ,
,  ,
,  ,
,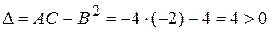 .
. ,
,  . Знайдемо суму максимального прибутку:
. Знайдемо суму максимального прибутку:
 ; б)
; б)  ; в)
; в) 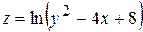 .
. ; б)
; б)  .
. . 4.4.
. 4.4.  .
. . 4.6.
. 4.6. 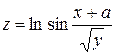 .
. . 4.8.
. 4.8. 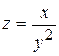 .
. . 4.10.
. 4.10.  .
.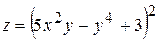 . 4.12.
. 4.12.  .
.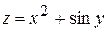 ; б)
; б)  ; в)
; в)  ;
; ; д)
; д)  .
. ; б)
; б)  ; в)
; в)  .
.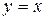 у точці
у точці  .
. в точці
в точці  .
. в точці
в точці  .
. ; б)
; б) 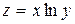 ; в)
; в)  ;
; ; д)
; д)  ; б)
; б)  ;
; ; г)
; г) 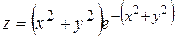 ;
;


