
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Локальний екстремум функції багатьох зміннихСодержание книги
Поиск на нашем сайте
Будемо говорити, що функція Сформулюємо необхідну умову екстремуму. Якщо функція Точки, в яких перші частинні похідні функції дорівнюють нулю чи не існують, називають критичними точками цієї функції. Екстремум функції може бути лише в критичних точках, тобто якщо функція не має критичних точок, то вона не має екстремуму. З існування критичних точок ще не випливає існування екстремумів, тобто необхідна умова екстремуму не є достатньою. Сформулюємо достатню умову екстремуму. Якщо другий диференціал в критичній точці являє собою додатньо визначену квадратичну форму, то в критичній точці локальний мінімум. Якщо квадратична форма від’ємно визначена, то в критичній точці локальний максимум. Якщо квадратична форма знакозмінна, то в критичній точці локального екстремуму немає. Зауважимо, що визначати вигляд квадратичної форми можна безпосередньо, а можна використовувати критерій Сильвестра. Нехай ми маємо квадратичну форму відносно змінних
Тоді в відповідності до критерію Сильвестра квадратичну форму вважають додатньо визначеною, якщо усі головні мінори матриці Розглянемо випадок функції двох змінних. Обчислимо значення змішаних похідних другого порядку функції Складемо вираз Якщо ж у критичній точці Приклад 4.6. Дослідити на екстремум функцію Розв’язання. Для даної функції Одержимо три критичні точки: Обчислимо другі частинні похідні функції: Для точки Достатня умова не дає відповіді на питання про існування екстремуму в точці
Для точки Аналогічно переконуємося в тому, що в точці
Неявно задані функції Означення 4.14. Якщо змінна Наприклад, Розглянемо функцію
Продиференцюємо рівняння (4.10) по змінній
З останніх рівностей одержимо формули:
Аналогічно можна ввести поняття частинних похідних другого, третього, будь-якого порядку. Іноді неявні функції визначають системою функціональних рівнянь. Нехай функції
Розглянемо визначник:
Цей визначник називають визначником Якобі або якобіаном функцій Продиференцюємо рівняння системи (4.11) по змінній
Цю систему можна розв’язати відносно змінних
Умовний екстремум Розглянемо функцію
Нехай виконуються умови:
Дослідження функції (4.12) на екстремум при виконанні умов (4.13) називають задачею на умовний екстремум. Існує декілька шляхів розв’язання цієї задачі. Розглянемо метод Лагранжа. Побудуємо допоміжну функцію
де Приклад 4.7. Знайти умовний екстремум функції Розв’язання. Побудуємо функцію Лагранжа:
Дослідимо цю функцію на екстремум. Запишемо необхідну умову екстремуму та знайдемо стаціонарні точки з системи:
Стаціонарними точками будуть:
Для точки
Знак другого диференціалу невизначений, тобто в цій точці немає ні максимуму ні мінімуму. Для точки Оскільки
|
||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 453; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.139.72.250 (0.009 с.) |

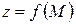 має в точці
має в точці 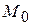 локальний максимум (мінімум), якщо знайдеться такий
локальний максимум (мінімум), якщо знайдеться такий 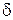 –окіл точки
–окіл точки 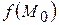 є найбільшим (найменшим) серед усіх значень
є найбільшим (найменшим) серед усіх значень  цієї функції. Максимум і мінімум функції називають екстремумами функції.
цієї функції. Максимум і мінімум функції називають екстремумами функції.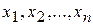 , тобто многочлен другого степеня відносно змінних
, тобто многочлен другого степеня відносно змінних  , яка визначена своєю матрицею:
, яка визначена своєю матрицею: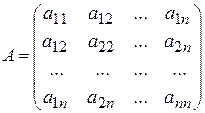 .
. додатні.
додатні. в критичній точці і позначимо
в критичній точці і позначимо 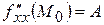 ,
, 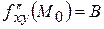 ,
, 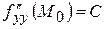 .
.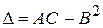 . Якщо в критичній точці
. Якщо в критичній точці 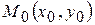 ,
, 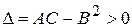 , то функція має екстремум у точці
, то функція має екстремум у точці 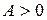 і максимум при
і максимум при 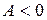 . Якщо в критичній точці
. Якщо в критичній точці 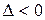 , то в точці екстремуму немає.
, то в точці екстремуму немає.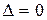 , то екстремум може бути, а може і не бути, потрібні додаткові дослідження.
, то екстремум може бути, а може і не бути, потрібні додаткові дослідження.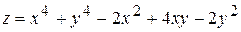 .
.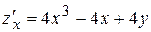 ,
, 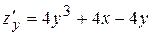 . Знайдемо критичні точки функції, розв’язавши систему рівнянь
. Знайдемо критичні точки функції, розв’язавши систему рівнянь 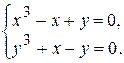
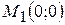 ,
, 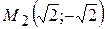 ,
, 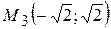 .
.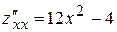 ,
, 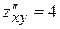 ,
, 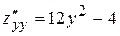 .
.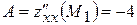 ,
, 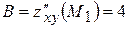 ,
, 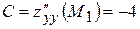 . Тоді
. Тоді 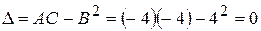 .
.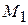 на прямій
на прямій 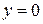 функція набуває вигляду
функція набуває вигляду 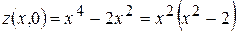 і є від'ємною. На прямій
і є від'ємною. На прямій 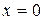 функція набуває вигляду
функція набуває вигляду 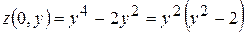 і також є від'ємною. На прямій
і також є від'ємною. На прямій 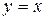 функція набуває вигляду
функція набуває вигляду 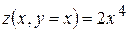 і є додатною. Отже, в околі точки
і є додатною. Отже, в околі точки 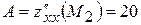 ,
, 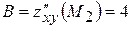 ,
, 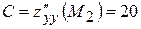 ,
, 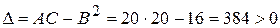 отже, екстремум є. Оскільки
отже, екстремум є. Оскільки 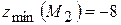 .
.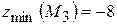 .
. , яка є функцією аргументів
, яка є функцією аргументів 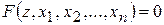 , то говорять, що функція задана неявно.
, то говорять, що функція задана неявно.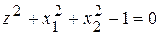 .
.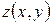 , задану рівнянням
, задану рівнянням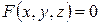 (4.10)
(4.10) та
та  :
: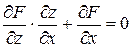 ,
, 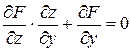
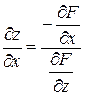 ,
, 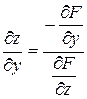 .
.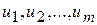 знаходять як розв’язки системи рівнянь:
знаходять як розв’язки системи рівнянь: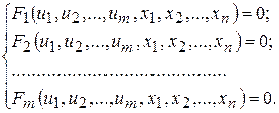 (4.11)
(4.11)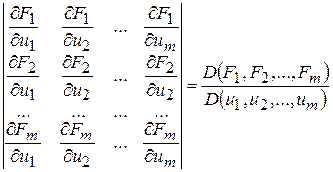 .
.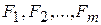 по змінним
по змінним 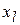 :
: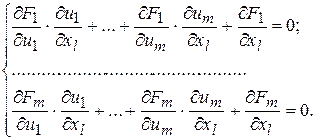
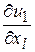 ,...,
,..., 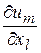 по формулам Крамера. Одержимо формули для знаходження частинних похідних:
по формулам Крамера. Одержимо формули для знаходження частинних похідних: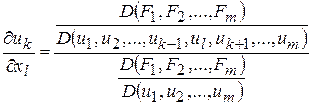 .
.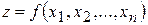 . (4.12)
. (4.12)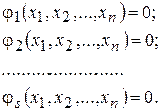 (4.13)
(4.13)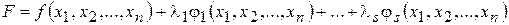 ,
,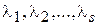 – поки що невідомі множники Лагранжа. Будемо досліджувати побудовану функцію на локальний екстремум.
– поки що невідомі множники Лагранжа. Будемо досліджувати побудовану функцію на локальний екстремум.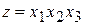 при умові:
при умові: 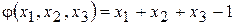 .
.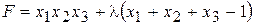 .
.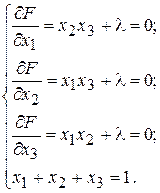
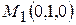 при
при 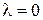 ,
, 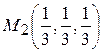 при
при 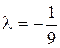 . Знайдемо другий диференціал в стаціонарних точках за формулою:
. Знайдемо другий диференціал в стаціонарних точках за формулою: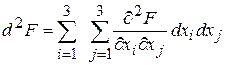 .
.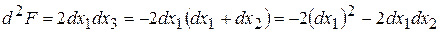 .
.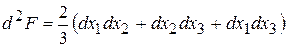 .
. , то
, то 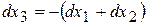 . Тоді одержимо:
. Тоді одержимо: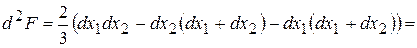
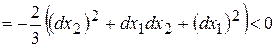 , тобто в цій точці максимум.
, тобто в цій точці максимум.


