
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Економічний зміст визначеного інтегралаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Нехай функція Зазначимо, якщо продуктивність праці не змінюється з часом ( Розіб'ємо відрізок
Тоді
Звідки
Отже, якщо
Властивості визначеного інтеграла Основні властивості визначених інтегралів наступні. 1) Значення визначеного інтеграла не залежить від позначення змінної інтегрування, тобто
Це твердження безпосередньо випливає з означення інтеграла як числа, рівного границі інтегральних сум. У випадку невід’ємної підінтегральної функції це особливо очевидно, тому що площа відповідної криволінійної трапеції не залежить від позначення осі абсцис. 2) Визначений інтеграл змінює знак при перестановці меж інтегрування, тобто
Нехай 3) Інтеграл від диференціалу змінної дорівнює: Дійсно, тут 4) Визначений інтеграл з однаковими межами інтегрування дорівнює нулю, тобто 5) Визначений інтеграл від алгебраїчної суми скінченного числа функцій дорівнює алгебраїчній сумі визначених інтегралів цих функцій, тобто
Справді, за означенням
6) Сталий множник можна виносити за знак визначеного інтеграла, тобто
Доведення цієї властивості аналогічне до доведення властивості 5. 7) Якщо відрізок
8) Якщо в кожній точці відрізка Справді, будь-яка інтегральна сума Наслідок. Якщо функція Якщо ж функція 9) Якщо в кожній точці відрізка
Дійсно, 10) Якщо функція
Справді, на підставі властивості 9:
Звідки Ця властивість може бути використана для оцінки величини визначеного інтеграла. Теорема про середнє значення інтегралу. Якщо функція
На підставі властивості 10 Отже,
Цікавий геометричний зміст цієї теореми. Якщо функція
Формула Ньютона–Лейбніца Нехай дано неперервну функцію Щоб не плутати змінну інтегрування з верхньою межею, далі будемо Доведемо, що функція
Знайдемо Бачимо, що неперервна функція
де Отже, функція, неперервна на відрізку Нехай
де Підставляючи в (5.31) значення
Підставляючи замість
Формула (5.32) називається формулою Ньютона–Лейбніца. Різницю
На підставі формули Ньютона–Лейбніца можна стверджувати, що визначений інтеграл дорівнює приросту первісної на відрізку. Це твердження часто зустрічається як означення визначеного інтеграла. Зазначимо, що при обчисленні визначеного інтеграла за формулою Ньютона–Лейбніца можна брати будь-яку первісну, тому що
Приклад 5.29. Обчислити інтеграл Розв’язання. Оскільки однією з первісних функцій
|
||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 508; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.136.73 (0.007 с.) |

 описує зміну продуктивності деякого виробництва з часом. Знайдемо обсяг продукції
описує зміну продуктивності деякого виробництва з часом. Знайдемо обсяг продукції  , виготовленої за проміжок часу
, виготовленої за проміжок часу  .
. – постійна функція), то обсяг продукції
– постійна функція), то обсяг продукції  , виготовлений за деякий проміжок часу
, виготовлений за деякий проміжок часу  , задається формулою
, задається формулою 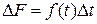 . У загальному випадку справедлива наближена рівність
. У загальному випадку справедлива наближена рівність  , де
, де  , що виявляється тим точнішою, чим менше значення
, що виявляється тим точнішою, чим менше значення 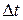 .
.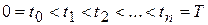 . Для обсягу продукції
. Для обсягу продукції  , виготовленої за проміжок часу
, виготовленої за проміжок часу  , маємо
, маємо , де
, де  ,
,  ,
,  .
. .
. .
.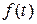 – продуктивність праці в момент часу
– продуктивність праці в момент часу  , то
, то  – обсяг продукції, що випускається, за проміжок
– обсяг продукції, що випускається, за проміжок 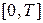 , а
, а  – обсяг продукції, що випускається, за проміжок
– обсяг продукції, що випускається, за проміжок  .
.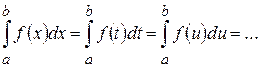 .
.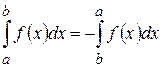 .
. . Тоді при складанні інтегральних сум, різниці
. Тоді при складанні інтегральних сум, різниці 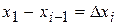 додатні для лівої частини рівності і від'ємні для правої частини рівності, що і пояснює властивість.
додатні для лівої частини рівності і від'ємні для правої частини рівності, що і пояснює властивість. .
. і
і 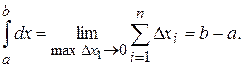
 .
.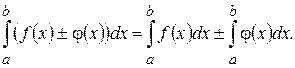


 розбитий точкою
розбитий точкою  на дві частини
на дві частини 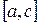 і
і  , то
, то .
. , то
, то  .
. для функції
для функції  на відрізку
на відрізку  і
і  . Отже,
. Отже,  .
.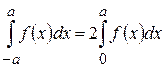 .
. .
. то
то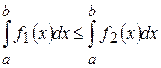 .
. , оскільки
, оскільки 
 – найменше значення функції,
– найменше значення функції,  – найбільше значення функції, тобто
– найбільше значення функції, тобто 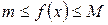 , то
, то .
.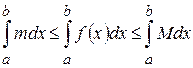 ;
; .
. .
.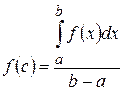 або
або . (5.29)
. (5.29) . Нехай
. Нехай  , тоді одержуємо
, тоді одержуємо 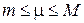 . За властивістю функцій, неперервних на відрізку знайдеться така точка
. За властивістю функцій, неперервних на відрізку знайдеться така точка 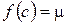 .
. .
. Рис. 5.2.
Рис. 5.2.
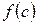 (рис. 5.2).
(рис. 5.2).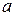 будемо вважати зафіксованою, а верхню границю
будемо вважати зафіксованою, а верхню границю 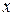 будемо вважати довільною, змінною. Тоді результат інтегрування буде залежати від
будемо вважати довільною, змінною. Тоді результат інтегрування буде залежати від  . Виходячи з геометричного змісту інтеграла
. Виходячи з геометричного змісту інтеграла  (рис. 5.3). Можна записати, що
(рис. 5.3). Можна записати, що  .
. , що справедливо на підставі властивості 1 визначеного інтеграла.
, що справедливо на підставі властивості 1 визначеного інтеграла. : похідна від інтеграла зі змінною верхньою межею за верхньою межею дорівнює значенню підінтегральної функції у верхній межі інтегрування.
: похідна від інтеграла зі змінною верхньою межею за верхньою межею дорівнює значенню підінтегральної функції у верхній межі інтегрування. Рис. 5.3.
Рис. 5.3.
 , де
, де  – площа криволінійної трапеції з основою
– площа криволінійної трапеції з основою  (рис. 5.3), тобто
(рис. 5.3), тобто 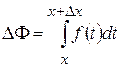 . Застосовуючи до останнього інтеграла теорему про середнє значення інтегралу, одержимо:
. Застосовуючи до останнього інтеграла теорему про середнє значення інтегралу, одержимо:  . Тоді
. Тоді  , що й було потрібно довести.
, що й було потрібно довести. , (5.30)
, (5.30)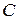 – довільна стала.
– довільна стала. – будь-яка первісна для функції
– будь-яка первісна для функції  , (5.31)
, (5.31) , одержуємо
, одержуємо 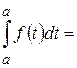
 або
або  . Звідки
. Звідки 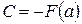 . Таким чином для всіх
. Таким чином для всіх  .
.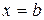 , одержуємо:
, одержуємо: . (5.32)
. (5.32)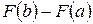 прийнято умовно записувати у вигляді:
прийнято умовно записувати у вигляді:  , тому, при обчисленні визначеного інтеграла запис оформлюють так:
, тому, при обчисленні визначеного інтеграла запис оформлюють так: .
. .
. .
. є функція
є функція 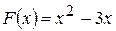 , то
, то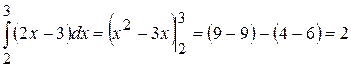 .
.


