
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Означення визначеного інтеграла. Геометричний і фізичний зміст визначеного інтеграла.Содержание книги
Поиск на нашем сайте
В попередньому пункті розглянуто дві задачі, взяті з різних галузей знання – одну з геометрії, іншу з фізики. Якщо абстрагуватися від конкретного змісту цих задач і зосередити увагу на їх аналітичній структурі, то бачимо, що в цьому сенсі вони цілком однакові. В обох випадках розв’язання задачі вимагає обчислення границі деякої суми цілком певної будови. Таку ж аналітичну структуру має величезна кількість задач, які виникають у різних галузях науки, техніки, економіки і взагалі людської діяльності. Виникає потреба у створенні спеціального математичного апарату для розв’язання подібних задач. Таким апаратом є визначений інтеграл. Означення. Нехай на відрізку
На кожному відрізку Якщо існує скінченна границя інтегральної суми при
Тоді функція Повертаючись до задач попереднього пункту, доходимо висновку, що а) площа б) шлях Зауважимо, що визначений інтеграл є числом, яке не залежить від позначення змінної інтегрування, тобто Виникає питання про умови, при яких визначений інтеграл існує. Теорема (достатня умова існування визначеного інтеграла). Якщо функція Ця умова є лише достатньою, тобто інтегровними можуть бути і деякі функції з точками розриву на проміжку інтегрування, але ми в подальшому вважатимемо підінтегральні функції неперервними, якщо не обумовлено протилежне.
|
||||
|
Последнее изменение этой страницы: 2016-12-28; просмотров: 228; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.26.135 (0.008 с.) |

 задана обмежена функція
задана обмежена функція 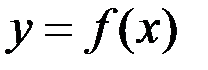 . Розіб’ємо відрізок
. Розіб’ємо відрізок  на
на  частинних відрізків точками
частинних відрізків точками .
. розбиття візьмемо довільно точку
розбиття візьмемо довільно точку  і позначимо
і позначимо  , де
, де  . Побудуємо суму
. Побудуємо суму  , яку будемо називати інтегральною сумою для функції
, яку будемо називати інтегральною сумою для функції  на відрізку
на відрізку  . Очевидно, що інтегральна сума залежить від способу розбиття відрізка
. Очевидно, що інтегральна сума залежить від способу розбиття відрізка  і від вибору проміжних точок
і від вибору проміжних точок 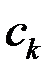 .
. (тобто при необмеженому подрібненні розбиття відрізка
(тобто при необмеженому подрібненні розбиття відрізка 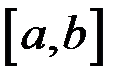 ) і ця границя не залежить ні від способу розбиття, ні від вибору проміжних точок
) і ця границя не залежить ні від способу розбиття, ні від вибору проміжних точок 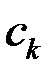 , то ця границя називається визначеним інтегралом функції
, то ця границя називається визначеним інтегралом функції  на відрізку
на відрізку 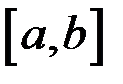 і позначається
і позначається .
. називається інтегровною на відрізку
називається інтегровною на відрізку  , числа
, числа  і
і  називаються відповідно нижньою і верхньою межами інтегрування, відрізок
називаються відповідно нижньою і верхньою межами інтегрування, відрізок  - проміжком інтегрування.
- проміжком інтегрування.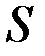 криволінійної трапеції, обмеженої прямими
криволінійної трапеції, обмеженої прямими  ,
, 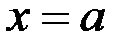 ,
,  і графіком функції
і графіком функції  , дорівнює визначеному інтегралу від цієї функції:
, дорівнює визначеному інтегралу від цієї функції:  (геометричний зміст визначеного інтеграла); якщо
(геометричний зміст визначеного інтеграла); якщо 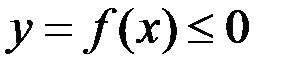 , то отримуємо відповідну площу із знаком мінус;
, то отримуємо відповідну площу із знаком мінус; , пройдений точкою за проміжок часу від
, пройдений точкою за проміжок часу від  до
до  , дорівнює визначеному інтегралу від швидкості
, дорівнює визначеному інтегралу від швидкості  :
:  (фізичний зміст визначеного інтеграла).
(фізичний зміст визначеного інтеграла). і т.д.
і т.д. неперервна на відрізку
неперервна на відрізку  , то вона інтегровна на цьому відрізку, тобто інтеграл
, то вона інтегровна на цьому відрізку, тобто інтеграл  існує.
існує.


