
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Задачі, що приводять до поняття визначеного інтеграла.Содержание книги
Поиск на нашем сайте
Задачі, що приводять до поняття визначеного інтеграла. 1) Задача про площу криволінійної трапеції.
Нехай на відрізку
 на будь-яке число на будь-яке число 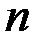 частин (відрізків) точками частин (відрізків) точками 
Довжину
Ці рівність тим точніша, чим дрібнішим є розбиття проміжку
Задача про шлях точки у прямолінійному русі. Нехай точка рухається по прямій з швидкістю Розіб’ємо проміжок часу від
Тривалість
Точність цієї формули збільшується із зменшенням усіх величин отже при необмеженому подрібненні розбиття, тобто при переході до границі при Приклади. 1) 2) Тут функція
3)
4)○
Обчислення визначеного інтеграла. Метод прямокутників
наблизимо не ступінчастою лінією, як у формулі прямокутників, а ламаною. Тоді площу криволінійної трапеції замінимо сумою площ відповідних прямокутних трапецій (рис. 5)
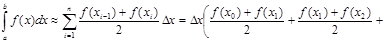   , ,
де Із зростанням числа n збільшується точність цієї формули. Метод парабол (формула Сімпсона)
Задачі, що приводять до поняття визначеного інтеграла. 1) Задача про площу криволінійної трапеції.
Нехай на відрізку
 на будь-яке число на будь-яке число 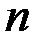 частин (відрізків) точками частин (відрізків) точками 
Довжину
Ці рівність тим точніша, чим дрібнішим є розбиття проміжку
|
|||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-28; просмотров: 221; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.12.165.168 (0.006 с.) |

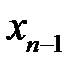


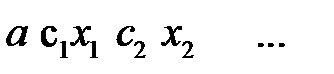



 задана невід’ємна обмежена функція
задана невід’ємна обмежена функція  . Потрібно знайти площу фігури, обмеженої графіком функції
. Потрібно знайти площу фігури, обмеженої графіком функції  , прямими
, прямими 
 і віссю абсцис
і віссю абсцис  (рис.1) Таку фігуру називають криволінійною трапецією.
(рис.1) Таку фігуру називають криволінійною трапецією. -ого частинного відрізка позначимо
-ого частинного відрізка позначимо 
 , на кожному частинному відрізку оберемо по одній точці
, на кожному частинному відрізку оберемо по одній точці 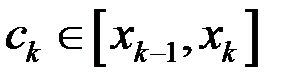 ,
,  . В точці
. В точці 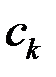 проведемо перпендикуляр до осі
проведемо перпендикуляр до осі  до зустрічі з кривою
до зустрічі з кривою  , через точку зустрічі проведемо пряму, паралельну осі
, через точку зустрічі проведемо пряму, паралельну осі  до зустрічі з прямими
до зустрічі з прямими  і
і  . Так на кожному частинному відрізку буде побудовано прямокутник з основою
. Так на кожному частинному відрізку буде побудовано прямокутник з основою  , висотою
, висотою  і, отже площею
і, отже площею  . Сукупність цих прямокутників утворює ступінчату фігуру, яка при достатньо дрібному розбитті буде як завгодно мало відрізнятися від заданої криволінійної трапеції. Тоді площа ступінчатої фігури, яка дорівнює сумі площ прямокутників, що її складають, наближено дорівнюватиме площі
. Сукупність цих прямокутників утворює ступінчату фігуру, яка при достатньо дрібному розбитті буде як завгодно мало відрізнятися від заданої криволінійної трапеції. Тоді площа ступінчатої фігури, яка дорівнює сумі площ прямокутників, що її складають, наближено дорівнюватиме площі  криволінійної трапеції:
криволінійної трапеції: .
. , і природно за площу криволінійної трапеції вважати границю площ ступінчатих фігур за умови необмеженого подрібнення розбиття, тобто при
, і природно за площу криволінійної трапеції вважати границю площ ступінчатих фігур за умови необмеженого подрібнення розбиття, тобто при  :
: .
. . Потрібно знайти шлях, пройдений точкою за проміжок часу
. Потрібно знайти шлях, пройдений точкою за проміжок часу  , тобто від моменту
, тобто від моменту  до моменту
до моменту  .
. до
до  на
на  частинних проміжків часу моментами
частинних проміжків часу моментами .
. -го часового проміжку позначимо
-го часового проміжку позначимо 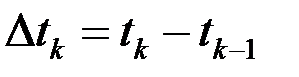 і в кожному такому проміжку оберемо по одному значенню
і в кожному такому проміжку оберемо по одному значенню 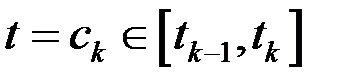
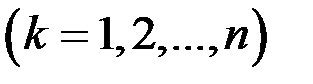 . Якщо розбиття проміжку
. Якщо розбиття проміжку  достатньо дрібне, то швидкість точки на
достатньо дрібне, то швидкість точки на  -ому частинному проміжку можна наближено вважати сталою, рівною
-ому частинному проміжку можна наближено вважати сталою, рівною 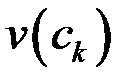 , а шлях, пройдений за цей проміжок часу, наближено рівним
, а шлях, пройдений за цей проміжок часу, наближено рівним  . Сума цих «частинних» шляхів дасть наближене значення всього шляху
. Сума цих «частинних» шляхів дасть наближене значення всього шляху  , пройденого точкою за проміжок часу
, пройденого точкою за проміжок часу  :
: .
. ,
, , отримуємо
, отримуємо  .
. .
. , де
, де  при
при  і
і  при
при  .
. має розрив у точці
має розрив у точці  , але на кожному з проміжків
, але на кожному з проміжків 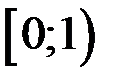 і
і  вона неперервна. Скористаємося з адитивності інтеграла:
вона неперервна. Скористаємося з адитивності інтеграла:

 .
. .
.
 точками
точками  на n рівних частин завдовжки
на n рівних частин завдовжки 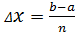 і на кожному відрізку
і на кожному відрізку  виберемо середню точку
виберемо середню точку 

 (i =1,2…n)
(i =1,2…n) ,
, Метод трапецій
Метод трапецій
 , (i =0,1…n).
, (i =0,1…n). та
та  і обмежена кривою y =
і обмежена кривою y =  ), то її площа дорівнює
), то її площа дорівнює  4
4  +
+  ), де y0, y2 – ординати крайніх точок, y1 – ордината кривої у середній точці. Такі параболи будуємо і для інших відрізків, сума їх площ дасть наближене значення інтеграла
), де y0, y2 – ординати крайніх точок, y1 – ордината кривої у середній точці. Такі параболи будуємо і для інших відрізків, сума їх площ дасть наближене значення інтеграла 
 +
+  +
+  .
. до інтегральної суми входять три значення функції.
до інтегральної суми входять три значення функції.


