
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основні властивості визначеного інтеграла.Содержание книги Поиск на нашем сайте
1) Визначений інтеграл з однаковими межами інтегрування дорівнює нулю: 2) Від переставлення меж інтегрування інтеграл змінює знак на протилежний Властивості 1) і 2) приймаються за означенням. Вони підказані процедурою означення інтеграла і виправдовуються далі способом обчислення інтеграла (формулою Ньютона-Лейбніца). 3) Cталий множник можна винести за знак визначеного інтеграла: 4) Визначений інтеграл від суми інтегровних функцій дорівнює сумі інтегралів від цих функцій: Ця властивість очевидним чином поширюється на випадок будь-якого скінченного числа доданків. Властивості 3) і 4) складають властивість лінійності визначеного інтеграла. 5) Якщо проміжок інтегрувння розбити на скінченну кількість частинних проміжків, то інтеграл по всьому проміжку дорівнює сумі інтегралів по частинних проміжках (властивість адитивності). Нехай функція Результат очевидним чином розповсюджується на випадок, коли проміжок 6) Нерівність можна почленно інтегрувати: якщо 7) Модуль визначеного інтеграла менший або рівний інтегралові від модуля підінтегральної функції: якщо функція 8) Інтеграл від одиничної функції дорівнює довжині проміжка інтегрування: 9) Якщо
Означення. Поділимо щойно одержану нерівність почленно на
Число 10) Якщо функція
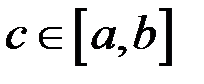 така, що така, що  . .
11) Інтеграли від парної і непарної функції в симетричних межах.
а) Якщо Графік непарної функції симетричний відносно початку координат (див. рис. 2). Тому площа Але
 парна функція парна функція  то то  . .
Графік парної функції симетричний відносно осі
Формула Ньютона-Лейбніца
Нехай функція Теорема. Якщо функція Отриману рівність називають формулою Ньютона-Лейбніца. Якщо ввести позначення
Формула Ньютона–Лейбница дає зручний спосіб обчислення визначе-ного інтеграла. Щоб обчислити визначений інтеграл від неперервної функції Приклади. 1) 2) Тут функція
3)
4)○
|
||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-28; просмотров: 455; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.53.93 (0.009 с.) |

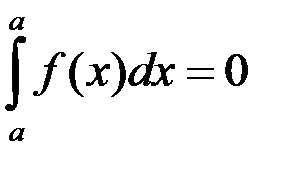
 .
.
 .
. .
. інтегрована на відрізку
інтегрована на відрізку  і
і  . Покажемо, що
. Покажемо, що  .
. розбивається на будь-яку скінченню кількість частинних проміжків. Зазначимо, що дана властивість стає цілком наочною, якщо розглянути її з точки зору геометричного тлумачення інтеграла.
розбивається на будь-яку скінченню кількість частинних проміжків. Зазначимо, що дана властивість стає цілком наочною, якщо розглянути її з точки зору геометричного тлумачення інтеграла. маємо
маємо  , то
, то 
 .
. інтегровна на відрізку
інтегровна на відрізку  то
то 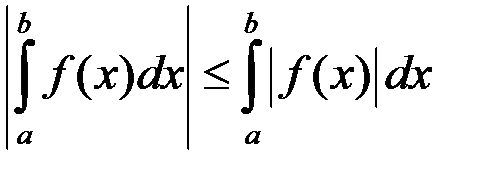
 .
.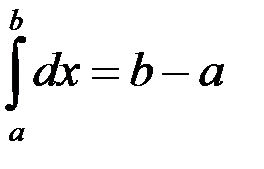 .
.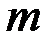 і
і  відповідно найменше і найбільше значення функції
відповідно найменше і найбільше значення функції  на відрізку
на відрізку 
 , то
, то (теорема про оцінку інтеграла).
(теорема про оцінку інтеграла). :
:
 називається середнім значенням функції
називається середнім значенням функції  на відрізку
на відрізку  . Оскільки
. Оскільки  , то
, то  є висота прямокутника, основною якого є відрізок
є висота прямокутника, основною якого є відрізок  , а площа дорівнює площі криволінійної трапеції, обмеженої прямими
, а площа дорівнює площі криволінійної трапеції, обмеженої прямими 
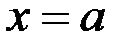 ,
,  і кривою
і кривою  .
. неперервна на відрізку
неперервна на відрізку  , то існує така точка
, то існує така точка  , що
, що 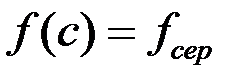 (теорема про середнє значення функції).
(теорема про середнє значення функції).








 непарна функція
непарна функція  , то
, то  .
. = площі
= площі  .
. -площа
-площа 
 на підставі властивості 5) і геометричного змісту інтеграла.
на підставі властивості 5) і геометричного змісту інтеграла.



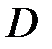



 , тому площа
, тому площа  = площі
= площі  (див. рис. 3)
(див. рис. 3) = 2 площі
= 2 площі  =
= 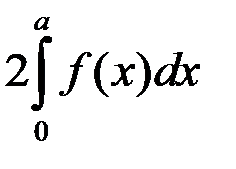
 інтегрована на відрізку
інтегрована на відрізку  .
. неперервна на відрізку
неперервна на відрізку  і
і  — яка-небудь її первісна, то має місце формула
— яка-небудь її первісна, то має місце формула  .
. , то формулу Ньютона-Лейбніца можна переписати так:
, то формулу Ньютона-Лейбніца можна переписати так: .
. на відрізку
на відрізку 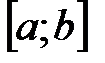 , треба знайти її первісну функцію
, треба знайти її первісну функцію 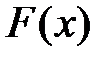 і узяти різницю
і узяти різницю  значень цієї первісної на кінцях відрізка
значень цієї первісної на кінцях відрізка  .
. .
. , де
, де  при
при  і
і  при
при  .
. має розрив у точці
має розрив у точці  , але на кожному з проміжків
, але на кожному з проміжків 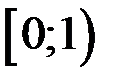 і
і  вона неперервна. Скористаємося з адитивності інтеграла:
вона неперервна. Скористаємося з адитивності інтеграла:

 .
. .
.


