
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Обчислення визначеного інтеграла.Содержание книги Поиск на нашем сайте
Інтегрування підстановкою (заміни змінної). Нехай для обчислення інтеграла Теорема. Якщо: 1) Функція 2) Множиною значень функції 3) то Доведення: Нехай Формула Відзначимо, що: 1) при обчисленні визначеного інтеграла методом підстановки повертатися до старої змінної не потрібно; 2) часто замість підстановки 3) не слід забувати міняти межі інтегрування при заміні змінних! Приклад. Обчислити ○ Покладемо Якщо Тому
Обчислення визначеного інтеграла. Інтегрування частинами. Теорема. Якщо функції Доведення: На відрізку Формула Приклад. Обчислити Розв’язання: Покладемо
Приклад. Обчислити інтеграл Розв’язання: Інтегруємо по частинах. Покладемо Інтегрування парних і непарних функцій в симетричних межах. Нехай функція
Розіб'ємо відрізок інтегрування В першому інтегралі зробимо підстановку
(згідно з властивістю: «визначений інтеграл не залежить від позначення змінної інтегрування»). Повертаючись до рівності (2), отримаємо
Якщо Завдяки доведеній формулі можна, наприклад, відразу, не проводячи обчислень, сказати, що
Наближене обчислення визначених інтегралів Нехай треба знайти визначений інтеграл
Метод прямокутників
наблизимо не ступінчастою лінією, як у формулі прямокутників, а ламаною. Тоді площу криволінійної трапеції замінимо сумою площ відповідних прямокутних трапецій (рис. 5)
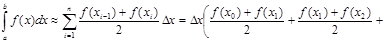   , ,
де Із зростанням числа n збільшується точність цієї формули. Метод парабол (формула Сімпсона)
|
||||||
|
Последнее изменение этой страницы: 2016-12-28; просмотров: 657; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.54.188 (0.009 с.) |

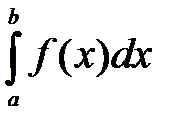 від неперервної функції зроблена підстановка
від неперервної функції зроблена підстановка 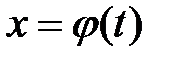 .
.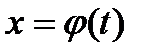 і її похідна
і її похідна 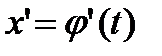 неперервні при
неперервні при  ;
; ;
;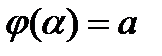 і
і 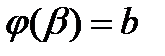 ,
, .
.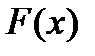 є первісною для
є первісною для  на відрізку
на відрізку 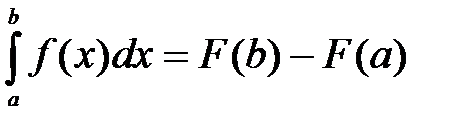 . Оскільки
. Оскільки  , то
, то  є первісною для функції
є первісною для функції 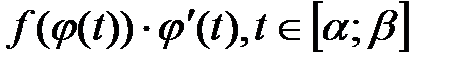 . Тому по формулі Ньютона-Лейбніца маємо
. Тому по формулі Ньютона-Лейбніца маємо  ■
■ ;
; .
. , тоді
, тоді  .
. , то
, то 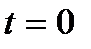 ; якщо
; якщо  , то
, то  .
.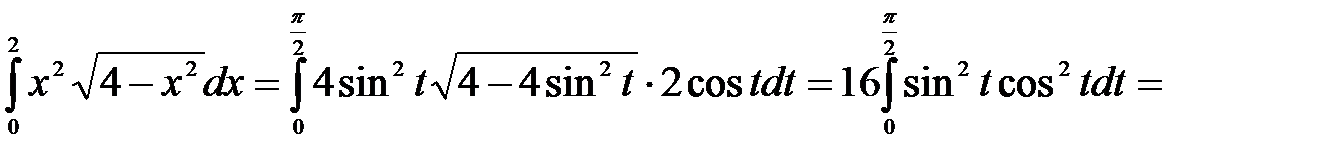
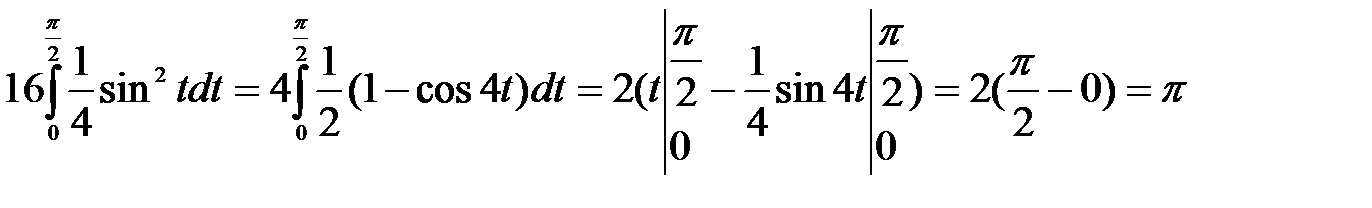 .●
.● і
і 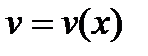 мають неперервні похідні на відрізку
мають неперервні похідні на відрізку 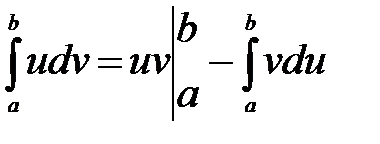 .
. . Отже, функція
. Отже, функція 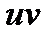 є первісною для неперервної функції
є первісною для неперервної функції  . Тоді по формулі Ньютона-Лейбніца маємо:
. Тоді по формулі Ньютона-Лейбніца маємо:  . Отже,
. Отже,  .■
.■ .
.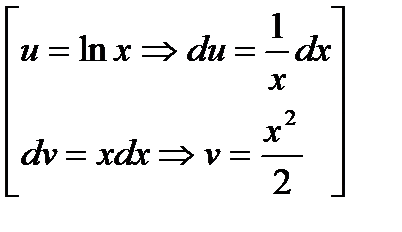 . Використовуючи формулу інтегрування по частинах, отримаємо
. Використовуючи формулу інтегрування по частинах, отримаємо
 . ○
. ○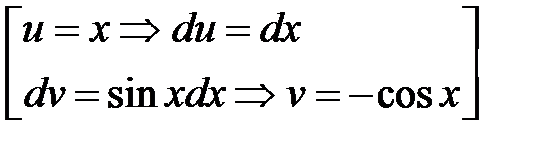 . Тому
. Тому  . ●
. ● неперервна на відрізку
неперервна на відрізку  , симетричному відносно точки
, симетричному відносно точки  . Доведемо, що
. Доведемо, що
 на частини
на частини 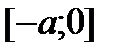 і
і 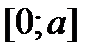 . Тоді за властивістю адитивності
. Тоді за властивістю адитивності  .
. . Тоді
. Тоді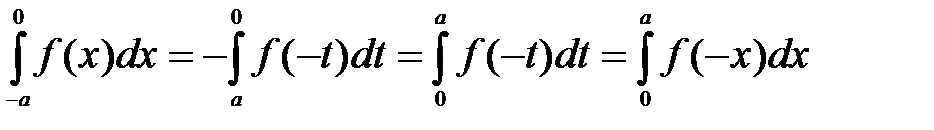
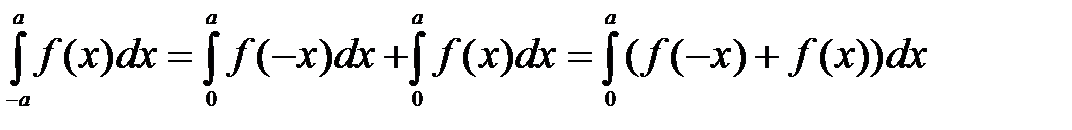 .
. парна ((
парна (( ), то
), то 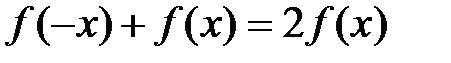 ; якщо функція непарна ((
; якщо функція непарна (( ), то
), то  .
. ,
,  .
. , де
, де  – деяка неперервна на
– деяка неперервна на 
 на n рівних частин завдовжки
на n рівних частин завдовжки 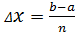 і на кожному відрізку
і на кожному відрізку  виберемо середню точку
виберемо середню точку 

 (i =1,2…n)
(i =1,2…n) ,
, Метод трапецій
Метод трапецій , (i =0,1…n).
, (i =0,1…n). та
та  і обмежена кривою y =
і обмежена кривою y =  ), то її площа дорівнює
), то її площа дорівнює  4
4  +
+  ), де y0, y2 – ординати крайніх точок, y1 – ордината кривої у середній точці. Такі параболи будуємо і для інших відрізків, сума їх площ дасть наближене значення інтеграла
), де y0, y2 – ординати крайніх точок, y1 – ордината кривої у середній точці. Такі параболи будуємо і для інших відрізків, сума їх площ дасть наближене значення інтеграла  +
+  +
+  .
. до інтегральної суми входять три значення функції.
до інтегральної суми входять три значення функції.


