
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основні властивості невизначеного інтегралаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Властивість 1. Знак диференціала перед знаком інтеграла знищує останній:
● Продиференціювавши рівність (1) дістанемо:
Властивість 2. Знак інтеграла перед знаком диференціала знищує останній, але при цьому вводиться довільний сталий доданок:
●Рівність (2) випливає з (1), якщо взяти Властивість 3. Сталий множник можна виносити за знак інтеграла:
●Справді, згідно з властивістю 1 диференціал лівої частини
подається так само, як і диференціал правої частини:
Якщо диференціали (4) і (5) обох частин рівності (3) однакові, то ці частини відрізняються лише сталою, яка вважається включеною в позначення невизначеного інтеграла. Властивість 4. Інтеграл алгебраїчної суми (різниці) функцій дорівнює сумі (різниці) інтегралів доданків:
Формула доводиться безпосередньою перевіркою диференціюванням. Справді, диференціал лівої частини подається так:
Найпростіші інтеграли. За формулами, якими подаються диференціали функцій, легко дістати відповідні формули інтегрування.
2. 3. 4. 5. 6. 7. Таблиця основних інтегралів 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. 19. 20. 21. 22. Література: В.П.Дубовик, І.І.Юрик „Вища математика”, К.,”АСК”,2001 Гл.7, стор. 330 – 336.
Тема 20 Означення та умови існування визначеного інтегралу. Властивості. Формула ньютона – Лейбніца
Мета заняття Узагальнити та систематизувати знання з теми. Розвивати уважність, вміння самостійно визначати головну думку, логічне мислення.
Студенти повинні знати: означення та умови існування визначеного інтеграла; властивості визначеного інтеграла, формулу Ньютона-Лейбница. Студенти повинні вміти: обчисляти визначені інтеграли; застосовувати властивості визначеного інтеграла для його обчислення.
Основні питання теми 1.Задачі, що приводять до визначеного інтеграла (про площу криволінійної трапеції, про роботу змінної сили, про пройдений шлях, про масу неоднорідного стержня); 2.Означення та умови існування визначеного інтеграла; 3.Властивості визначеного інтеграла; 4.Формула Ньютона – Лейбніца; 5.Геометричний зміст визначеного інтеграла; 6.Фізичний зміст визначеного інтеграла; 7.Необхідна та достатня умови інтегрованості; 8.Теорема про середнє значення функції; 9.Приклади.
Завдання для самоперевірки 1.Сформулювати теорему про існування визначеного інтеграла. 2.Сформулювати і довести властивості аддитивності і збереження знака визначеного інтеграла. 3.Із фігур, що обмежені лініями: а) в) д) виберіть ті, які не відповідають поняттю «криволінійна трапеція». 4. Визначеним інтегралом називається … 5. Геометричний зміст визначеного інтеграла полягає в тому, що … 6. Виберіть правильні твердження. Величина визначеного інтеграла залежить від: а) виду підінтегральної функції; б) позначення аргументу; в) проміжку інтегрування; г) області визначення первісної функції. 7.Теорема про середнє для визначеного інтеграла формулюється так … 8.Сформулюйте п’ять будь-яких властивостей визначеного інтеграла. 9. Які з формул: а) в) д) відбивають властивості визначеного інтеграла?
10.Обчислити інтеграли б) е) Література: В.П.Дубовик, І.І.Юрик „Вища математика”, К.,”АСК”,2001, стор.365 – 380.
Лекція „Визначений інтеграл” І. Поняття визначеного інтеграла. Означення. Скінченна границя І суми s при
де а, b — відповідно нижня та верхня межі інтегрування, ò — знак інтеграла, введений Лейбніцем. (Лейбніц увів знак інтеграла ò як витягнуту букву S, що позначає підсумовування.) У разі існування границі І функція f (x) називається інтегровною на проміжку [ a; b ].
Це відома формула Ньютона—Лейбніца, яка поєднує диференціальне числення з інтегральним. В інтегралі
Зауважимо, що означення визначеного інтеграла можна застосувати лише до обмеженої функції. Теорема. (Необхідна умова інтегрування.) Інтегровна на проміжку [ a; b ] функція обмежена.
|
||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 648; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.175.83 (0.006 с.) |

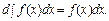

 (2)
(2)
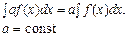 (3)
(3) (4)
(4) (5)
(5)















 1.
1. 
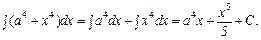








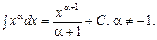



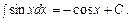






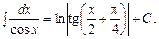
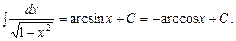


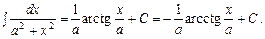





 б)
б) 
 г)
г) 

 б)
б) 
 г)
г) 

 в)
в) 

 називається інтегральною сумою, або сумою Рімана.
називається інтегральною сумою, або сумою Рімана. називається визначеним інтегралом від функції f (x) на відрізку [ a; b ] і позначається
називається визначеним інтегралом від функції f (x) на відрізку [ a; b ] і позначається (1)
(1) (2)
(2) символ х позначає змінну інтегрування. Цю змінну можна позначати будь-якою іншою буквою, а отже, завжди маємо:
символ х позначає змінну інтегрування. Цю змінну можна позначати будь-якою іншою буквою, а отже, завжди маємо:



