
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Похідна показникової функціїСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
¨ Диференціальне відношення (1) дорівнює
Згідно з наслідком 4 маємо:
Отже,
У частинному випадку при а = е дістаємо:
Похідна логарифмічної функції
¨ Записуємо диференціальне відношення (1):
Користуючись другою визначною границею, дістаємо
Отже, при
Зокрема, коли а = е, маємо:
Похідні тригонометричних функцій
¨ 1. Для функції у = sin x диференціальне відношення (1) подається так:
Згідно з першою визначною границею маємо:
Отже,
2. Аналогічно для функції у = cos x дістаємо:
3. Для функції у = tg х диференціальне відношення (1) набуває вигляду:
Згідно з наслідком 1 Отже,
4. Аналогічно для функції у = ctg x записуємо:
Правила диференціювання
¨
Рис. 3
¨
¨ Нехай у = u + v. Якщо D u і D v — прирости функцій u та v відносно приросту D х аргументу х, то приріст функції у такий:
Остаточно маємо:
·
¨ Нехай у = uv, де u і v — диференційовні функції від х; ∆ х — приріст аргументу х; D u і D v — прирости u і v. Тоді приріст функції у буде такий:
Рис. 4 Отже,
Коли D х прямує до нуля, маємо:
Тоді
Похідна добутку n функцій:
·
¨ Розглянемо точки, в яких виконуються умови: Нехай х набуває приросту D х; D у, D u, D v — відповідні прирости функцій у, u і v. Якщо
Віднімаючи від неї вираз
або
Якщо D х прямує до 0, маємо:
·
Похідна оберненої функції Теорема 1. Якщо функція у = f (x) монотонна й має в точці х відмінну від нуля похідну, то функція, обернена до даної, подається у вигляді х = g (y) і має похідну х = g (y), обернену до похідної даної функції:
Похідні обернених тригонометричних функцій:
¨ Якщо
За теоремою 1 маємо:
Похідна складної функції
Доведення. Позначимо u = j(х). Тоді у = f (u). Знайдемо прирости функцій у = f (u), u = j(x):
Далі запишемо диференціальне відношення (1):
Коли
Задана функція у = f (x). Знайти у ¢. 1) · 1) За формулою (5) маємо:
2) Візьмемо:
Функції
3) Нехай
Похідні функцій arctg x 3 і
Література: В.П.Дубовик, І.І.Юрик „Вища математика”, К.,”АСК”,2001, стор. 191 – 218.
Тема 13 Диференціал функції, його геометричний зміст. Властивості. Застосування диференціала в наближених обчисленнях Мета заняття Засвоєння поняття диференціалу функції в точці; формування уміння знаходити диференціали та застосовувати їх при наближених обчисленнях. Виховувати розумову культуру, культуру усного і писемного мовлення; розвивати логічне мислення.
Студенти повинні знати: поняття диференціалу функції, його геометричний зміст, властивості. Студенти повинні вміти: знаходити диференціал функції, застосовувати його в наближених обчисленнях.
Основні питання теми Ми знаємо, що процес знаходження похідних називається диференціюванням. Але в математичному аналізі є поняття диференціала функції в точці як самостійне. Що це таке і для чого, ви повинні вивчити в цій темі 1.Поняття диференціала функції в точці; позначення; 2.Властивості диференціала; 3.Геометричний зміст диференціала; 4.Застосування диференціала в наближених обчисленнях; 5.Приклади
Завдання для самоперевірки Закінчте вирази: 1. Похідною функції 2. Дотичною до графіка функції 3. Геометричний зміст похідної функції полягає в тому, що … 4. Фізичний зміст похідної функції полягає в тому, що … 5. Економічний зміст похідної функції полягає в тому, що … 6. Функція 7. Вказати правильне твердження: а) якщо функція б) якщо функція 8. Диференціалом функції 9. Геометричний зміст диференціала полягає в тому, що … 10. Якщо існують похідні функцій а) б) в) 11. Сформулювати і довести теорему про похідну складної функції. 12. Сформулювати і довести теорему про похідну оберненої функції. 13. Еластичністю функції називається … 14. Якщо існують еластичності а) б) 15. Попит називається еластичним, якщо … 16. Попит називається нееластичним, якщо … 17. Знайти відношення 1) 2) 3) 18. Використовуючи означення похідної як 1) 3) 5) 7) 19. Нехай витрати виробництва є функцією кількості випущеної продукції: 20. Обсяг виготовленої продукції у (ум. од.) цеху протягом робочого дня виражається такою функцією 21. У якій точці дотична до параболи 22. Знайти диференціал функції у = lnsin 2х: а)при довільних значеннях х і Δх; б)при х = π/8; в) при х = π/8 і Δх = 0,1. 23.Обчислити наближено arсtg 1,05. 24.Знайти диференціал функції у = lnsin 2х: а)при довільних значеннях х і Δх; б)при х = π/8; в) при х = π/8 і Δх = 0,1. 25.Обчислити наближено arсtg 1,05. Література: В.П.Дубовик, І.І.Юрик „Вища математика”, К.,”АСК”,2001, гл.5, стор. 218 – 222. Лекція „диференціал” Нехай функція у = f (x) диференційовна в інтервалі
Звідси можна записати:
де функція
Із (1) для приросту функції дістаємо:
Покладемо, що Означення. Величина f¢ (x)D х називається диференціалом функції f(x) за приростом Dх. Позначення: Геометрична інтерпретація: Диференціал
Рис. 1
Рис. 2 1)
2)
Правила обчислення диференціала Правило 1. Нехай Тоді або
Правило 2. Дано Тоді
Правило 3. Маємо Тоді
·
Правило 4. Якщо
Правило 5. Якщо функція
Правило 6. Якщо функції задані у параметричному вигляді
то
Інваріантність форми Важлива властивість диференціала функції полягає в тому, що його вигляд лишається незмінним навіть у тому разі, коли переходять до іншої незалежної змінної. ¨ Справді, нехай у = f (x). Тоді диференціал цієї функції записується у вигляді
Виконаємо заміну змінних u = j(x). Тоді функція у = f (u) буде функцією від змінної х:
Обчислюючи диференціал цієї функції, дістаємо:
або
Вираз
Отже, ми повернулися до вигляду диференціала (1), який був записаний за припущення, що змінна u є незалежною. Маємо властивість диференціала, яка називається його інваріантністю:
|
|||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 437; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.216.126.33 (0.008 с.) |


 .
. .
. .
. . ¨
. ¨

 .
. шукана похідна подається так:
шукана похідна подається так:
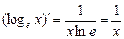 . ¨
. ¨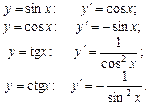
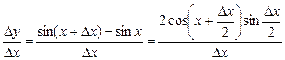 .
. .
.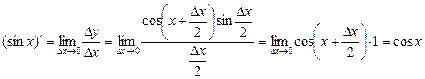 .
.
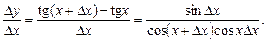
 .
. .
. ¨
¨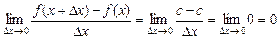 (рис. 3). ¨
(рис. 3). ¨
 (7)¢ = 0; (– 100)¢ = 0.
(7)¢ = 0; (– 100)¢ = 0.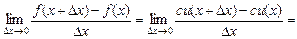

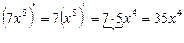 ·
· .
Аналогічно, похідна суми будь-якого скінченного числа диференційовних функцій дорівнює похідним цієї функції:
.
Аналогічно, похідна суми будь-якого скінченного числа диференційовних функцій дорівнює похідним цієї функції:
 .
.
 .
.
 ¨
¨ .
. .·
.· .
.

 (рис. 4).
(рис. 4).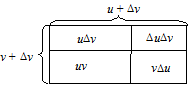
 .
. .
.


 ¨
¨ (3)
(3) .
. , відношення
, відношення  двох диференційовних функцій є функція диференційовна, причому
двох диференційовних функцій є функція диференційовна, причому
 .
.
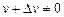 , коли D х близьке до нуля. Тоді виконується рівність
, коли D х близьке до нуля. Тоді виконується рівність .
. ,
, .
. . ¨
. ¨ .
.
 . ·
. · . (4)
. (4)
 , то для функцій
, то для функцій 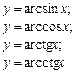 оберненими є відповідно такі:
оберненими є відповідно такі:
 ;
; ;
; ;
;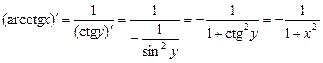 . ¨
. ¨ :
:
 —
правило ланцюга.
—
правило ланцюга.

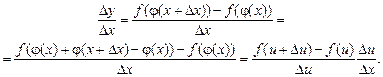
 то й
то й  . Тому
. Тому
 . ¨
. ¨ ; 2)
; 2)  ; 3)
; 3) 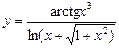 .
.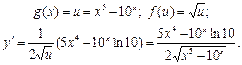
 . Тоді за правилом 4
. Тоді за правилом 4 .
.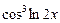 і
і  — складні. Згідно з (5) маємо:
— складні. Згідно з (5) маємо:
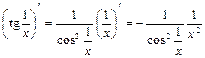 .
. і
і  . Тоді за правилом 5 дістаємо:
. Тоді за правилом 5 дістаємо: .
.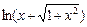 обчислюємо за формулою (5):
обчислюємо за формулою (5): ;
;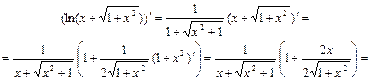
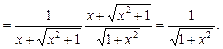
 у точці х називається
у точці х називається неперервна в точці х, то вона диференційовна в ній;
неперервна в точці х, то вона диференційовна в ній;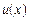 і
і  , то:
, то: … (довести);
… (довести);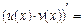 … (довести);
… (довести); … (довести).
… (довести).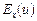 та
та  функцій
функцій  … (довести);
… (довести); … (довести).
… (довести). для функцій:
для функцій: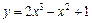 при
при 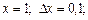
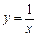 при
при 
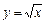 при
при  .
.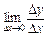 , знайти похідні функцій:
, знайти похідні функцій: ; 2)
; 2)  ;
;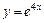 ; 4)
; 4) 
 ; 6)
; 6) 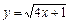 ;
; ; 8)
; 8) 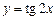 .
. . Знайти середні і граничні витрати виробництва за обсягу випущеної продукції, що дорівнює 10 грошовим одиницям.
. Знайти середні і граничні витрати виробництва за обсягу випущеної продукції, що дорівнює 10 грошовим одиницям.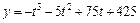 , де t — кількість годин роботи. Знайти обсяг випуску продукції через 2 години після початку робочого дня.
, де t — кількість годин роботи. Знайти обсяг випуску продукції через 2 години після початку робочого дня. : 1) паралельна осі ОХ; 2) утворює кут 45° з віссю ОХ?
: 1) паралельна осі ОХ; 2) утворює кут 45° з віссю ОХ? .
. 
 (1)
(1) при
при  задовольняє умову
задовольняє умову

 .
.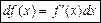
 є лінійним наближенням (апроксимацією) до приросту функції:
є лінійним наближенням (апроксимацією) до приросту функції:  . Наскільки менше
. Наскільки менше 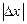 , настільки краще наближення (апроксимація) (рис. 1).
, настільки краще наближення (апроксимація) (рис. 1).
 . Знайдемо диференціал df (x) і приріст D f (x) для
. Знайдемо диференціал df (x) і приріст D f (x) для  і
і  і порівняємо їх.
і порівняємо їх.

 ;
;

 (рис. 2).
(рис. 2).

 .
.
 . ·
. · .
.
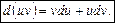
 .
.

 ,
, 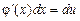 .
.

 . Знайти диференціал
. Знайти диференціал 
 за правилом 3 маємо:
за правилом 3 маємо: ·
· ,
,  , то
, то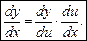
 , то
, то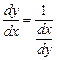 .
. ,
, 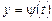 ,
, .
. Зауваження. Такі перетворення застосовують, виконуючи інтегрування функцій.
Зауваження. Такі перетворення застосовують, виконуючи інтегрування функцій. . (1)
. (1)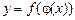 .
.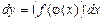 , (2)
, (2) . (3)
. (3)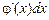 є диференціалом функції u, оскільки
є диференціалом функції u, оскільки  . Тому (3) можна подати у вигляді
. Тому (3) можна подати у вигляді .
.


