
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Похідна складної і неявної функціїСодержание книги Поиск на нашем сайте
Нехай Z=Z(u,v), a u=u(x,y), v=v(x,y). Для складної функції Z відносно змінних х і у необхідно знайти частинні похідні
Оскільки то
Зафіксуємо y (y=const). Тоді
або:
При
Аналогічно:
Якщо u=u(x), v=v(x), то з (6.1) дістанемо вираз для повної похідної:
Повний диференціал складної функції має вигляд:
= Отже,
Таким чином, встановлено інваріантність форми повного диференціала функції. Розглянемо неявні функції. Нехай маємо неявну функцію однієї змінної F(x,y)=0, для якої
Звідси:
Тепер розглянемо неявну функцію двох змінних F(x,y,z)=0. Тоді:
аналогічно,
Частинні похідні й диференціали вищих порядків Нехай z = f (x,y), тоді Якщо
або Останні дві похідні називають мішаними похідними другого порядку. Рівність мішаних похідних визначається теоремою: Теорема 7.1. Якщо функція z=f (x,y) та її похідні Диференціали вищих порядків
В §5 для функції двох змінних z=f (x,y) було встановлено формулу повного диференціала
або його ще називають диференціалом І-го порядку. За означенням диференціалом ІІ-го порядку називається диференціал від диференціала І-го порядку, тобто:
За формулою (7.1) маємо:
при цьому прийнято скорочено писати (dx)2=dx2, (dy)2=dy2. Аналогічно вводяться диференціали d3f, d4f і т.д. Для отримання виразів для диференціалів вищих порядків зручно скористатися таким підходом. Запишемо формально диференціал І-го порядку для функції z=f(x,y) у вигляді:
де вираз
називається оператором повного диференціала. За його допомогою вводиться оператор диференціала ІІ порядку:
Очевидно, що застосовуючи останній оператор до функції z=f(x,y), отримаємо формулу (7.2). Аналогічно, за допомогою оператора
можна записати диференціал ІІІ-го порядку
і т.д. Формула Тейлора для функцій одної і двох змінних
Нехай функція однієї змінної y=f(x) в околі точки х0 (n+1) -раз диференційована, тоді має місце Формула Тейлора:
де Rn(x) називається залишковим членом формули Тейлора. Для Rn(x) Лагранжем було встановлено, що
де С знаходиться в інтервалі (x0,x), якщо x0<x, або Користуючись формулами диференціалів, запишемо:
..........................................
Покладемо також
де Тоді формула Тейлора (8.1) прийме вигляд:
де Формулу (8.2) можна узагальнити для функцій двох змінних, якщо припустити, що функція z=f(x,y), або скорочено z=f(M), має в околі точки M0(x0 ,y0 ) (n+1) неперевну мішану частинну похідну по х і у. Тоді можна записати:
де Щоб записати формулу (8.3) в розгорнутому вигляді, необхідно скористатись формулами (7.1), (7.2), (7.3) і т.п.
|
|||||
|
Последнее изменение этой страницы: 2016-12-16; просмотров: 304; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.242.223 (0.01 с.) |

 і
і  . Нехай усі похідні існують.
. Нехай усі похідні існують. ,
, .
.
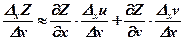 .
.
 (6.1)
(6.1) .
.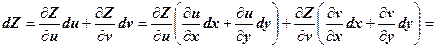

 .
. .
. .
.

 . Нехай y=const, тобто dy=0. Маємо:
. Нехай y=const, тобто dy=0. Маємо: , або:
, або:
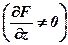 ,
,
 ,
,  .
. ,
,  можна диференцювати по х або у, то дістанемо похідні другого порядку:
можна диференцювати по х або у, то дістанемо похідні другого порядку: ,
,  ,
, ,
,  ,
, ,
, 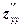 ,
,  ,
, 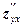 .
. ,
,  ,
, 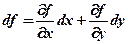 , (7.1)
, (7.1)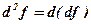 .
.
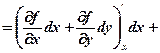
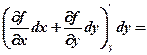
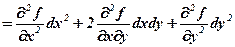 , (7.2)
, (7.2)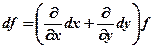 ,
, ,
, ,
, ,
,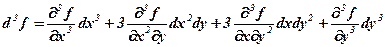 (7.3)
(7.3)
 , (8.1)
, (8.1)
 ,
,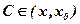 , якщо x<x0, скорочено
, якщо x<x0, скорочено  .
. ,
, ,
, ,
, ,
, .
. (8.2)
(8.2)
 , (8.3)
, (8.3) ,
,  ,
,  .
.


