
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Найбільше і найменше значення функції двох зміннихСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
В замкнутій області Нехай функція Приклад. Знайти найбільше значення добутку Розв'язання. Покажемо, що найбільше значення Знайдемо
Маємо функцію від незалежних змінних Геометрично - ця область є прямокутний трикутник, обмежений прямими Знайдемо похідні і прирівняємо до нуля:
Внутрі області розв'язком системи є Враховуючи, що на границі області Задача розв'язана, тому що при Умовний екстремум Локальний екстремум функції двох змінних без будь-яких додаткових умов називається безумовним. Якщо знаходиться екстремум функції за деяких додаткових умов, то він називається умовним. Нехай треба знайти екстремум функції
Рис.13.1.
Побудуємо допоміжну функцію трьох змінних, яка називається функцією Лагранжа: Необхідні умови екстремуму цієї функції мають вигляд:
Для встановления виду умовного екстремуму досліджують знак другого повного диференціала функції Лагранжа
в знайдених із системи (13.2) критичних точках при умові, що
Тоді функція Приклад 11.1. Знайти екстремум функції За методом Лагранжа: Запишемо необхідні умови екстремуму:
Звідки: Знайдемо другий диференциал функції Лагранжа. Оскільки
Отже, функція
Метод найменших квадратів При вивченні закономірностей в деяких дослідженнях інженерної справи, економіки, біології, медицини і т.п. приходиться аналітично описувати (у вигляді формули) зв'язок між двома змінними x та y. Для цього в процесі експериментів, спостережень вимірюють з можливою точністю окремі значення xi і відповідні їм значення yi (i=1,2,…,n), або отримують такі значення як статистичні дані. В результаті маємо таблицю значень (табл. 1).
Таблиця 1
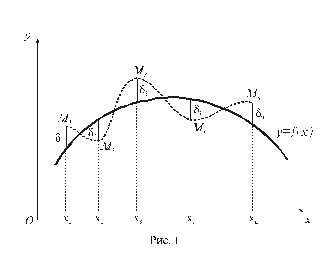
Подібну таблицю можна отримати, наприклад, при дослідженні лінійного розширення стержня в залежності від температури, якщо коефіцієнт лінійного розширення данного матеріалу невідомий, тоді x1, x2,…, xn – виміряні значення температури, а y1, y2,…,yn – відповідні їм значення довжини. Побудуємо у вибраній системі координат XOY точки Mi(xi, yi), координати яких відповідають даним таблиці 1 (див. рис. 1).
Тепер виникає необхідність вибору відповідної функції y=f(x), яка б описувала зв'язок між x і y. Таку функцію називають емпіричною. В загальному випадку вибір емпіричної функції не є однозначним. Можна знайти лінію, яка б проходила через кожну з точк Mi, це може бути так званий інтерполяційний многочлен (на рис. 1 це пунктирна лінія), порядок якого буде досить високим (на одиницю меншим, ніж кількість точок в таблиці). Крім того, дані таблиці 1 можуть бути не досить точними внаслідок наявності похибок вимірювання, а також впливу інших факторів, які ми не завжди можемо врахувати. Тому дослідники віддають перевагу більш простим і зручнішим функціям, таким, як лінійна
Позначимо через Параметри функції 10. Розглянемо випадок, коли
є функцією двох змінних a i b (xi, yi – це числа із таблиці 1). Відомо, що S (a,b) приймає мінімальне значення при тих значеннях a i b, при яких частинні похідні по цих змінних дорівнюють нулю, тобто коли
Із (14.1) знаходимо: Прирівнюючи до нуля частинні похідні, отримуємо систему рівнянь:
Система (14.2) називається нормальною системою методу найменших квадратів. Розв'язуючи систему рівнянь (14.2), знаходимо числа a i b, які підставляємо в рівняння Отже під "найкращим" згладжуванням експериментальних даних в даному випадку вважається лінійна функція, параметри якої знайдені за методом найменших квадратів. Метод найменших квадратів був запропонований німецьким математиком К. Гауссом. Приклад 1. З різних дільниць шахт у вигляді таблиці отримані середні дані за квартал про залежність між собівартістю 1 тони залізної руди (в грошових одиницях) і глибиною добування (розробки, в метрах) (табл.2). Таблиця 2
Припускаючи, що між змінними x i y існує лінійна залежність, знайти емпіричну формулу Розв'язання. Для зручності побудуємо обчислювальну таблицю (табл. 3). Таблиця 3
За значеннями сум таблиці складаємо нормальну систему методу найменших квадратів:
Зауважимо при цьому, що кількість точок в таблиці n=7. Систему розв'яжемо за формулами Крамера
Таким чином, емпірична формула залежності між глибиною розробки і собівартістю однієї тони залізної руди має такий вигляд:
Тепер згідно емпіричної формули обчислимо для відповідних значень xi теоретичні значення y(xi) і для порівняння заповнимо нову таблицю значень (табл. 4). Таблиця 4
Для більшої наочності побудуємо в системі координат XOY точки за даними таблиці 4 і пряму лінію
20. Зглажування квадратичною функцією
Знаходимо частинні похідні:
Прирівнюючи кожну з похідних до нуля отримуємо систему лінійних відносно a, b, c рівнянь:
Приклад 2. Застосовуючи метод найменших квадратів знайти значення параметрів функції
Таблиця 5
Розв’язання. Для наочності побудуємо точки за даними таблиці 5 в системі XOY (див. рис.3), розміщення яких нагадує параболу, для знаходження параметрів якої заповнюєм обчислювальну таблицю 6. Таблиця 6
Підставляючи значення сум із табл.6 в (14.3) отримуємо лінійну систему рівнянь відносно параметрів a, b, c:
Рис.3 30. Вирівнювання дослідних даних за гіперболою Таблиця 7
Після цього знаходиться мінімум функції
Для отримання системи (14.5) складається відповідна обчислювальна таблиця відносно значень необхідні для системи суми. Після знаходження 40. Вирівнювання дослідних даних за показниковою функцією
Приклад 3. За даними таблиці 8 знайти параметри залежності
Таблиця 8
Розв'язання. Побудуємо точки відповідно таблиці 8 (див. рис.4).
Рис.4
Складаємо обчислювальну таблицю Таблиця 9
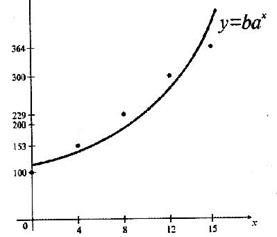
За даними сум таблиці 9 маємо систему:
для якої знаходимо визначники
Згідно формул Крамера знаходимо
Отже маємо лінійну функцію Поскільки
Вправи до розділу
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-16; просмотров: 612; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.14.29.19 (0.067 с.) |

 визначена і неперервна в обмеженій замкненій області D і має в ній скінчені частинні похідні. В цій області знайдеться точка
визначена і неперервна в обмеженій замкненій області D і має в ній скінчені частинні похідні. В цій області знайдеться точка  в якій функція приймає найбільше (найменше) значення.Якщо точка
в якій функція приймає найбільше (найменше) значення.Якщо точка  лежить усерединє області D, то в ній функція має максимум (мінімум), тому ця точка знаходиться серед критичних точок. Але найбільшого (найменшого) значення функція може досягати і на границі області. Тому, для того щоб знайти найбільше (найменше) значення функції
лежить усерединє області D, то в ній функція має максимум (мінімум), тому ця точка знаходиться серед критичних точок. Але найбільшого (найменшого) значення функція може досягати і на границі області. Тому, для того щоб знайти найбільше (найменше) значення функції 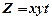 невід'ємних чисел
невід'ємних чисел 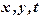 за умови, що їх сума є стала величина:
за умови, що їх сума є стала величина: 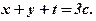
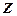 отримаємо при
отримаємо при 
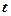 із даної умови:
із даної умови:  і підставимо в
і підставимо в 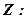
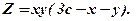
 в двовимірній області згідно умов:
в двовимірній області згідно умов: 
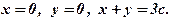
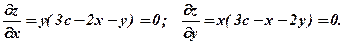
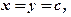 де
де 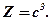
 то в знайденій точці
то в знайденій точці 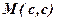 , дійсно функція має найбільше значення.
, дійсно функція має найбільше значення.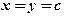 для змінної
для змінної 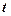 маємо
маємо 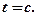 Згідно з результатом добуток невід'ємних чисел
Згідно з результатом добуток невід'ємних чисел  , сума яких дорівнює
, сума яких дорівнює 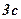 , не більше
, не більше 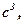 тобто
тобто 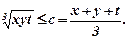 Отже середнє геометричне не більше середнього арифметичного. Це вірно для довільної кількості чисел.
Отже середнє геометричне не більше середнього арифметичного. Це вірно для довільної кількості чисел.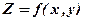 за умови
за умови 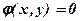 . Якщо вважати, що функція
. Якщо вважати, що функція  циліндр, то треба знайти екстремум не на всій поверхні, а тільки на лінії, яку вирізає з даної поверхні циліндрична поверхня (рис.13.1).
циліндр, то треба знайти екстремум не на всій поверхні, а тільки на лінії, яку вирізає з даної поверхні циліндрична поверхня (рис.13.1).
 (13.1)
(13.1) 
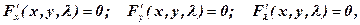 або:
або: (13.2)
(13.2)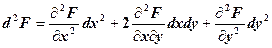
 і
і  зв’язані рівнянням
зв’язані рівнянням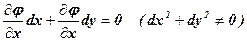 .
. має умовний максимум, якщо
має умовний максимум, якщо  , і функція
, і функція 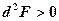 (див. 11.20)
(див. 11.20)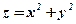 за умови
за умови 
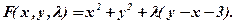


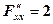 ,
,  ,
,  , то
, то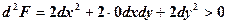 .
.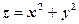 має умовний мінімум в точці
має умовний мінімум в точці  .
.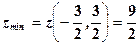 .
.
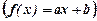 , квадратична
, квадратична  , показникова
, показникова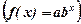 , гіперболічна
, гіперболічна  і ін. Вибрана функція повинна "найкращим" чином згладжувати експериментальні дані. В залежності від того, як вводиться поняття "найкраще згладжування" встановлюється той чи інший метод вибору емпіричної залежності
і ін. Вибрана функція повинна "найкращим" чином згладжувати експериментальні дані. В залежності від того, як вводиться поняття "найкраще згладжування" встановлюється той чи інший метод вибору емпіричної залежності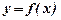 (на рис. 1 – суцільна лінія). Найбільш часто застосовується так званий метод найменших квадратів, який дозволяє знаходити параметри вибраної залежності
(на рис. 1 – суцільна лінія). Найбільш часто застосовується так званий метод найменших квадратів, який дозволяє знаходити параметри вибраної залежності 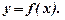
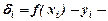 відхилення емпіричної функції в точці
відхилення емпіричної функції в точці 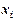 від відповідного табличного (експериментального) значення
від відповідного табличного (експериментального) значення 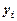 . Зрозуміло (див. рис. 1), що
. Зрозуміло (див. рис. 1), що  можуть бути для одних
можуть бути для одних 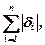 але досліджувати суму, яка містить модулі величин складніше, ніж суму квадратів цих величин. Тому зупиняються на останньому
але досліджувати суму, яка містить модулі величин складніше, ніж суму квадратів цих величин. Тому зупиняються на останньому 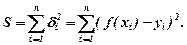
 вибирають так, щоб сума квадратів S приймала найменше значення.
вибирають так, щоб сума квадратів S приймала найменше значення.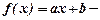 лінійна функція з невідомими параметрами a i b. Тоді величина відхилення
лінійна функція з невідомими параметрами a i b. Тоді величина відхилення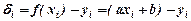 , а сума їх квадратів
, а сума їх квадратів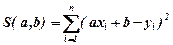 (14.1)
(14.1)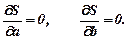
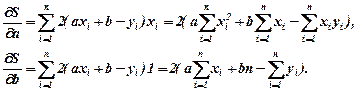
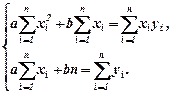 (14.2)
(14.2) що і дає формулу шуканої залежності.
що і дає формулу шуканої залежності.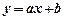 за методом найменших квадратів.
за методом найменших квадратів.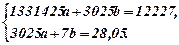
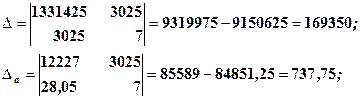


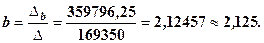
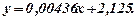 Із формули видно, що із збільшенням глибини розробки на 100 метрів собівартість 1 тони залізної руди в середньому зростає на
Із формули видно, що із збільшенням глибини розробки на 100 метрів собівартість 1 тони залізної руди в середньому зростає на 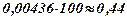 грошової одиниці.
грошової одиниці.
 експериментальних даних. Зауважимо, що метод найменших квадратів застосовується для знаходження параметрів після того, коли вигляд функції y=f(x) встановлений. Але якщо з теоретичних міркувань неможна зробити певного висновку, якою повинна бути емпірична формула, то її вигляд наочно визначають із графічних зображень експериментальних даних. Так із рис. 1 суцільна лінія, яка проходить поміж точок M1, M2, M3,…,Mi,…,Mn нагадує параболу
експериментальних даних. Зауважимо, що метод найменших квадратів застосовується для знаходження параметрів після того, коли вигляд функції y=f(x) встановлений. Але якщо з теоретичних міркувань неможна зробити певного висновку, якою повинна бути емпірична формула, то її вигляд наочно визначають із графічних зображень експериментальних даних. Так із рис. 1 суцільна лінія, яка проходить поміж точок M1, M2, M3,…,Mi,…,Mn нагадує параболу 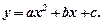 Тому у випадку квадратичної функції знаходимо мінімум суми
Тому у випадку квадратичної функції знаходимо мінімум суми  як функції трьох змінних a, b, c, при яких частинні похідні її повинні дорівнювати нулю
як функції трьох змінних a, b, c, при яких частинні похідні її повинні дорівнювати нулю
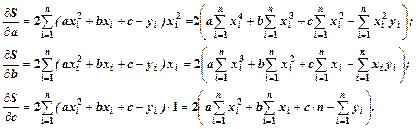
 (14.3)
(14.3) якщо відомі такі значення змінних (див. табл. 5).
якщо відомі такі значення змінних (див. табл. 5).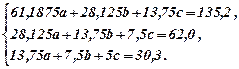 (14.4) Систему (14.4) можна розв'язати, наприклад, шляхом виключення невідомої
(14.4) Систему (14.4) можна розв'язати, наприклад, шляхом виключення невідомої  з наступним розв'язуванням нової системи відносно
з наступним розв'язуванням нової системи відносно  . Наводимо готові результати:
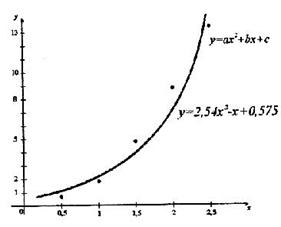
. Наводимо готові результати:  Шукана функція матиме вигляд:
Шукана функція матиме вигляд: 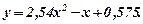
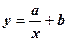 здійснюється за допомогою заміни
здійснюється за допомогою заміни 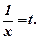 В такому разі в таблицю значень потрібно доповнити значеннями
В такому разі в таблицю значень потрібно доповнити значеннями 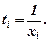
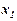
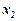
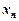

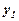



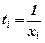

 яка має такий же вигляд, як функція (14.1), і тому відповідна система запишеться:
яка має такий же вигляд, як функція (14.1), і тому відповідна система запишеться: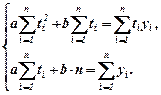 (14.5)
(14.5)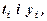 з якої знаходять
з якої знаходять
 здійснюється за допомогою логарифмування
здійснюється за допомогою логарифмування 
 і подальшою заміною
і подальшою заміною 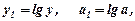
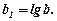 Тоді отримаємо лінійну залежність
Тоді отримаємо лінійну залежність 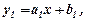 параметри якої
параметри якої  знаходимо за розглянутим вище методом найменших квадратів.
знаходимо за розглянутим вище методом найменших квадратів.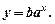
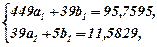
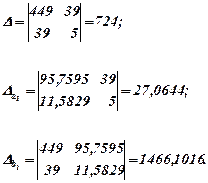
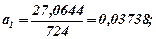

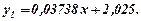
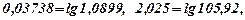 то
то 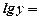
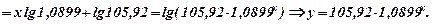 Таким чином, відповідно до таблиці 8 і рис. 4 ми знайшли показникову залежність
Таким чином, відповідно до таблиці 8 і рис. 4 ми знайшли показникову залежність 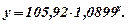
 при
при 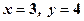 ;
;
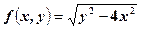 в точці
в точці  ;
;
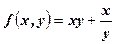 при
при 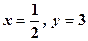 .
.
 .
.
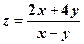 .
.
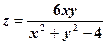 .
.
 .
.
 .
.
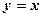 . 4. Уся площина за винятком кола
. 4. Уся площина за винятком кола  . 5. Круг радиуса 2 разом з його контуром. 6. кут між прямими
. 5. Круг радиуса 2 разом з його контуром. 6. кут між прямими  .
.
 .
.
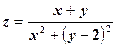 .
.
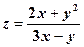 .
.
 .
.
 .
.
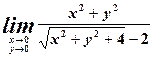 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
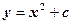 . 14. Сім’я концентрических кіл. 15. Сім’я рівнобічних гіпербол з асимптотами
. 14. Сім’я концентрических кіл. 15. Сім’я рівнобічних гіпербол з асимптотами 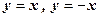 . 16. Сім’я паралельних прямих.
. 16. Сім’я паралельних прямих.
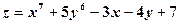 .
.
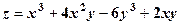 .
.
 .
.
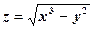 .
.
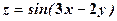 .
.
 .
.
 .
.
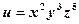 .
.
 .
.
 .
.
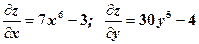 .
.
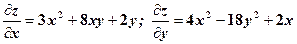 .
.
 .
.
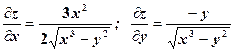 .
.
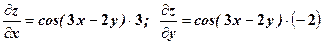 .
.
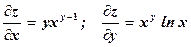 .
.
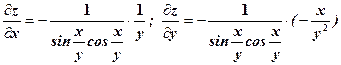 .
.
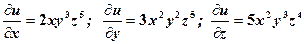 .
.
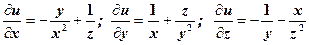 .
.
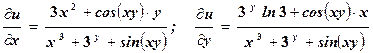
 , коли
, коли  .
.
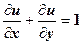 , коли
, коли 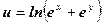 .
.
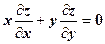 , коли
, коли 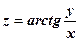 .
.
 .
.
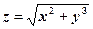 .
.
 .
.
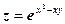 .
.
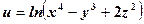 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 при
при 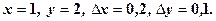
 при
при 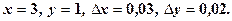
 при
при 
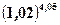 .
.

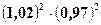
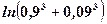
 та відносною
та відносною  похибками обчислено об’єм циліндра, якщо радіус основи
похибками обчислено об’єм циліндра, якщо радіус основи 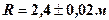 , а висота
, а висота 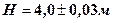 .
.

 Знайти
Знайти  .
.
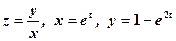 . Знайти
. Знайти 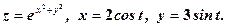 Знайти
Знайти 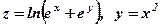 . Знайти
. Знайти 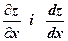 .
.
 Знайти
Знайти 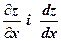 .
.
 Знайти
Знайти  .
.
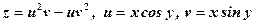 . Знайти
. Знайти 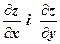 .
.
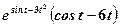 .
.
 .
.
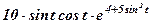
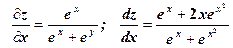
 .
.
 .
.
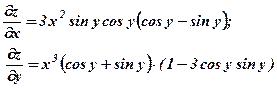
 . Знайти
. Знайти 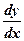 .
.
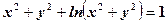 . Знайти
. Знайти  . Знайти
. Знайти 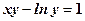 Знайти
Знайти 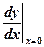 .
.
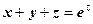 . Знайти
. Знайти 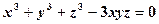 . Знайти
. Знайти 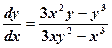 .
.
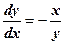 .
.
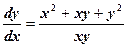 .
.
 .
.
 .
.
 .
.
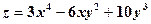 .
.
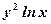 .
.
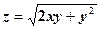 ,
, 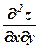 .
.
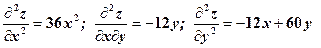 .
.
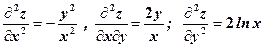 .
.
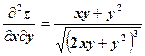 .
.
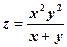 , то
, то 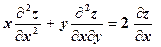 .
.
 , то
, то 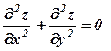 .
.
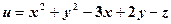 в точці
в точці 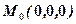 в напрямі відрізка
в напрямі відрізка 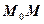 , де
, де 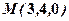 .
.
 в точці
в точці  в напрямі вектора
в напрямі вектора  .
.
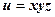 в точці
в точці 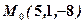 в напрямі від
в напрямі від 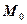 до
до 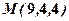 .
.
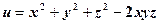 у точці
у точці  .В яких точках
.В яких точках  ?
?
 між градієнтами функцій
між градієнтами функцій 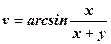 у точці
у точці 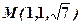 .
.
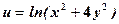 в точці
в точці  .
.
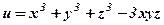 у точці
у точці 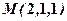 . Визначити, в яких точках він перпендикулярний до осі
. Визначити, в яких точках він перпендикулярний до осі 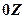 , та в яких дорівнює нулеві.
, та в яких дорівнює нулеві.
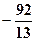 .
.
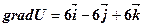 ,
, 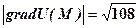 ;
; 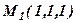 ,
, 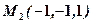 ,
, 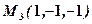 ,
, 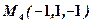 .
.
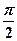 .
.
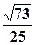 .
.
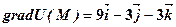 .
. 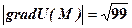 . У точках
. У точках 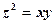 конуса – перпендикулярний
конуса – перпендикулярний 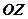 ; при
; при 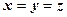 - дорівнює нулю.
- дорівнює нулю.
 .
.



