Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Функції кількох змінних. Область визначення.Содержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Лінії та поверхні рівня Означення 2.1. Змінна величина Z називається функцією двох змінних x і y, якщо кожній парі чисел (x, y) (або кожній точці М(x, y)) з деякої множини D площини xOy ставиться у відповідність визначене значення змінної Z. Позначається Z = f(x, y) або Z = f (M).
Наприклад. 1) Площа прямокутника S = xy є функцією двох змінних x і y – довжин відповідних сторін; 2) Об'єм конуса V = 1/3 p R2h – функція радіуса основи R і висоти h.
Означення 2.1. узагальнюється на більшу кількість змінних.
Означення 2.2. Змінна Z називається функцією незалежних змінних x1, x2 , … xn з деякої множини D, що належить n -вимірному простору Rn, якщо кожній точці М(x1, x2 , … xn) Z = f (M) = f (x1, x2 , … xn). Наприклад: 1) Температура Т в даній точці М залежить від її координат x, y, z, а також від моменту часу t, в який вона вимірюється, тобто T = f (x, y, z, t). 2) Очікуваний прибуток Р від споруджуваного промислового об'єкта є функцією затрат на його будівництво, часу t від початку будівництва до початку випуску продукції, від величини попиту Q на цю продукцію та інших економічних факторів.
Означення 2.3. Множина D точок, в яких функція визначена називається областю визначення або областю існування функції, а множина Е, яка складається із значень функції, називається множиною значень функції f (M). У випадку n = 2 функція двох змінних Z = f (x, y) може розглядатися як функція точки площини в тривимірному просторі R3. Графіком функції Z = f (x, y) є геометричне місце точок (x, y,) f (x, y)), яке описує деяку поверхню в просторі R3. Приклад 2.1. Знайти область визначення і множину значень функції
Рис 2.1
Приклад 2.2. Знайти область визначення поданих функцій: 1) 2) 3) 4) 1). Розв’язання для 1. Нагадаємо, що елементарна функція 2. Складаємо аналогічну нерівність для заданої функції двох змінних:
(1) 3. Замінимо останні нерівності рівняннями, отримаємо рівняння границі області визначення: х=2 – пряма, перпендикулярна осі ОХ, у=1 – пряма, перпендикулярна осі ОУ. Будуємо їх в системі ХОУ (див. рис. 2.2) 4. Відносно прямих х=2 і у=-1 вибираємо ті частини площини ХОУ, де виконуються нерівності (1) або (2).
Рис. 2.2.
2). Розв’язання для функції 1. Елементарна функція однієї змінної y=lg x визначена, якщо x>0. 2. Аналогічна нерівність для функції
3. Замінимо в (3) нерівність рівнянням: 4. Пробна точка О(0;0) задовольняє нерівність (3)
Отже, О(0;0) належить області розв’язків нерівності (3). Тобто вся область визначення – це множина точок, які лежать у середині заданого круга, виключаючи границю
Рис 2.3
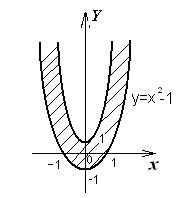
3) Розв’язання для функції 1. Відповідною елементарною функцією однієї змінної є 2. Аналогічна нерівність для функції
3. Замінивши нерівності на рівняння, отримаємо дві параболи 4. Пробна точка О(0,0) задовольняє ліву а також і праву нерівності (4)
Тобто початок координат знаходиться нижче першої параболи
Рис. 2.4 4) Розв’язання для функції 1. Відповідна функція однієї змінної 2. Для функції
3. Рівняння
півосі цього еліпса
4. Пробна точка О(0,0) нерівність (5) не задовольняє, бо нерівність
Рис 2.5
Приклади для самостійного розв’язання: Знайти область визначення функції: 1. 4. Відповіді. 1. Множина точок, які розміщені між віссю ОУ вище вітки параболи
3. Множина точок Означення 2.4. Лінією рівня функції Z = f (x, y) називається лінія f (x, y) = С на площині xOy, в точках якої функція має стале значення Z = C.
Означення 2.5. Поверхнею рівня функції U = f (x, y, z) називається поверхня f (x, y, z) = С, в точках якої функція має стале значення U = C. Приклад 2.3. Знайти лінії рівня функції
Рівняння ліній рівня (C > 0). Якщо С приймає дійсні значення, то отримуємо концентричні кола з центром в точці О(0,0), радіуса Зауважимо, що за допомогою ліній рівня f (x, y) = С можна побудувати поверхню Z = f (x, y) (рис. 2.2)
Рис. 2.6. Основними способами задання функції двох змінних є такі: 1) аналітичний, тобто за допомогою аналітичного виразу(формули); 2) табличний, за допомогою таблиці з двома входами, де кожній парі чисел
3) графічний, графіком функції двох змінних може бути деяка поверхня
|
||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-16; просмотров: 444; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.119.96 (0.012 с.) |

 D ставиться у відповідність визначене значення змінної Z:
D ставиться у відповідність визначене значення змінної Z: .
.

 Функція Z має дійсні значення за умови 1 – x2 – y2 ≥ 0, або x2 + y2 < 1, тобто областю визначення даної функції є замкнений круг радіуса 1 з центром в точці О(0,0). Множиною значень функції є сегмент [ 0, 1 ], що випливає з виразу Z = Ö 1 – x2 – y2. Графіком функції є верхня напівсфера радіуса 1 з центром в точці О(0,0,0).
Функція Z має дійсні значення за умови 1 – x2 – y2 ≥ 0, або x2 + y2 < 1, тобто областю визначення даної функції є замкнений круг радіуса 1 з центром в точці О(0,0). Множиною значень функції є сегмент [ 0, 1 ], що випливає з виразу Z = Ö 1 – x2 – y2. Графіком функції є верхня напівсфера радіуса 1 з центром в точці О(0,0,0).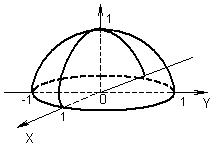
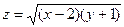 ;
;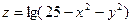 ;
; ;
; .
.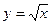 визначена, якщо
визначена, якщо  .
. , яка рівносильна двом системам нерівностей, а саме,
, яка рівносильна двом системам нерівностей, а саме,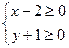 , або (2)
, або (2)  .
.
 . (3)
. (3)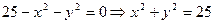 - коло радіуса 5 з центром в О(0;0), яке є границею області.
- коло радіуса 5 з центром в О(0;0), яке є границею області.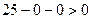
 , бо нерівність (3) строга (див. рис. 2.3).
, бо нерівність (3) строга (див. рис. 2.3).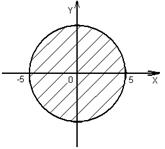
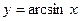 , яка існує для
, яка існує для 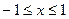 .
. . (4)
. (4) і
і  , які симетричні відносно осі ОУ з вітками напрямленими вверх, причому вершина першої з них в точці
, які симетричні відносно осі ОУ з вітками напрямленими вверх, причому вершина першої з них в точці 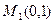 , а другої в точці
, а другої в точці  .
. ,
, 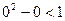
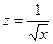 визначена для
визначена для  .
.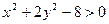 . (5)
. (5)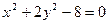 описує еліпс, канонічна форма якого:
описує еліпс, канонічна форма якого: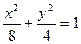 , (6)
, (6)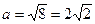 ,
,  .
. - невірна, тобто О(0,0), як внутрішня точка даної фігури, не входить у множину розв’язків нерівності (5). Множина розв’язків нерівності (5) – це всі точки, які лежать зовні еліпса. (див. рис. 2.4), не включаючи точок еліпса.
- невірна, тобто О(0,0), як внутрішня точка даної фігури, не входить у множину розв’язків нерівності (5). Множина розв’язків нерівності (5) – це всі точки, які лежать зовні еліпса. (див. рис. 2.4), не включаючи точок еліпса.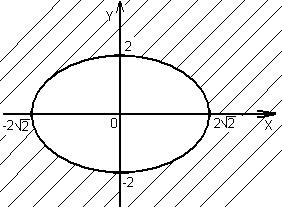

 2.
2. 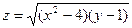 3.
3. 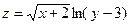
 5.
5. 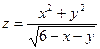 6.
6. 
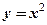 в першій чверті. 2. Множина точок
в першій чверті. 2. Множина точок  .
. . 4. Множина точок
. 4. Множина точок  , які розміщені на еліпсі
, які розміщені на еліпсі  та зовні його. 5. Множина точок
та зовні його. 5. Множина точок 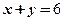 . 6. Областью визначення є смуга між двома паралельними прямими
. 6. Областью визначення є смуга між двома паралельними прямими 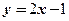 і
і  , включно з цими прямими.
, включно з цими прямими.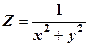
 мають вигляд
мають вигляд 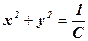
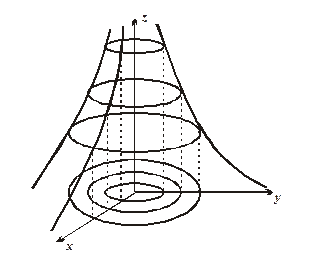
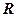 , де
, де  ..
..
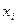 та
та 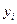 ставиться в таблиці відповідне значення
ставиться в таблиці відповідне значення