Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Картан, Анрі (нар. 1904) французький математикСодержание книги Поиск на нашем сайте
А математику ще й тому вивчати слід, що вона розум до ладу приводить. Ломоносов М.В. (1711-1765) –вчений-енциклопедист, поет Жодне технічне вдосконалення неможливе без складних розрахунків. Але так само важко уявити розвиток будь-якої науки, включаючи суспільні, без використання досягнень сучасної математики і кібернетики. Математика, все глибше проникаючи в суміжні з нею і віддалені науки, стає непохитною опорою прогресу людських знань. Митропольський Ю.О, (нар. 1917) – український математик У вивчення природи математика робить найбільший вклад, бо вона розкриває впорядкований зв’язок ідей, за яким побудований Всесвіт. Прокл (410-485)-грецький філософ Тим, хто не знає математики, важко збагнути справжню, глибоку красу природи Фейнман Р. (нар. 1918) – американський фізик
І.Функції багатьох змінних
Числові множини, способи їх задання. Побудова області на площині
Числова множина – це множина, елементами якої є числа. Відомо, що N, Z, Q, I, R – множини натуральних, цілих, раціональних, ірраціональних та дійсних чисел. Їх прийнято зображати у вигляді точок на числовій осі. Якщо елементами множини є впорядкована пара чисел, то маємо множину точок М(х,у) на площині ХОУ, така множина позначається R2. У випадку, коли елементами множини є впорядковані трійки чисел, то маємо множину точок М(x,y,z) у просторі, яка позначається R3. Часто доводиться розглядати впорядковані набори більшої кількості чисел. Наприклад, якщо х і у – координати точки місцевості, z – висота над рівнем моря в цій точці, t – температура, p – атмосферний тиск, g - відносна вологість повітря, v – величина швидкості вітру, a - напрям вітру, то впорядкований набір із восьми чисел (x, y, z, t, p,g, v, a) характеризує метеорологічний стан в даній місцевості. У загальному випадку впорядкований набір із n чисел (х1, х2, …, хn) по аналогії із n=2, n=3 теж зручно називати точкою, а множина точок М(х1, х2, …, хn) утворює n-вимірний арифметичний простірRn. Дві точки M1(x1',x2',…,xn') і M2(x1'',x2'',…,xn'') збігаються між собою, якщо x1'= x1", …, xn'= xn". Відомо, наприклад, що для двох точок М1(x1,y1,z1) і М2(x2,y2,z2) із простору R3 величина
є відстанню між цими точками. Подібним чином для двох точок М1 і М2, які належать Rn, величину
теж називають відстанню між точками М1 і М2. Окремі числові множини, як правило, задаються за допомогою нерівностей. Якщо всі нерівності строгі (<; >), то множина називається відкритою. Наприклад, інтервал: (a,b) = { x: a < x < b}; відкритий прямокутник: (a,b; c,d) = {(x,y): a<x<b, c<y<d}; відкритий паралелепіпед: (a,b; c,d; e,p) = {(x.y,z): a<x<b; c<y<d; e<z<p}. У загальному випадку можна говорити про відкритий n- вимірний паралелепіпед: (a1,b1; a2,b2; … an,bn ) = {(x1, x2, … xn): a1<x1<b1; a2<x2<b2; … an<xn<bn }. Cеред числових множин, які задаються нерівностями, часто зустрічаються також: (x-x0 )2 + (y-y0 )2 < r2 - відкритий круг у просторі R2 радіуса r з центром в точці М0 (x0 , y0 ); (x-x0 )2 + (y-y0 )2+ (z-z0 )2 < r2 - відкрита куля у просторі R3 радіуса r з центром в точці М0 (x0 , y0,z0 ); (x1-x10)2 + (x2-x20)2 + … + (xn-xn0)2 < r2 - відкрита куля в просторі Rn радіуса r з центром в точці М0 (x01 , х02, …, х0n ). Означення 1.1. Околом точки називається довільна відкрита множина, яка містить дану точку. У двовимірному випадку під околом точки
Означення 1.2. Множина точок називається зв'язною, якщо дві точки цієї множини можна з'єднати ламаною лінією, всі точки якої належать цій множині.
Означення 1.3. Точка М називається внутрішньою точкою множини D, якщо вона належить D разом з її достатньо малим околом.
Означення 1.4. Зв'язна множина, яка цілком складається із внутрішніх точок, називається областю. Означення 1.5. Граничною точкою області D називається точка, в будь-якому околі якої знаходяться точки, які як належать області D, так і не належать їй. Означення 1.6. Множина граничних точок області D називається її границею Г.
Означення 1.7. Область D разом з її границею Г називається замкненою областю D (позначається Посилаючись на геометричну інтуіцію, можна сказати, що якщо з геометричного тіла зідрати його границю, то отримаємо відкриту множину. На рисунку 1.1. точка М0 (x0 , y0 ) – внутрішня точка області D, точка М1 належить границі Г області D. Область D – відкрита, а область
Рис. 1.1.
На рисунку 1.1. окіл точки М0 (x0 , y0 ) зображений в вигляді круга і квадрата. Наприклад, замкнені області: сегмент: [a, b] = замкнений прямокутник: [a, b; с, d] = замкнений круг радіуса r з центром в точці М0 (x0, y0 ):
замкнений трикутник:
Таким чином, в замкнених областях обмеження задаються нестрогими нерівностями В подальшому для наочності будемо вивчати числову множину R2, тобто сукупність точок на площині. Для побудови області на площині треба знайти такі точки М(x,,y), координати яких задовольняли б нерівностям, які задають множину. Приклад 1.1. Побудувати область D на площині, яка задана нерівностями:
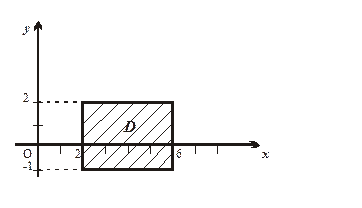
Даним нерівностям задовольняють координати точки, яка знаходиться всередині або на границі прямокутника, сторони якого лежать на прямих х = 2; х = 6; y = -1; y = 2. Цей прямокутник є замкненою областю (рис. 1.2)
Рис 1.2.
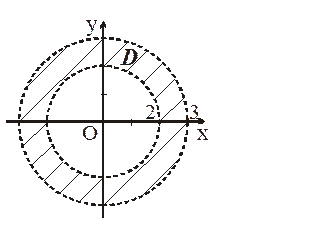
Приклад 1.2. Побудувати область D, яка задана нерівностями: 4 < x2 + y2 < 9. Даним нерівностям задовольняють координати точок, які знаходяться всередині кругового кільця, обмеженого колами x2 + y2 = 4 та x2 + y2 = 9 з центрами в точці О(0, 0) та радіусами r1 = 2, r2 = 3. Таким чином, це кругове кільце – відкрита область D (рис. 1.3).
Рис. 1.3.
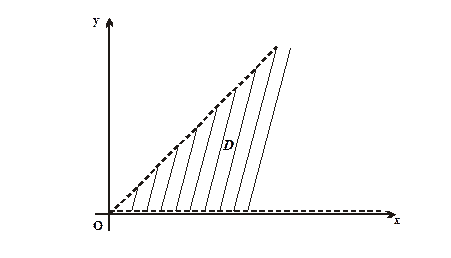
Приклад 1.3. Побудувати область D, задану нерівностями 0 < y < x В даному випадку маємо відкриту область D, яка обмежена прямими y = x та y = 0 (рис. 1.4.). Геометрично – це всі точки, що знаходяться внутрі кута. Точки, що розміщені на сторонах кута області D не належать, тому на рис.1.4 сторони кута зображені пунктиром. Розглянемо важливий випадок, коли область на площині задається лінійними нерівностями. Нехай маємо лінійну нерівність з двома змінними x, y: ax + by + c > 0 (1.1) Якщо x, y розглядати як координати точок на площині, то множина точок, координати яких задовольнюють (1.1), називається областю розв'язків цієї нерівності. Областю розв'язків (1.1) є півплощина.
Рис.1.4. Щоб дізнатись, яка з двох напівплощин відповідає нерівності (1.1), треба взяти пробну точку, яка не лежить на прямій ax + by + c = 0, наприклад, М0 (x0 , y0 ), підставити її координати в нерівність (1.1). Якщо нерівність (1.1) виконується, то точка М0 (x0 , y0 ) належить шуканій півплощині, якщо не виконується, то це друга півплощина. Коли пряма не проходить через початок координат, то зручно пробною точкою взяти початок координат О(0, 0). В випадку, коли задана система із m нерівностей:
a1 x + b1 y + c1 > 0, a2 x + b2 y + c2 > 0, (1.2.) ............... am x + bm y + cm > 0.
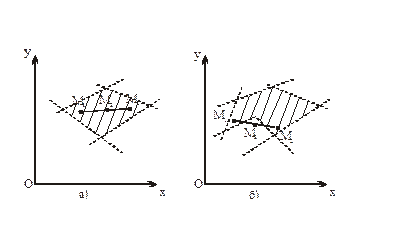
то геометрично отримаємо перетин півплощин, які можуть утворити многокутну область D. Така область називається областю розв'язків системи (1.2.). Ця область не завжди буває обмежена, вона може бути і необмеженою, і навіть порожньою. Останній випадок має місце, коли система нерівностей (1.2.) суперечлива. Область розв'язків системи нерівностей є опуклою, тобто якщо разом із будь-якими своїми двома точками вона містить і відрізок, що їх з'єднує. На рис. 1.5 зображені опукла і неопукла області. На рис. 1.5 а) разом з точками М1 і М2 даній області належить весь відрізок М1М2, область – опукла. На рис. 1.5 б) маємо випадок, коли крайні точки відрізка М1 і М2 належать області, однак існує точка М3 цього відрізка, яка даній області не належить. Ця область – неопукла.
Рис. 1.5. Опукла (а) та неопукла (б) області.
Зауважимо, що півплощина є опуклою областю. Має сенс підкреслити, що результат перетину опуклих областей є опукла область. Приклад 1.4. Знайти область розв'язків системи нерівностей:
Замінюючи нерівності рівняннями, отримаємо рівняння чотирьох прямих: x – 1 = 0 (1); y – 1 = 0; (2); x + y – 3 = 0; (3); -6x – 7y + 42 = 0 (4), які зображені на рис. 1.6.
Рис. 1.6.
На рис. 1.6 стрілками показані півплощини, які є розв'язками нерівностей, а сама область D заштрихована і є опуклою.
|
||||||||||
|
Последнее изменение этой страницы: 2016-12-16; просмотров: 234; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.211.246 (0.01 с.) |

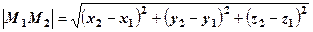
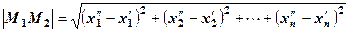
 розуміють круг, квадрат і т.п., що містять цю точку.
розуміють круг, квадрат і т.п., що містять цю точку. ).
).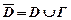 - замкнена область.
- замкнена область.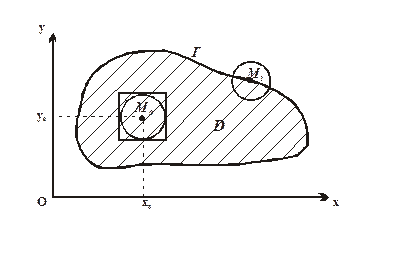


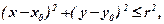
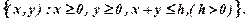
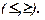

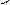
 x – 1 > 0; y – 1 > 0; x + y – 3 > 0;
x – 1 > 0; y – 1 > 0; x + y – 3 > 0;