Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Арістотель (384- 322 до н.е.) - грецький філософСодержание книги Поиск на нашем сайте
Арістотель (384- 322 до н.е.) - грецький філософ
...вивчення математики завжди сприяє розвитку строгості і ясності мислення. Картан, Анрі (нар. 1904) французький математик
А математику ще й тому вивчати слід, що вона розум до ладу приводить. Ломоносов М.В. (1711-1765) –вчений-енциклопедист, поет Жодне технічне вдосконалення неможливе без складних розрахунків. Але так само важко уявити розвиток будь-якої науки, включаючи суспільні, без використання досягнень сучасної математики і кібернетики. Математика, все глибше проникаючи в суміжні з нею і віддалені науки, стає непохитною опорою прогресу людських знань. Митропольський Ю.О, (нар. 1917) – український математик У вивчення природи математика робить найбільший вклад, бо вона розкриває впорядкований зв’язок ідей, за яким побудований Всесвіт. Прокл (410-485)-грецький філософ Тим, хто не знає математики, важко збагнути справжню, глибоку красу природи Фейнман Р. (нар. 1918) – американський фізик
І.Функції багатьох змінних
Числові множини, способи їх задання. Побудова області на площині
Числова множина – це множина, елементами якої є числа. Відомо, що N, Z, Q, I, R – множини натуральних, цілих, раціональних, ірраціональних та дійсних чисел. Їх прийнято зображати у вигляді точок на числовій осі. Якщо елементами множини є впорядкована пара чисел, то маємо множину точок М(х,у) на площині ХОУ, така множина позначається R2. У випадку, коли елементами множини є впорядковані трійки чисел, то маємо множину точок М(x,y,z) у просторі, яка позначається R3. Часто доводиться розглядати впорядковані набори більшої кількості чисел. Наприклад, якщо х і у – координати точки місцевості, z – висота над рівнем моря в цій точці, t – температура, p – атмосферний тиск, g - відносна вологість повітря, v – величина швидкості вітру, a - напрям вітру, то впорядкований набір із восьми чисел (x, y, z, t, p,g, v, a) характеризує метеорологічний стан в даній місцевості. У загальному випадку впорядкований набір із n чисел (х1, х2, …, хn) по аналогії із n=2, n=3 теж зручно називати точкою, а множина точок М(х1, х2, …, хn) утворює n-вимірний арифметичний простірRn. Дві точки M1(x1',x2',…,xn') і M2(x1'',x2'',…,xn'') збігаються між собою, якщо x1'= x1", …, xn'= xn".
Відомо, наприклад, що для двох точок М1(x1,y1,z1) і М2(x2,y2,z2) із простору R3 величина
є відстанню між цими точками. Подібним чином для двох точок М1 і М2, які належать Rn, величину
теж називають відстанню між точками М1 і М2. Окремі числові множини, як правило, задаються за допомогою нерівностей. Якщо всі нерівності строгі (<; >), то множина називається відкритою. Наприклад, інтервал: (a,b) = { x: a < x < b}; відкритий прямокутник: (a,b; c,d) = {(x,y): a<x<b, c<y<d}; відкритий паралелепіпед: (a,b; c,d; e,p) = {(x.y,z): a<x<b; c<y<d; e<z<p}. У загальному випадку можна говорити про відкритий n- вимірний паралелепіпед: (a1,b1; a2,b2; … an,bn ) = {(x1, x2, … xn): a1<x1<b1; a2<x2<b2; … an<xn<bn }. Cеред числових множин, які задаються нерівностями, часто зустрічаються також: (x-x0 )2 + (y-y0 )2 < r2 - відкритий круг у просторі R2 радіуса r з центром в точці М0 (x0 , y0 ); (x-x0 )2 + (y-y0 )2+ (z-z0 )2 < r2 - відкрита куля у просторі R3 радіуса r з центром в точці М0 (x0 , y0,z0 ); (x1-x10)2 + (x2-x20)2 + … + (xn-xn0)2 < r2 - відкрита куля в просторі Rn радіуса r з центром в точці М0 (x01 , х02, …, х0n ). Означення 1.1. Околом точки називається довільна відкрита множина, яка містить дану точку. У двовимірному випадку під околом точки
Означення 1.2. Множина точок називається зв'язною, якщо дві точки цієї множини можна з'єднати ламаною лінією, всі точки якої належать цій множині.
Означення 1.3. Точка М називається внутрішньою точкою множини D, якщо вона належить D разом з її достатньо малим околом.
Означення 1.4. Зв'язна множина, яка цілком складається із внутрішніх точок, називається областю. Означення 1.5. Граничною точкою області D називається точка, в будь-якому околі якої знаходяться точки, які як належать області D, так і не належать їй. Означення 1.6. Множина граничних точок області D називається її границею Г.
Означення 1.7. Область D разом з її границею Г називається замкненою областю D (позначається Посилаючись на геометричну інтуіцію, можна сказати, що якщо з геометричного тіла зідрати його границю, то отримаємо відкриту множину. На рисунку 1.1. точка М0 (x0 , y0 ) – внутрішня точка області D, точка М1 належить границі Г області D. Область D – відкрита, а область
Рис. 1.1.
На рисунку 1.1. окіл точки М0 (x0 , y0 ) зображений в вигляді круга і квадрата. Наприклад, замкнені області: сегмент: [a, b] = замкнений прямокутник: [a, b; с, d] = замкнений круг радіуса r з центром в точці М0 (x0, y0 ):
замкнений трикутник:
Таким чином, в замкнених областях обмеження задаються нестрогими нерівностями В подальшому для наочності будемо вивчати числову множину R2, тобто сукупність точок на площині. Для побудови області на площині треба знайти такі точки М(x,,y), координати яких задовольняли б нерівностям, які задають множину. Приклад 1.1. Побудувати область D на площині, яка задана нерівностями:
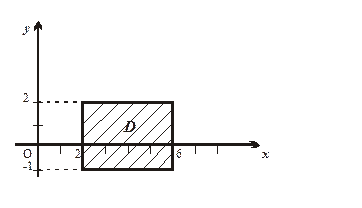
Даним нерівностям задовольняють координати точки, яка знаходиться всередині або на границі прямокутника, сторони якого лежать на прямих х = 2; х = 6; y = -1; y = 2. Цей прямокутник є замкненою областю (рис. 1.2)
Рис 1.2.
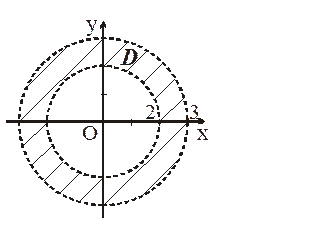
Приклад 1.2. Побудувати область D, яка задана нерівностями: 4 < x2 + y2 < 9. Даним нерівностям задовольняють координати точок, які знаходяться всередині кругового кільця, обмеженого колами x2 + y2 = 4 та x2 + y2 = 9 з центрами в точці О(0, 0) та радіусами r1 = 2, r2 = 3. Таким чином, це кругове кільце – відкрита область D (рис. 1.3).
Рис. 1.3.
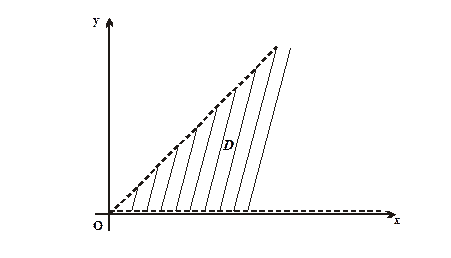
Приклад 1.3. Побудувати область D, задану нерівностями 0 < y < x В даному випадку маємо відкриту область D, яка обмежена прямими y = x та y = 0 (рис. 1.4.). Геометрично – це всі точки, що знаходяться внутрі кута. Точки, що розміщені на сторонах кута області D не належать, тому на рис.1.4 сторони кута зображені пунктиром. Розглянемо важливий випадок, коли область на площині задається лінійними нерівностями. Нехай маємо лінійну нерівність з двома змінними x, y: ax + by + c > 0 (1.1) Якщо x, y розглядати як координати точок на площині, то множина точок, координати яких задовольнюють (1.1), називається областю розв'язків цієї нерівності. Областю розв'язків (1.1) є півплощина.
Рис.1.4. Щоб дізнатись, яка з двох напівплощин відповідає нерівності (1.1), треба взяти пробну точку, яка не лежить на прямій ax + by + c = 0, наприклад, М0 (x0 , y0 ), підставити її координати в нерівність (1.1). Якщо нерівність (1.1) виконується, то точка М0 (x0 , y0 ) належить шуканій півплощині, якщо не виконується, то це друга півплощина. Коли пряма не проходить через початок координат, то зручно пробною точкою взяти початок координат О(0, 0). В випадку, коли задана система із m нерівностей:
a1 x + b1 y + c1 > 0, a2 x + b2 y + c2 > 0, (1.2.) ............... am x + bm y + cm > 0.
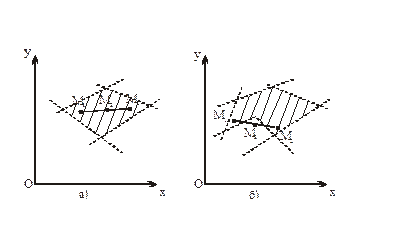
то геометрично отримаємо перетин півплощин, які можуть утворити многокутну область D. Така область називається областю розв'язків системи (1.2.). Ця область не завжди буває обмежена, вона може бути і необмеженою, і навіть порожньою. Останній випадок має місце, коли система нерівностей (1.2.) суперечлива. Область розв'язків системи нерівностей є опуклою, тобто якщо разом із будь-якими своїми двома точками вона містить і відрізок, що їх з'єднує. На рис. 1.5 зображені опукла і неопукла області. На рис. 1.5 а) разом з точками М1 і М2 даній області належить весь відрізок М1М2, область – опукла. На рис. 1.5 б) маємо випадок, коли крайні точки відрізка М1 і М2 належать області, однак існує точка М3 цього відрізка, яка даній області не належить. Ця область – неопукла.
Рис. 1.5. Опукла (а) та неопукла (б) області.
Зауважимо, що півплощина є опуклою областю. Має сенс підкреслити, що результат перетину опуклих областей є опукла область.
Приклад 1.4. Знайти область розв'язків системи нерівностей:
Замінюючи нерівності рівняннями, отримаємо рівняння чотирьох прямих: x – 1 = 0 (1); y – 1 = 0; (2); x + y – 3 = 0; (3); -6x – 7y + 42 = 0 (4), які зображені на рис. 1.6.
Рис. 1.6.
На рис. 1.6 стрілками показані півплощини, які є розв'язками нерівностей, а сама область D заштрихована і є опуклою. Лінії та поверхні рівня Означення 2.1. Змінна величина Z називається функцією двох змінних x і y, якщо кожній парі чисел (x, y) (або кожній точці М(x, y)) з деякої множини D площини xOy ставиться у відповідність визначене значення змінної Z. Позначається Z = f(x, y) або Z = f (M).
Наприклад. 1) Площа прямокутника S = xy є функцією двох змінних x і y – довжин відповідних сторін; 2) Об'єм конуса V = 1/3 p R2h – функція радіуса основи R і висоти h.
Означення 2.1. узагальнюється на більшу кількість змінних.
Означення 2.2. Змінна Z називається функцією незалежних змінних x1, x2 , … xn з деякої множини D, що належить n -вимірному простору Rn, якщо кожній точці М(x1, x2 , … xn) Z = f (M) = f (x1, x2 , … xn). Наприклад: 1) Температура Т в даній точці М залежить від її координат x, y, z, а також від моменту часу t, в який вона вимірюється, тобто T = f (x, y, z, t). 2) Очікуваний прибуток Р від споруджуваного промислового об'єкта є функцією затрат на його будівництво, часу t від початку будівництва до початку випуску продукції, від величини попиту Q на цю продукцію та інших економічних факторів.
Означення 2.3. Множина D точок, в яких функція визначена називається областю визначення або областю існування функції, а множина Е, яка складається із значень функції, називається множиною значень функції f (M). У випадку n = 2 функція двох змінних Z = f (x, y) може розглядатися як функція точки площини в тривимірному просторі R3. Графіком функції Z = f (x, y) є геометричне місце точок (x, y,) f (x, y)), яке описує деяку поверхню в просторі R3. Приклад 2.1. Знайти область визначення і множину значень функції
Рис 2.1
Приклад 2.2. Знайти область визначення поданих функцій: 1) 2) 3) 4) 1). Розв’язання для
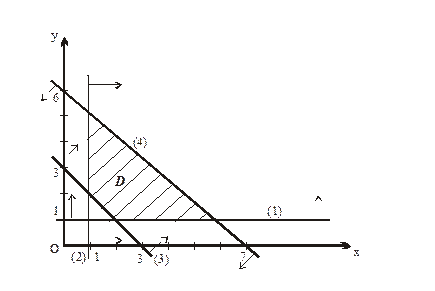
1. Нагадаємо, що елементарна функція 2. Складаємо аналогічну нерівність для заданої функції двох змінних: (1) 3. Замінимо останні нерівності рівняннями, отримаємо рівняння границі області визначення: х=2 – пряма, перпендикулярна осі ОХ, у=1 – пряма, перпендикулярна осі ОУ. Будуємо їх в системі ХОУ (див. рис. 2.2) 4. Відносно прямих х=2 і у=-1 вибираємо ті частини площини ХОУ, де виконуються нерівності (1) або (2).
Рис. 2.2.
2). Розв’язання для функції 1. Елементарна функція однієї змінної y=lg x визначена, якщо x>0. 2. Аналогічна нерівність для функції
3. Замінимо в (3) нерівність рівнянням: 4. Пробна точка О(0;0) задовольняє нерівність (3)
Отже, О(0;0) належить області розв’язків нерівності (3). Тобто вся область визначення – це множина точок, які лежать у середині заданого круга, виключаючи границю
Рис 2.3
3) Розв’язання для функції 1. Відповідною елементарною функцією однієї змінної є 2. Аналогічна нерівність для функції
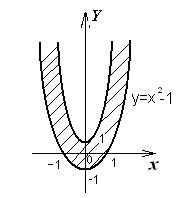
3. Замінивши нерівності на рівняння, отримаємо дві параболи 4. Пробна точка О(0,0) задовольняє ліву а також і праву нерівності (4)
Тобто початок координат знаходиться нижче першої параболи
Рис. 2.4 4) Розв’язання для функції 1. Відповідна функція однієї змінної 2. Для функції
3. Рівняння
півосі цього еліпса
4. Пробна точка О(0,0) нерівність (5) не задовольняє, бо нерівність
Рис 2.5
Приклади для самостійного розв’язання: Знайти область визначення функції: 1. 4. Відповіді. 1. Множина точок, які розміщені між віссю ОУ вище вітки параболи 3. Множина точок Означення 2.4. Лінією рівня функції Z = f (x, y) називається лінія f (x, y) = С на площині xOy, в точках якої функція має стале значення Z = C.
Означення 2.5. Поверхнею рівня функції U = f (x, y, z) називається поверхня f (x, y, z) = С, в точках якої функція має стале значення U = C. Приклад 2.3. Знайти лінії рівня функції
Рівняння ліній рівня (C > 0). Якщо С приймає дійсні значення, то отримуємо концентричні кола з центром в точці О(0,0), радіуса
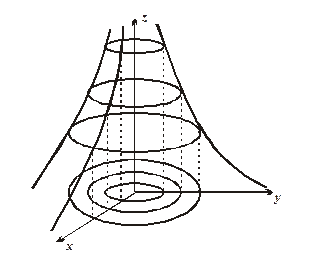
Зауважимо, що за допомогою ліній рівня f (x, y) = С можна побудувати поверхню Z = f (x, y) (рис. 2.2)
Рис. 2.6. Основними способами задання функції двох змінних є такі: 1) аналітичний, тобто за допомогою аналітичного виразу(формули); 2) табличний, за допомогою таблиці з двома входами, де кожній парі чисел
3) графічний, графіком функції двох змінних може бути деяка поверхня ...... xn ® an Приклад 3.1. З'ясувати, чи має функція
x2 – y2
x2 + y2 границю при x ® 0, y ® 0.
Нехай точка M(x, y) прямує до точки O(0, 0) по прямій y = kx. Тоді: x2 – y2 x2 – k2 x2 1 – k2 1 – k2
x ® 0x2 + y2 x ® 0 x2 + k2 x2 x ® 0 1 + k2 1 + k2 y ® 0 Результат залежить від k, тому функція не має границі. Приклад 3.2. Обчислити границю x2 + y2
y ® 0
Для обчислення границі перейдемо до полярних координат: x = r cos j; y = r sin j.
Тоді x2 + y2 = r2, і тому маємо:
x2 + y2 r2 0
y ® 0 0 < j < 2p
r ® 0r2 r ® 0 Таким чином, при будь-якому прямуванні М (x, y) до О (0, 0) маємо число 2, тобто границя дорівнює 2. Разом з поняттям кратної границі функції можна розглянути повторні границі, які обчислюються послідовно. Наприклад, для функції двох змінних: lim f (x, y) = A; lim lim f (x, y) = B; lim lim f (x, y) = C x ® x0 x ® x0 y ® y0 y ® y0 x ® x0 y ® y0 В загальному випадку А ¹ В ¹ С. Очевидно, якщо границя існує, то А = В = С. Означення 3.2. Функція Z = f (M) називається неперервною в точці M0, якщо виконуються умови: 1) функція визначена в точці М0, тобто існує f (M0); 2) існує lim f (M); M ® M0 3) виконується рівність
Означення 3.3. Функція називається неперервною в області, якщо вона неперервна в кожній точці цієї області. Якщо хоча б одна із умов 1) – 3) означення 3.2 не виконується, то точка М0 називається точкою розриву функції. Точки розриву функції можуть бути ізольованими, утворювати лінії розриву, поверхні розриву. Приклад 3.3. Знайти точки розриву функції: Xy
2x + 3y + 4 Функція невизначена в точках, де знаменник дорівнює нулю. Тому маємо лінію розриву - пряму 2x + 3y + 4 = 0.
Диференціали вищих порядків
В §5 для функції двох змінних z=f (x,y) було встановлено формулу повного диференціала
або його ще називають диференціалом І-го порядку. За означенням диференціалом ІІ-го порядку називається диференціал від диференціала І-го порядку, тобто:
За формулою (7.1) маємо:
при цьому прийнято скорочено писати (dx)2=dx2, (dy)2=dy2. Аналогічно вводяться диференціали d3f, d4f і т.д. Для отримання виразів для диференціалів вищих порядків зручно скористатися таким підходом. Запишемо формально диференціал І-го порядку для функції z=f(x,y) у вигляді:
де вираз
називається оператором повного диференціала. За його допомогою вводиться оператор диференціала ІІ порядку:
Очевидно, що застосовуючи останній оператор до функції z=f(x,y), отримаємо формулу (7.2). Аналогічно, за допомогою оператора
можна записати диференціал ІІІ-го порядку
і т.д. В замкнутій області Нехай функція Приклад. Знайти найбільше значення добутку Розв'язання. Покажемо, що найбільше значення Знайдемо
Маємо функцію від незалежних змінних Геометрично - ця область є прямокутний трикутник, обмежений прямими Знайдемо похідні і прирівняємо до нуля:
Внутрі області розв'язком системи є Враховуючи, що на границі області Задача розв'язана, тому що при Умовний екстремум Локальний екстремум функції двох змінних без будь-яких додаткових умов називається безумовним. Якщо знаходиться екстремум функції за деяких додаткових умов, то він називається умовним. Нехай треба знайти екстремум функції
Рис.13.1.
Побудуємо допоміжну функцію трьох змінних, яка називається функцією Лагранжа: Необхідні умови екстремуму цієї функції мають вигляд:
Для встановления виду умовного екстремуму досліджують знак другого повного диференціала функції Лагранжа
в знайдених із системи (13.2) критичних точках при умові, що
Тоді функція Приклад 11.1. Знайти екстремум функції За методом Лагранжа: Запишемо необхідні умови екстремуму:
Звідки: Знайдемо другий диференциал функції Лагранжа. Оскільки
Отже, функція
Метод найменших квадратів При вивченні закономірностей в деяких дослідженнях інженерної справи, економіки, біології, медицини і т.п. приходиться аналітично описувати (у вигляді формули) зв'язок між двома змінними x та y. Для цього в процесі експериментів, спостережень вимірюють з можливою точністю окремі значення xi і відповідні їм значення yi (i=1,2,…,n), або отримують такі значення як статистичні дані. В результаті маємо таблицю значень (табл. 1).
Таблиця 1
Подібну таблицю можна отримати, наприклад, при дослідженні лінійного розширення стержня в залежності від температури, якщо коефіцієнт лінійного розширення данного матеріалу невідомий, тоді x1, x2,…, xn – виміряні значення температури, а y1, y2,…,yn – відповідні їм значення довжини. Побудуємо у вибраній системі координат XOY точки Mi(xi, yi), координати яки
|
||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-16; просмотров: 347; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.128.197.182 (0.016 с.) |

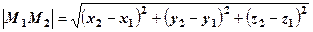
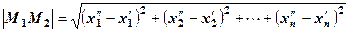
 розуміють круг, квадрат і т.п., що містять цю точку.
розуміють круг, квадрат і т.п., що містять цю точку. ).
).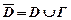 - замкнена область.
- замкнена область.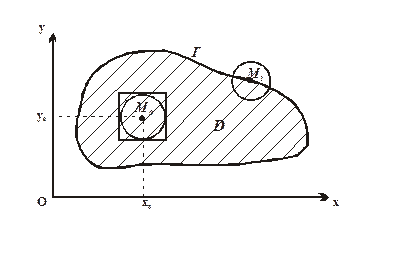


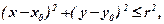
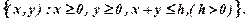
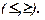

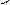
 x – 1 > 0; y – 1 > 0; x + y – 3 > 0;
x – 1 > 0; y – 1 > 0; x + y – 3 > 0;
 D ставиться у відповідність визначене значення змінної Z:
D ставиться у відповідність визначене значення змінної Z: .
.

 Функція Z має дійсні значення за умови 1 – x2 – y2 ≥ 0, або x2 + y2 < 1, тобто областю визначення даної функції є замкнений круг радіуса 1 з центром в точці О(0,0). Множиною значень функції є сегмент [ 0, 1 ], що випливає з виразу Z = Ö 1 – x2 – y2. Графіком функції є верхня напівсфера радіуса 1 з центром в точці О(0,0,0).
Функція Z має дійсні значення за умови 1 – x2 – y2 ≥ 0, або x2 + y2 < 1, тобто областю визначення даної функції є замкнений круг радіуса 1 з центром в точці О(0,0). Множиною значень функції є сегмент [ 0, 1 ], що випливає з виразу Z = Ö 1 – x2 – y2. Графіком функції є верхня напівсфера радіуса 1 з центром в точці О(0,0,0).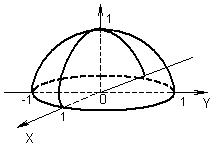
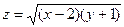 ;
;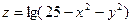 ;
; ;
; .
.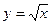 визначена, якщо
визначена, якщо  .
. , яка рівносильна двом системам нерівностей, а саме,
, яка рівносильна двом системам нерівностей, а саме,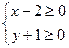 , або (2)
, або (2)  .
.
 . (3)
. (3)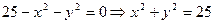 - коло радіуса 5 з центром в О(0;0), яке є границею області.
- коло радіуса 5 з центром в О(0;0), яке є границею області.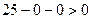
 , бо нерівність (3) строга (див. рис. 2.3).
, бо нерівність (3) строга (див. рис. 2.3).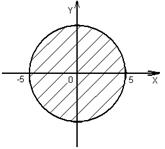
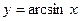 , яка існує для
, яка існує для 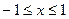 .
. . (4)
. (4) і
і  , які симетричні відносно осі ОУ з вітками напрямленими вверх, причому вершина першої з них в точці
, які симетричні відносно осі ОУ з вітками напрямленими вверх, причому вершина першої з них в точці 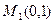 , а другої в точці
, а другої в точці  .
. ,
, 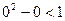
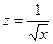 визначена для
визначена для  .
.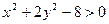 . (5)
. (5)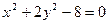 описує еліпс, канонічна форма якого:
описує еліпс, канонічна форма якого: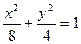 , (6)
, (6)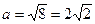 ,
,  .
. - невірна, тобто О(0,0), як внутрішня точка даної фігури, не входить у множину розв’язків нерівності (5). Множина розв’язків нерівності (5) – це всі точки, які лежать зовні еліпса. (див. рис. 2.4), не включаючи точок еліпса.
- невірна, тобто О(0,0), як внутрішня точка даної фігури, не входить у множину розв’язків нерівності (5). Множина розв’язків нерівності (5) – це всі точки, які лежать зовні еліпса. (див. рис. 2.4), не включаючи точок еліпса.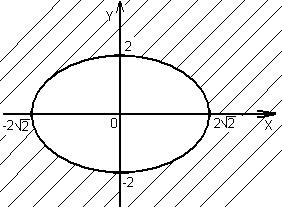

 2.
2. 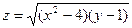 3.
3. 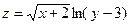
 5.
5. 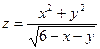 6.
6. 
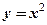 в першій чверті. 2. Множина точок
в першій чверті. 2. Множина точок  .
. . 4. Множина точок
. 4. Множина точок  , які розміщені на еліпсі
, які розміщені на еліпсі  та зовні його. 5. Множина точок
та зовні його. 5. Множина точок 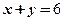 . 6. Областью визначення є смуга між двома паралельними прямими
. 6. Областью визначення є смуга між двома паралельними прямими 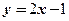 і
і  , включно з цими прямими.
, включно з цими прямими.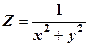
 мають вигляд
мають вигляд 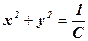
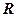 , де
, де  ..
..
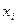 та
та 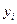 ставиться в таблиці відповідне значення
ставиться в таблиці відповідне значення 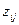
 Z =
Z =


 lim.
lim. x ® 0Ö x2 + y2 + 1 - 1
x ® 0Ö x2 + y2 + 1 - 1

 lim = lim = { } =
lim = lim = { } =
 x ® 0Ö x2 + y2 + 1 - 1 r ® 0 Ö r2 + 1 – 1 0
x ® 0Ö x2 + y2 + 1 - 1 r ® 0 Ö r2 + 1 – 1 0

 r2 Ö (r2 + 1 + 1)
r2 Ö (r2 + 1 + 1)
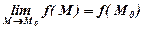 .
. 
 Z =.
Z =.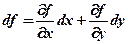 , (7.1)
, (7.1)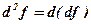 .
.
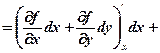
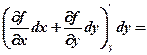
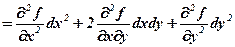 , (7.2)
, (7.2)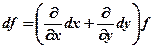 ,
, ,
, ,
, ,
,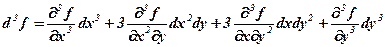 (7.3)
(7.3) визначена і неперервна в обмеженій замкненій області D і має в ній скінчені частинні похідні. В цій області знайдеться точка
визначена і неперервна в обмеженій замкненій області D і має в ній скінчені частинні похідні. В цій області знайдеться точка  в якій функція приймає найбільше (найменше) значення.Якщо точка
в якій функція приймає найбільше (найменше) значення.Якщо точка  лежить усерединє області D, то в ній функція має максимум (мінімум), тому ця точка знаходиться серед критичних точок. Але найбільшого (найменшого) значення функція може досягати і на границі області. Тому, для того щоб знайти найбільше (найменше) значення функції
лежить усерединє області D, то в ній функція має максимум (мінімум), тому ця точка знаходиться серед критичних точок. Але найбільшого (найменшого) значення функція може досягати і на границі області. Тому, для того щоб знайти найбільше (найменше) значення функції 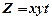 невід'ємних чисел
невід'ємних чисел 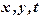 за умови, що їх сума є стала величина:
за умови, що їх сума є стала величина: 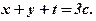
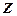 отримаємо при
отримаємо при 
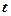 із даної умови:
із даної умови:  і підставимо в
і підставимо в 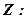
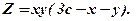
 в двовимірній області згідно умов:
в двовимірній області згідно умов: 
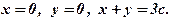
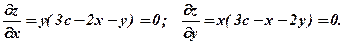
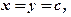 де
де 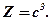
 то в знайденій точці
то в знайденій точці 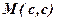 , дійсно функція має найбільше значення.
, дійсно функція має найбільше значення.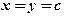 для змінної
для змінної 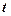 маємо
маємо 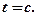 Згідно з результатом добуток невід'ємних чисел
Згідно з результатом добуток невід'ємних чисел  , сума яких дорівнює
, сума яких дорівнює 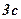 , не більше
, не більше 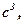 тобто
тобто 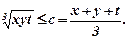 Отже середнє геометричне не більше середнього арифметичного. Це вірно для довільної кількості чисел.
Отже середнє геометричне не більше середнього арифметичного. Це вірно для довільної кількості чисел.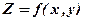 за умови
за умови 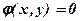 . Якщо вважати, що функція
. Якщо вважати, що функція  циліндр, то треба знайти екстремум не на всій поверхні, а тільки на лінії, яку вирізає з даної поверхні циліндрична поверхня (рис.13.1).
циліндр, то треба знайти екстремум не на всій поверхні, а тільки на лінії, яку вирізає з даної поверхні циліндрична поверхня (рис.13.1).
 (13.1)
(13.1) 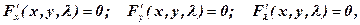 або:
або: (13.2)
(13.2)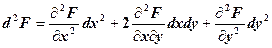
 і
і  зв’язані рівнянням
зв’язані рівнянням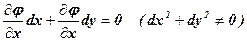 .
.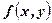 має умовний максимум, якщо
має умовний максимум, якщо  , і функція
, і функція 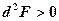 (див. 11.20)
(див. 11.20)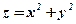 за умови
за умови 
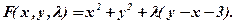


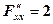 ,
,  ,
,  , то
, то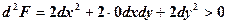 .
.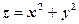 має умовний мінімум в точці
має умовний мінімум в точці  .
.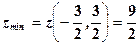 .
.