
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Екстремум функції двох зміннихСодержание книги Поиск на нашем сайте
Означення 1. Функція z=f(x,y) має максимум в точці Mо(xо,yо), якщо для всіх точок M(x,y), досить близьких до точки Mо(xо,yо) виконується нерівність
Означення 2. Функція z=f(x,y) має мінімум в точці Mо (xо ,yо ), якщо для всіх точок M(x,y), досить близьких до точки Mо (xо ,yо ), виконується нерівність
Точки максимума і мінімума функції мають спільну назву точок екстремуму. Коли говорять, що функція має екстремум, то це означає, що вона має в цій точці максимум або мінімум. Як і для функції однієї змінної, у двовимірному випадку теж виділяють необхідні і достатні умови екстремуму. 1О. Необхідні умови існування екстремуму. Теорема 11.1. Якщо в точці екстремуму Mо (xо ,yо ) функція z=f(x,y) має перші частинні похідні, то вони в цій точці перетворюються в нуль, тобто
Доведення. Із означення екстремуму випливає, що функція однієї змінної z=f(x,yо ) при фіксованому y=yо має екстремум при x=xо. Згідно необхідної умови екстремуму для функції однієї змінної маємо
Аналогічно приходимо до умови
Геометрично це означає, що дотичні прямі, проведені в точці екстремуму до лінії z=f(x,yо) і z=f(xо,y), паралельні відповідним координатним осям оХ і оY (див. рис.11.1). Однак у випадку сідлової поверхні (див. рис.11.2) паралельність осям описаних дотичних в точці поверхні не свідчить про те, що це точка екстремуму. Тому умови (11.1) є тільки необхідними, але не достатніми.
Рис.11.1. Рис.11.2. Точки, в яких частинні похідні дорівнюють нулю, або не існують, називаються критичними точками функції. Далі установимо достатні умови екстремуму, яким задовільняє функція в критичних точках.
2О. Достатні умови існування екстремуму Спочатку введемо деякі скорочені позначення. Нехай Mо(xо,yо) - критична точка функції z=f(x,y), в якій
Т еорема 11.2. Якщо для функції z=f(x,y) виконуються необхідні умови екстремуму в точці 1) має екстремум при 2) немає екстремуму за умови 3) при Доведення. Скористаємось формулою Тейлора (див.8, формулу (8.3)) при n=3.
Перенесемо доданок
Тому
Можна довести, що доданок За формулою другого диференціалу (див.формулу (7.2)) маємо
а згідно зроблених позначень
Таким чином, знак виразу
Отже задача зводиться до знаку дослідження квадратного тричлена Відомо, що квадратний тричлен зберігає знак, якщо його дискримінант від'ємний:
Причому, якщо
Якщо ж
За умови Приклад. Дослідити на екстремум функцію Розв'язання. Для знаходження критичних точок скористаємось теоремою 11.1, згідно з якою отримуємо систему рівнянь:
Розв'яжемо цю систему:
Маємо
Тоді в точці
В точці
|
|||||||
|
Последнее изменение этой страницы: 2016-12-16; просмотров: 373; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.116.142 (0.008 с.) |

 .
. .
. (11.1)
(11.1)


 ,
,  . Припустимо, що існують неперервні частинні похідні другого і третього порядків і позначимо
. Припустимо, що існують неперервні частинні похідні другого і третього порядків і позначимо
 , тобто
, тобто  ,
,  , то в цій точці функція:
, то в цій точці функція: , причому максимум, якщо А<0, і мінімум, якщо А>0;
, причому максимум, якщо А<0, і мінімум, якщо А>0; ;
; екстремум може бути і може не бути, в цьому випадку потрібні додаткові дослідження.
екстремум може бути і може не бути, в цьому випадку потрібні додаткові дослідження.
 в ліву частину рівності і позначимо
в ліву частину рівності і позначимо  - приріст функції. Якщо в точці
- приріст функції. Якщо в точці  максимум, то
максимум, то  , якщо ні – мінімум, то
, якщо ні – мінімум, то 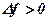 . Згідно умови теореми 2
. Згідно умови теореми 2 .
. (11.2)
(11.2) є нескінченно малою величиною вищого порядку в порівнянні з доданком
є нескінченно малою величиною вищого порядку в порівнянні з доданком  при
при  ,
,  . Тому головною частиною приросту функції
. Тому головною частиною приросту функції  у формі (11.2) є другий диференціал, і його знаком визначається знак приросту
у формі (11.2) є другий диференціал, і його знаком визначається знак приросту  ,
,
 залежить від співвідношення двох змінних величин
залежить від співвідношення двох змінних величин  і
і  (разом з їхніми знаками). Щоб звести до однієї змінної, винесемо за дужки
(разом з їхніми знаками). Щоб звести до однієї змінної, винесемо за дужки  (при
(при  ) і залишимо
) і залишимо  , тобто
, тобто .
. .
.
 , то
, то  , а значить
, а значить
 , то
, то
 .
.

 і
і  дві критичні точки. Знайдемо тепер похідні другого порядку:
дві критичні точки. Знайдемо тепер похідні другого порядку:


 >
>  отже екстремум в т.
отже екстремум в т.  відсутній.
відсутній. маємо:
маємо: 
 <
<  екстремум існує і поскільки
екстремум існує і поскільки  >
> 



