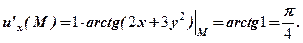Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Частинні похідні, їх геометричний змістСодержание книги Поиск на нашем сайте
Нехай задана функція двох змінних Z = f (x, y). Будемо надавати змінним x і y прирости Dx і Dy. Величина DZ = f (x + Dx, y + Dy) – f (x, y) називається повним приростом функції. Величина Dx Z = f (x + Dx, y) – f (x, y) називається частинним приростом функції по змінній х. Dу Z = f (x, y + Dу) – f (x, y) частинний приріст функції по змінній у.
Означення 4.1. Частинною похідною функції двох змінних по одній із змінних х чи у називається границя відношення відповідного частинного приросту функції до приросту аргумента по цій змінній при прямуванні останнього до нуля (якщо ця границя існує), тобто:
Dx Z f (x + Dx, y) – f (x, y)
Dx ® 0 Dx Dx ® 0 Dx - частинна похідна по х,
Dy Z f (x, y + Dy) – f (x, y)
Dy ® 0 Dy Dy ® 0 Dy - частинна похідна по у. Є інші позначення:
Знак " º " означає тотожні рівності, позначення. Аналогічне узагальнення має місце для функції багатьох змінних.
Означення 4.2. Нехай M (x1 , x2 , …, xn) - довільна фіксована точка із області визначення функції Z = f (x1 , x2 , …, xn) надаючи змінній хk (k = 1, 2, …, n) приріст Dxk, розглянемо границю:
Ця границя називається частинною похідною данної функції по змінній xk в точці М і позначається
Частинні похідні знаходяться за звичайними правилами і формулами диференціювання (при цьому усі змінні, крім xk, розглядаються як сталі).
Приклад 4.1. Знайти частинні похідні функції: Z = arctg Вважаючи у сталою, маємо:
Якщо ж взяти х – сталим, то аналогічно:
Для функції Z = f (x, y) легко вияснити геометричний зміст похідних. Геометричним зображенням даної функції є деяка поверхня Р (рис.4.1).
Рис.4.1.
Вважаючи у = const, ми отримуємо плоску криву Гх , яка є перетином поверхні Р площиною, що паралельна координатній площині хОz. Нехай МК – дотична до кривої Гх в точці М (x, y, z) і a є кут, утворений цією дотичною з віссю Ох. Згідно з геометричним змістом звичайної похідної маємо:
Аналогічно, якщо Гy є перетин поверхні Р площиною х = const і b є кут, утворений з віссю Оу дотичною МL в точці М (x, y, z) до кривої Гу, то
Зауваження 1. При знаходженні частинних похідних функції багатьох змінних ми застосовуємо всі правила і формули таблиці похідних, які відносились для функції однієї змінної.
2. При знаходженні частинної похідної від функції, наприклад, двох змінних Якщо частинна похідна знаходиться по у, то х вважається сталою.
Приклади. Знайти частинні похідні функцій. 1. 3. 5. Обчислити значення частинних похідних Розв’язання. 1. Аналогічно, 2. 3.
4.
5.
|
||||||||
|
Последнее изменение этой страницы: 2016-12-16; просмотров: 337; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.91.78 (0.009 с.) |


 Z'x = lim = lim -
Z'x = lim = lim -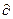 z
z 
 Z'x º º º f 'x (x, y);
Z'x º º º f 'x (x, y);
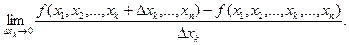

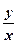 .
.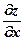 =
= 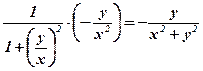 .
. =
= 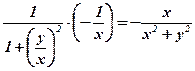 .
.
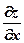 = tg a.
= tg a. по змінній х будемо розглядати у як сталу величину.
по змінній х будемо розглядати у як сталу величину.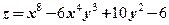 , 2.
, 2. 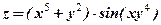 ,
, , 4.
, 4. 
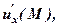
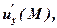
 функції
функції 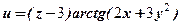 в точці
в точці 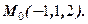
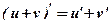 ,
, 

 Вважаючи у сталою, знаходимо
Вважаючи у сталою, знаходимо 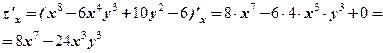 .
.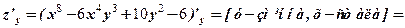

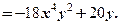
 ,
, 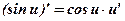 . Отже, маємо
. Отже, маємо 
 .
.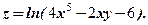 Відомо, що
Відомо, що 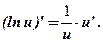 Далі маємо
Далі маємо
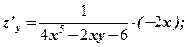
 .
. 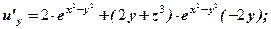
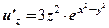 .
.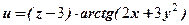 , М(-1,1,2). Оскільки
, М(-1,1,2). Оскільки  , то
, то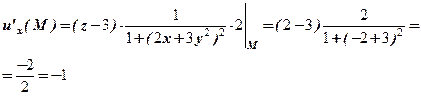 ;
;