
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Найбільше і найменше значення функції в областіСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Якщо функція Для знаходження найбільшого і найменшого значень функції в області потрібно знайти всі критичні точки всередині області, обчислити значення функції в цих точках, потім знайти найбільше і найменше значення функції на границі області і з усіх отриманих таким чином значень вибрати найбільше і найменше. Приклад 4.8. Знайти найбільше і найменше значення функції
Розв’язання. Досліджуючи цю функцію на екстремум знайдемо чотири критичні точки На На границях відрізка Порівнюючи знайдені значення, дійдемо висновку, що найбільше значення функції
Метод найменших квадратів Часто при розв'язку практичних задач функціональна залежність між змінними задається у вигляді таблиці:
Для аналізу отриманого розв'язку зручно підібрати функцію, яка відповідала б таблиці експериментальних даних і якою можна було б скористатися для одержання значень функції. Зобразивши точки Так, якщо точки таблиці групуються біля деякої прямої, цю функцію можна шукати у вигляді лінійної функції Якщо ж точки розташовуються біля деякої параболи, то природно шукати функцію у вигляді квадратичної функції Якщо є вигляд функції, то залишається підібрати такі її коефіцієнти, при яких функція найкраще відповідала б таблиці. Підбор значень коефіцієнтів здійснюється методом найменших квадратів, що полягає в наступному: складають суму квадратів різниць значень функції в точках Нехай, наприклад, функція Ця функція з двома змінними
Перепишемо систему у вигляді
Система (4.14) є системою лінійних рівнянь відносно Приклад 4.9. Досліджуючи залежність врожайності від кількості внесених добрив (y – врожайність у ц/га, x – кількість добрив у ц/га) одержали такі дослідні дані:
Розв’язання. Побудуємо дослідну лінію залежності Як бачимо з рисунка, на проміжку Складемо для нашої задачі і розв’яжемо систему (4.14). Для цього скористаємося розрахунковою таблицею:
Знаходимо Система (4.14) набуває вигляду
Розв’язуючи систему, знайдемо, що Нехай тепер У цьому випадку сума квадратів відхилень значень функції: Функція
то система рівнянь для визначення коефіцієнтів набуває вигляду:
Перепишемо систему інакше:
Із системи (4.15) коефіцієнти
Економічні задачі Нехай задана виробнича функція Вираз Еластичність виробничої функції Якщо виробнича функція встановлює залежність випуску Приклад 4.10. Для випуску деякого товару визначена виробнича функція Розв’язання. Для визначення зміни виробничої функції за чинниками
За означенням еластичність функції за кожним з чинників така:
Обчислимо коефіцієнти еластичності при
Таким чином, зі збільшенням чинника При збільшенні чинника Відзначимо, що від'ємне значення коефіцієнта еластичності показує зменшення виробничої функції при збільшенні відповідного чинника. Наприклад, якщо Приклад 4.11. Фірма реалізує частину товару на внутрішньому ринку, а іншу частину поставляє на експорт. Зв'язок ціни товару Розв’язання. Сумарний доход:
В обох випадках ціна береться з відповідних кривих попиту.
Одержуваний фірмою прибуток
Знаходимо частинні похідні першого порядку:
Стаціонарна точка Обчислюємо частинні похідні другого порядку:
Виходить, у стаціонарній точці існує максимум. Знайдемо оптимальні ціни для продажу на внутрішньому і зовнішньому ринках, підставляючи координати точки максимуму в криві попиту:
Підраховуємо максимальний прибуток при оптимальних об'ємах продажу на внутрішньому і зовнішньому ринках:
Приклад 4.12. Фірма робить два види товарів
Потрібно знайти такі значення Розв’язання. Сумарний доход від продажу товарів
Прибуток
Це і є функція, максимум якої потрібно знайти. Для знаходження стаціонарних точок, визначаємо частинні похідні першого порядку від функції
Стаціонарна точка
Таким чином, точка
Вправи 4.1. Знайти область визначення функції і побудувати її на площині: а) 4.2. На площині а) 4.3–4.12. Знайти частинні похідні першого порядку. 4.3. 4.5. 4.7. 4.9. 4.11. 4.13. Знайти повні диференціали функцій: а) г) 4.14. Обчислити приблизно за допомогою повного диференціала: а) 4.15. Знайти похідну функцію 4.16. Знайти градієнт функції 4.17. Знайти напрямок найбільшої зміни функції 4.18. Знайти похідні другого порядку функцій: а) г) 4.19. Дослідити функції на екстремум: а) в) д) 4.20. Наводяться дані про ріст продуктивності праці і зниження собівартості продукції по підприємству за 5 років стосовно базисного періоду, прийнятому за одиницю:
Лінійна залежність зниження собівартості від росту продуктивності праці 4.21. Нехай а) б) г) д) є) ж) 4.22. Потік пасажирів 4.23. Фірма виробляє два види товарів в кількостях 4.24. Є такі дані про ціну на нафту
Припускаючи, що між змінними 4.25. Фірма виробляє два види товарів 4.26. Сумарний прибуток підприємства залежить від виду двох ресурсів а) б) в) г) 4.27. Річні видатки підприємства можуть бути виражені функцією 4.28. Фірма вирішила щомісяця вкладати 10000 грош. од. на виробництво деякої продукції. Нехай середня заробітна платня по фірмі складає 200 грош. од., а вартість одиниці сировини дорівнює 100 грош. од. Визначити яку кількість робочих 4.29. Функція корисності має вигляд 4.30. Функція витрат а) б)
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 668; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.192.250 (0.011 с.) |

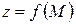 визначена і неперервна в замкнутій обмеженій області
визначена і неперервна в замкнутій обмеженій області  , то вона набуває в цій області свого найбільшого і найменшого значень.
, то вона набуває в цій області свого найбільшого і найменшого значень. в замкнутій області, обмеженої лініями
в замкнутій області, обмеженої лініями 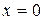 ,
, 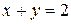 ,
, 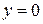 (рис.4.5).
(рис.4.5). Рис. 4.5.
Рис. 4.5.
 ,
,  ,
, 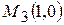 ,
,  , з яких лише одна точка
, з яких лише одна точка 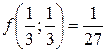 . Дослідимо функцію на границі області.
. Дослідимо функцію на границі області. маємо
маємо  . На
. На  маємо
маємо  маємо
маємо 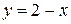 і функція набуває вигляду
і функція набуває вигляду 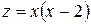 причому
причому  . Похідна цієї функції
. Похідна цієї функції  при
при  . Значення функції в цій точці
. Значення функції в цій точці 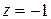 .
. і
і 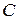 значення функції
значення функції  .
. в даній області досягається всередині області в точці
в даній області досягається всередині області в точці 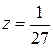 . Найменшого значення функція набуває на межі області у точці
. Найменшого значення функція набуває на межі області у точці  , тут
, тут  на координатній площині, можна зробити висновок про вигляд функції
на координатній площині, можна зробити висновок про вигляд функції  .
.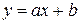 .
.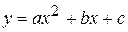 і т.д.
і т.д. і табличних значень
і табличних значень  , а потім підбирають коефіцієнти функції так, щоб ця сума була найменшою.
, а потім підбирають коефіцієнти функції так, щоб ця сума була найменшою. – лінійна, тобто
– лінійна, тобто  . Тоді
. Тоді 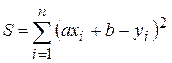 .
.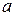 і
і  набуває мінімуму в точках, для яких
набуває мінімуму в точках, для яких  і
і  , тобто
, тобто
 (4.14)
(4.14) Рис. 4.6.
Рис. 4.6.
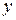 від
від 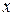 (рис. 4.6).
(рис. 4.6). залежність
залежність  буде досить точно відображатися лінійною функцією
буде досить точно відображатися лінійною функцією 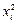
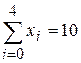 ,
,  ,
, 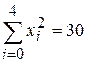 ,
,  .
. або
або 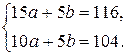
 ;
;  . Отже, залежність врожайності від кількості внесених добрив на 1 га найкраще відображає лінійна функція вигляду
. Отже, залежність врожайності від кількості внесених добрив на 1 га найкраще відображає лінійна функція вигляду  .
.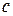 , при яких функція
, при яких функція  є функцією трьох змінних
є функцією трьох змінних  досягає мінімуму в точках, для яких
досягає мінімуму в точках, для яких  . Оскільки
. Оскільки ,
,  ,
, ,
,
 (4.15)
(4.15) , що виражає залежність, наприклад, витрат виробництва від кількості двох видів продукції
, що виражає залежність, наприклад, витрат виробництва від кількості двох видів продукції  , тоді виробнича функція зміниться на
, тоді виробнича функція зміниться на 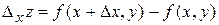 .
. відображає середній приріст виробничої функції на одиницю приросту чинника
відображає середній приріст виробничої функції на одиницю приросту чинника  , одержимо граничні витрати виробництва на одиницю продукції
, одержимо граничні витрати виробництва на одиницю продукції  . Аналогічно за чинником
. Аналогічно за чинником  .
. і вказує приблизно процентний приріст виробничої функції (підвищення, зниження), що відповідає приросту чинника
і вказує приблизно процентний приріст виробничої функції (підвищення, зниження), що відповідає приросту чинника 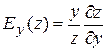 і вказує приблизно відсотковий приріст виробничої функції, що відповідає приросту чинника
і вказує приблизно відсотковий приріст виробничої функції, що відповідає приросту чинника  виробничих чинників
виробничих чинників  ,
,  ,...,
,...,  у вигляді
у вигляді  , то диференціальними характеристиками такої функції є:
, то диференціальними характеристиками такої функції є:  – гранична ефективність відносно чинника
– гранична ефективність відносно чинника  – еластичність випуску
– еластичність випуску  , де
, де  .
.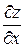 і
і  :
: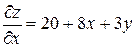 ;
;  .
. ;
;  .
.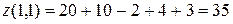 :
: ,
, 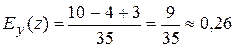 .
. і
і 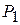 і його кількості
і його кількості  , проданого на внутрішньому ринку, описується рівнянням кривої попиту:
, проданого на внутрішньому ринку, описується рівнянням кривої попиту:  . Аналогічно для експорту ціна
. Аналогічно для експорту ціна  і кількість
і кількість  також зв'язані відношенням (рівнянням кривої попиту):
також зв'язані відношенням (рівнянням кривої попиту):  . Сумарні витрати визначаються виразом:
. Сумарні витрати визначаються виразом:  . Яку цінову політику повинна проводити фірма, щоб прибуток був максимальний?
. Яку цінову політику повинна проводити фірма, щоб прибуток був максимальний?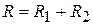 , де
, де  ,
,  – доходи від продажу на внутрішньому ринку і від експортних постачань відповідно:
– доходи від продажу на внутрішньому ринку і від експортних постачань відповідно: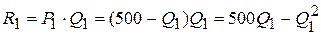 ,
, .
. .
.
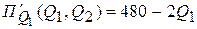 ,
,  ,
,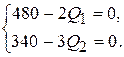
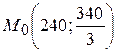 .
. ,
, 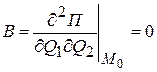 ,
, 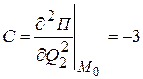 ,
,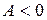 ,
, 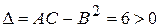 .
.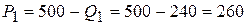 ,
, .
.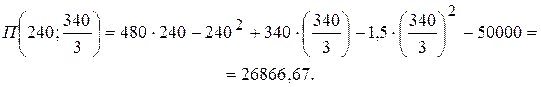
 і
і  і продає їх за ціною 1000 грош. од. і 800 грош. од. відповідно. Об'єми випуску товарів –
і продає їх за ціною 1000 грош. од. і 800 грош. од. відповідно. Об'єми випуску товарів –  .
. .
. являє собою різницю між доходом
являє собою різницю між доходом 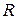 і витратами
і витратами  , тому
, тому  ,
, .
. і прирівнюємо їх до нуля:
і прирівнюємо їх до нуля: ,
,  ,
,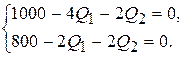
 . Знаходимо частинні похідні другого порядку:
. Знаходимо частинні похідні другого порядку: ,
,  ,
,  ,
,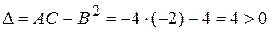 .
. ,
,  . Знайдемо суму максимального прибутку:
. Знайдемо суму максимального прибутку:
 ; б)
; б)  ; в)
; в) 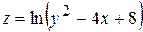 .
. побудувати сімейство ліній рівня:
побудувати сімейство ліній рівня: ; б)
; б)  .
. . 4.4.
. 4.4.  .
. . 4.6.
. 4.6. 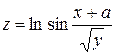 .
. . 4.8.
. 4.8. 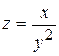 .
. . 4.10.
. 4.10.  .
.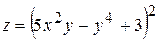 . 4.12.
. 4.12.  .
.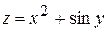 ; б)
; б)  ; в)
; в)  ;
; ; д)
; д)  .
. ; б)
; б)  ; в)
; в)  .
. в напрямку прямої
в напрямку прямої 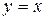 у точці
у точці  .
. в точці
в точці  .
. в точці
в точці  .
. ; б)
; б) 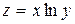 ; в)
; в)  ;
; ; д)
; д)  ; б)
; б)  ;
; ; г)
; г) 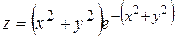 ;
; .
.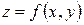 – виробнича функція. Знайти закон зміни виробничої функції за кожним з чинників,
– виробнича функція. Знайти закон зміни виробничої функції за кожним з чинників,  і
і  , коефіцієнти еластичності по витратах точці
, коефіцієнти еластичності по витратах точці  ;
; ;
; ;
; ;
; ;
; .
.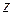 виражається функцією
виражається функцією  , де
, де  , а крива попиту для кожного товару
, а крива попиту для кожного товару  ,
,  , де
, де  . Знайти максимальний прибуток, який може бути досягнутий за цією умовою.
. Знайти максимальний прибуток, який може бути досягнутий за цією умовою. , умов. од.:
, умов. од.:
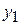 та
та  . Функція витрат має вигляд
. Функція витрат має вигляд  . Знайти такі значення
. Знайти такі значення 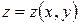 . Визначити витрати ресурсів
. Визначити витрати ресурсів  та
та  ;
;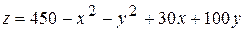 ;
; ;
; .
.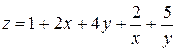 . При яких
. При яких 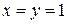 .
. потрібно та яка кількість сировини
потрібно та яка кількість сировини 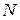 необхідно придбати фірмі для одержання найбільшого об’єму продукції
необхідно придбати фірмі для одержання найбільшого об’єму продукції  , якщо відомо, що об’єм прямо пропорційний до кількості робочих та кількості сировини з коефіцієнтом пропорційності рівним 10.
, якщо відомо, що об’єм прямо пропорційний до кількості робочих та кількості сировини з коефіцієнтом пропорційності рівним 10. . Ціна одиниці першого блага дорівнює 9, другого – 18. На придбання цих благ може бути затрачена сума, рівна 800. Як потрібно розподілити цю суму між двома благами, щоб користь від цих придбань була найбільшою.
. Ціна одиниці першого блага дорівнює 9, другого – 18. На придбання цих благ може бути затрачена сума, рівна 800. Як потрібно розподілити цю суму між двома благами, щоб користь від цих придбань була найбільшою. , а також функція кількості реалізованого товару
, а також функція кількості реалізованого товару  при встановленій ціні за одиницю, рівній
при встановленій ціні за одиницю, рівній  . Знайти оптимальні значення
. Знайти оптимальні значення 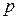 для монополіста-виробника у двох випадках:
для монополіста-виробника у двох випадках: ,
,  ;
; ,
,  .
.


