
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Обґрунтування рівноваги виробника на основі спільного аналізу виробничої функції та функції витрат.Содержание книги
Поиск на нашем сайте
Щоб з'ясувати, як впливають зміни співвідношення K/L на ефективність їх використання, слід ввести ряд понять, що характеризують результати виробництва: — сукупний продукт змінного фактора виробництва (у нашому випадку праці — TPL) — це кількість продукції, що виробляється при певній кількості цього фактора за інших незмінних умов;
— середній продукт, змінного фактора виробництва — граничний продукт змінного фактора Сукупний продукт змінного фактора зростає у міру того, як збільшуються затрати праці. Однак це зростання затухаюче. Більше того, настає момент, коли збільшення кількості праці не збільшує, а зменшує загальні результати виробництва. Це означає, що виробничий процес перенасичений працею, яка не може ефективно використовуватися за даного обсягу капіталу. У нашому прикладі це відбувається при співвідношенні K/L = 1/2. Зазначені залежності можна показати графічно. На рис. 5.5 показано криву сукупного продукту. Вона відображає, як змінюється випуск продукції при зміні одного з факторів виробництва, тоді як інші залишаються незмінними. Середній продукт змінного фактора можна визначити, якщо виміряти нахил променя, проведеного від початку координат через відповідну точку кривої сукупного продукту. Так, нахил променя ОА можна визначити через співвідношення координат точки А:
Середній продукт досягне свого максимуму за умови використання кількості праці, яка відповідає точці дотику променя, що виходить від початку координат, та кривої сукупного продукту. На рис. 5.5 це точка С. Якщо проведемо дотичні до кожної точки на кривій сукупного продукту та знайдемо тангенси кутів, що вони утворюють з віссю X, то отримаємо граничний продукт. Криві середнього та граничного продуктів подано на рис. 5.6. Середній продукт буде збільшуватися доти, поки граничний продукт буде більший за нього. Якщо до виробництва залучається нова порція ресурсу, продуктивність якої більша за середню, то таке залучення, звичайно, збільшить і середній показник. Навпаки, якщо гранична продуктивність змінного фактора виявиться менше середньої, то нове залучення зменшить середні показники. Тому свого максимального значення середній продукт змінного фактора досягатиме в точці перетину кривих середнього та граничного продуктів, тобто при АР = МР. У нашому прикладі ця точка лежить в інтервалі затрат праці від 50 до 60 люд.-год.
Економічні витрати залежать від кількості використаних ресурсів (їх затрат) та цін за послуги факторів виробництва. Тоді можна встановити залежність між обсягами виробництва та мінімально можливими витратами, необхідними для його отримання. Ця залежність називається функцією витрат:
де За допомогою функції витрат можна вирішувати як прямі, так і зворотні задачі: мінімізація витрат на заданий обсяг виробництва або максимізація виробництва при заданих витратах. Легко помітити зв'язок функції витрат з виробничою функцією, яка доповнюється урахуванням цін на відповідні виробничі ресурси. Загальні (сукупні) витрати (ТС) на виробництво можна розрахувати як суму витрат на придбання кожного фактора:
При фіксованих цінах на ресурси можна знайти різні набори капіталу та праці, які можна придбати за однакові витрати. Графічне зображення цих наборів називається ізокостою. Ізокоста — це лінія, що відображає затрати капіталу та праці, при яких витрати виробництва залишаються незмінними (рис. 6.1).
Кожен рівень затрат праці та капіталу має свою ізокосту. Нахил будь-якої ізокости із сімейства ізо кост дорівнює
Зміна ціни на працю чи капітал може змінити нахил ізокости (рис. 6.2): зростання ціни капіталу та зниження ціни праці збільшує кут нахилу; кут нахилу зменшується при зростанні ціни праці та зниженні ціни капіталу. Який же із запропонованих ізокостою наборів капіталу та праці забезпечить максимальний обсяг продукту? Щоб відповісти на це запитання, потрібно сумістити ізокости з картою ізоквант (рис. 6.3). Умовою для визначення максимальних обсягів виробництва при заданих витратах (як і мінімальних витрат на заданий обсяг виробництва) є однаковий нахил ізокости та відповідної ізокванти, що має спільну точку з ізокостою та найбільш віддалена від початку координат (точка А на рис. 6.3). Нахил ізокванти визначається граничною нормою технологічного заміщення, а ізокости — співвідношенням цін праці та капіталу. Тоді умову рівноваги
виробника, тобто такого його стану, в якому він не бажає змінювати співвідношення капіталу та праці, що задіяні у виробничому процесі, можна подати як рівність:
Оскільки
або
Рівняння (6.6) відображає принцип найменших витрат, суть якого у тому, що виробництво заданого обсягу продукції з мінімальними витратами вимагає, щоб ресурси, які одночасно використовуються, мали однакову величину граничного продукту на одиницю вартості ресурсу. Якщо граничний продукт на одиницю витрат одного фактора перевищує граничний продукт іншого фактора, то фірма може
отримати приріст продукції для реалізації без додаткових коштів за рахунок зміни співвідношення факторів виробництва. Якщо з'єднати точки, що відповідають комбінаціям факторів виробництва, які мінімізують витрати при різних заданих обсягах виробництва, то дістанемо так звану траєкторію зростання (рис. 6.4). Траєкторія зростання показує, як змінюється співвідношення факторів виробництва, що забезпечують мінімальні витрати, при збільшенні обсягів виробництва.
|
||||
|
Последнее изменение этой страницы: 2016-09-13; просмотров: 316; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.15.35.129 (0.009 с.) |


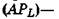 це відношення сукупного продукту
це відношення сукупного продукту Цей показник можна вважати продуктивністю змінного фактора;
Цей показник можна вважати продуктивністю змінного фактора; — це зміни за інших рівних умов сукупного продукту цього фактора при зміні кількості фактора на одиницю:
— це зміни за інших рівних умов сукупного продукту цього фактора при зміні кількості фактора на одиницю: 
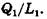 Це буде середній продукт у цій точці.
Це буде середній продукт у цій точці.

 І
І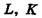 — затрати праці та капіталу; ціни відповідних ресурсів.
— затрати праці та капіталу; ціни відповідних ресурсів. 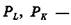


 Його можна виразити і через співвідношення цін:
Його можна виразити і через співвідношення цін:



 то справедливим
то справедливим





