
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Заміна змінної у визначеному інтеграліСодержание книги
Поиск на нашем сайте Нехай потрібно обчислити визначений інтеграл
Дійсно, за формулою Ньютона–Лейбніца
де
Враховуючи, що Приклад 5.30. Обчислити інтеграл Розв’язання. Замінимо
Зауваження. Варто звернути увагу на те, що при обчисленні визначеного інтеграла за допомогою заміни змінної немає необхідності повертатися до колишньої змінної.
Інтегрування частинами у визначеному інтегралі Нехай функції Проінтегрувавши рівність на відрізку
Оскільки
Приклад 5.31. Обчислити інтеграл Розв’язання. Нехай
Невласні інтеграли Вводячи визначений інтеграл як границю інтегральної суми, припускали, що відрізок інтегрування скінченний, а підінтегральна функція на ньому неперервна. Якщо хоча б одна з цих умов не виконується, дане визначення втрачає зміст, а визначений інтеграл називається невласним.
Невласні інтеграли з нескінченними границями інтегрування. Нехай функція
При
Якщо така границя існує і скінченна, інтеграл називається збіжним; якщо ж границя нескінченна чи не існує, то він розбіжний. Приклад 5.32. Обчислити інтеграл Розв’язання. Згідно (5.35) маємо
тобто інтеграл збігається. Як бачимо, результат залежить від поведінки первісної функції при Приклад 5.33. Обчислити інтеграл Розв’язання. Застосовуючи формулу (4.14), одержуємо
тобто інтеграл розбіжний. Аналогічно, якщо функція
може бути як збіжним, так і розбіжним. Приклад 5.34. Обчислити інтеграл Розв’язання. За означенням
Очевидно, що результат залежить від поведінки первісної при Для функції Невласні інтеграли мають властивості, аналогічні властивостям визначених інтегралів. Зокрема, якщо ввести умовні позначки
Невласні інтеграли від необмежених функцій. Нехай функція Тоді для будь-якого
Цей інтеграл може бути як збіжним, так і розбіжним, усе залежить від поведінки первісної при Приклад 5.35. Обчислити інтеграл Розв’язання. Підінтегральна функція
Даний інтеграл збіжний.
Геометричний зміст такого інтеграла для невід’ємної На рис. 5.5 показано геометричний зміст інтеграла
Аналогічно, можна ввести інтеграл
Якщо підінтегральна функція
Приклад 5.36. Обчислити інтеграл Розв’язання. Підінтегральна функція Внаслідок парності підінтегральної функції Отже, даний інтеграл розбіжний. Як і для невласних інтегралів з нескінченними межами, для кожного з невласних інтегралів від необмежених функцій є справедливою узагальнена формула Ньютона–Лейбніца.
|
||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 431; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.117.94 (0.006 с.) |

 , де функція
, де функція  неперервна на відрізку
неперервна на відрізку  . При цьому
. При цьому  диференційована функція на відрізку
диференційована функція на відрізку 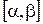 , причому
, причому  ,
,  . Покажемо, що
. Покажемо, що . (5.33)
. (5.33) ,
, – деяка первісна для функції
– деяка первісна для функції  є первісною для функції
є первісною для функції 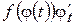 на відрізку
на відрізку  .
.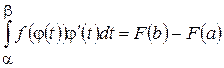 , тобто формула (5.33) вірна.
, тобто формула (5.33) вірна. .
. ,
,  . Якщо
. Якщо 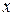 змінюється від 0 до 1, то змінна
змінюється від 0 до 1, то змінна  змінюється від 0 до
змінюється від 0 до  . Застосовуючи формулу (5.33) одержуємо
. Застосовуючи формулу (5.33) одержуємо

 і
і 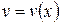 неперервні на відрізку
неперервні на відрізку 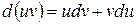 .
. .
. , то формула набуває вигляду
, то формула набуває вигляду  , звідки
, звідки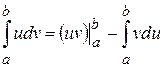 . (5.34)
. (5.34) .
. ,
,  . Тоді
. Тоді  ,
,  . Застосовуючи формулу (5.34), одержимо
. Застосовуючи формулу (5.34), одержимо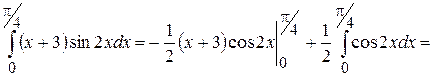
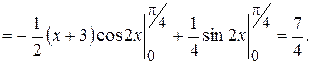
 . Тоді вона є неперервною на будь-якому відрізку
. Тоді вона є неперервною на будь-якому відрізку  .
. цей інтеграл є функцією своєї верхньої границі і тоді
цей інтеграл є функцією своєї верхньої границі і тоді . (5.35)
. (5.35) .
.
 Рис. 5.4.
Рис. 5.4.
 . Геометричний зміст такого інтеграла – для невід’ємної
. Геометричний зміст такого інтеграла – для невід’ємної  дорівнює площі смуги, що необмежена праворуч. На рис. 5.4 показано геометричний зміст інтеграла
дорівнює площі смуги, що необмежена праворуч. На рис. 5.4 показано геометричний зміст інтеграла  .
.
 , то
, то , (5.36)
, (5.36) .
.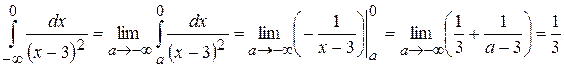 інтеграл збіжний.
інтеграл збіжний. .
.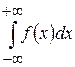 визначається рівністю
визначається рівністю 
 де
де 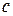 – будь-яке число. Якщо хоча б один з інтегралів правої частини рівності розбіжний, інтеграл
– будь-яке число. Якщо хоча б один з інтегралів правої частини рівності розбіжний, інтеграл 
 то одержимо для розглянутих інтегралів узагальнення формули Ньютона–Лейбніца:
то одержимо для розглянутих інтегралів узагальнення формули Ньютона–Лейбніца: ;
; ;
; .
. і необмежена поблизу
і необмежена поблизу 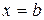 .
.
 існує і
існує і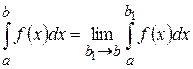 . (5.37)
. (5.37) .
. .
. визначена для всіх
визначена для всіх  , у точці
, у точці  функція
функція 
 Рис. 5.5.
Рис. 5.5.
 вісі
вісі  , ліворуч і праворуч прямими
, ліворуч і праворуч прямими  ,
,  .
. , де
, де  . (5.38)
. (5.38) , то
, то
 .
. розривна у точці
розривна у точці 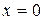 . Тому
. Тому  .
. , одержимо
, одержимо  .
.


