
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Додаткова вигода чи лишок виробника (продавця).Содержание книги
Поиск на нашем сайте
Для цього візьмемо криву пропозиції будь-якого товару
Рис. 5.22.
Так само, як деякі споживачі, завдяки дії ринкових сил, отримують можливість придбати товар за ціною нижче тієї, яку вони готові були заплатити, так і виробники іноді отримують можливість постачати товар на ринок за більш високою ціною, чим та, на яку вони згодні. Дійсно, крива пропозиції дає різні ціни, за якими виробники готові постачати на ринок відповідну кількість товарів. Так, за ціною
З іншого боку, кількість товару, яка менше чим
Знаходження капіталу (основних фондів) за відомими чистими інвестиціями. Нагадаємо, що чисті інвестиції (капіталовкладення) – це загальні інвестиції, які здійснюються в економіці протягом визначеного часу (частіше всього – року), без урахування інвестицій на відшкодування основних фондів (капіталу), що виходять з ладу. Таким чином, за одиницю часу капітал збільшується на величину чистих інвестицій. Якщо капітал позначити як функцію часу
тобто це похідна від капіталу за часом Часто потрібно визначити приріст капіталу за період часу з моменту часу
Зауважимо, що
Обернена задача для знаходження вартості ануїтету (регулярних платежів) щодо неперервних відсотків. У цьому випадку платежі залежать від часу, тобто є функцією від Потрібно визначити розмір вкладу
Рис. 5.23.
Якщо надходження неперервні, то протягом малого проміжку часу
За час
Щоб отримати загальний розмір вкладу
Ця наближена рівність стане точною, якщо проміжок часу
Раніше розглядали поняття дисконту, пов’язане для неперервних відсотків з формулою
Задача ануїтету в цьому випадку може бути сформульована так: знайти розмір початкового вкладу Розрахункова формула (її виведення аналогічне ануїтету з платежами) така:
де Наведемо декілька прикладів економічного змісту. Приклад 5.43. Відомо, що чисельність населення визначається за формулою Знайти необхідну кількість продукту для населення на проміжок часу Розв’язання. У малий проміжок часу кількість мешканців будемо вважати постійною, отже, на цей проміжок часу буде потрібна така кількість продукту:
Проінтегрувавши цю рівність на проміжку
Приклад 5.44. Відомо, що продуктивність праці робітника (кількість продукту, виготовленої за одиницю часу) протягом робочого дня змінюється. Нехай встановлена залежність між продуктивністю праці та часом, що виражається формулою Розв’язання. У малий проміжок часу, будемо вважати продуктивність праці постійною. Елементарна робота за час
Приклад 5.45. Визначити обсяг продукції, виготовленої робітником за другу годину робочого дня, якщо продуктивність праці характеризується функцією Розв’язання. Шуканий обсяг визначається за формулою
У нашому випадку
Приклад 5.46. Чисті інвестиції задані функцією
Визначити: а) приріст капіталу за три роки; б) через скільки років приріст капіталу ставитиме 50 000. Розв’язання. а) Скористаємося формулою для обчислення
б) Позначимо шуканий відрізок часу через
Підставимо
Нехай відомо функцію
Щодо функції зміни витрат часу на виготовлення виробів Приклад 5.47. Знайти середній час, витрачений на освоєння одного виробу в період освоєння від Розв’язання. Маємо
Приклад 5.48. Знайти середнє значення витрат Розв’язання. Відповідно до теореми про середнє значення
У нашому випадку
тобто середнє значення витрат дорівнює 16. Визначимо, при якому обсязі продукції витрати приймають це значення, тобто розв’яжемо рівняння
Враховуючи те, що обсяг продукції не може бути від'ємним, з останнього рівняння маємо
тобто При визначенні економічної ефективності капітальних вкладень зустрічаються задачі визначення початкової суми за її кінцевим значенням, отриманим через час Нехай Нехай доход, який надходить щорічно, змінюється в часі й описується функцією
Вправи 5.1–5.7. Використовуючи таблицю і властивості знайти невизначені інтеграли. 5.1. 5.3. 5.5. 5.7. 5.8–5.19. Знайти інтеграли. 5.8. 5.10. 5.12. 5.14. 5.16. 5.18. 5.20–5.31. Знайти інтеграли, застосовуючи метод інтегрування частинами. 5.20. 5.22. 5.24. 5.26. 5.28. 5.30. 5.32–5.40. Знайти інтеграл від дробу, у знаменнику якого квадратний тричлен. 5.32. 5.34. 5.36. 5.39. 5.41–5.49. Знайти інтеграли від раціональних дробів. 5.41. 5.43. 5.45. 5.47. 5.49. 5.50–5.55. Знайти інтеграли від тригонометричних функцій. 5.50. 5.52. 5.54. 5.56–5.60. Знайти інтеграли від ірраціональних функцій. 5.56. 5.58. 5.60. 5.61–5.67. Застосовуючи формулу Ньютона–Лейбніца, обчислити інтеграли.
5.61. 5.63. 5.65. 5.67. 5.68–5.73. Застосовуючи заміну змінної, обчислити інтеграли. 5.68. 5.70. 5.72. 5.74–5.76. Застосовуючи формулу інтегрування частинами обчислити визначені інтеграли. 5.74. 5.77–5.81. Обчислити невласні інтеграли 5.77. 5.80. 5.82. Обчислити площу фігури, обмеженої параболою 5.83. Обчислити площу фігури, обмеженої прямою 5.84. Знайти площу фігури, що розташована між лініями 5.85. Знайти площу фігури, що розташована між кривими 5.86. Знайти площу фігури, що обмежена кривою 5.87. Знайти площу фігури, що обмежена віссю 5.88. Знайти площу фігури, що обмежена астроїдою, заданою рівняннями 5.89. Обчислити площу фігури, що обмежена лемніскатою Бернуллі, заданою рівнянням 5.90. Обчислити площу однієї пелюстки трипелюсткової троянди 5.91. Обчислити довжину дуг кривих: а) б) 5.92. Знайти довжину однієї арки циклоїди (розташованої між двома нулями функції): 5.93. Обчислити довжину лінії, заданої в полярній системі координат: а) 5.94. Обчислити об'єм тіла, отриманого обертанням навколо вісі 5.95. Обчислити об'єм тіла, отриманого при обертанні навколо вісі 5.96. Обчислити об'єм тіла, отриманого при обертанні навколо осі 5.97. Визначити дисконтований прибуток за три роки при процентній ставці 8%, якщо первісні (базові) капіталовкладення становили 10 млрд грош. од. і намічається щорічно збільшувати капіталовкладення на 1 млрд грош. од. 5.98. За даними досліджень у розподілі доходів в одній із країн, крива Лоренца може бути описана рівнянням 5.99. Знайти середнє значення витрат 5.100. Продуктивність праці протягом робочого дня змінюється. Нехай функція продуктивності праці має вигляд 5.101. Через якийсь час після початку роботи продуктивність праці перестає рости і стає приблизно сталою. Визначити, скільки деталей зробить робітник за восьмигодинну зміну, якщо за перші дві години роботи продуктивність росте за законом
5.102. Знайти середнє значення витрат, якщо функція витрат задана рівнянням 5.103. Визначити дисконтований (початковий) обсяг прибутку, отриманого за 10 років, якщо щорічно прибуток дорівнює 100 тис. грош. од., процентна ставка – 5%. Відсотки нараховуються неперервно. 5.104. Витрата електроенергії, виробленої на електростанції, у період часу Визначити витрату електроенергії: а) за одну годину роботи, якщо б) за десяту годину роботи, якщо в) за п'яту годину роботи, якщо 5.105. Визначити кількість тракторів, випущених за п'ять років, якщо річний випуск зростав в арифметичній прогресії: 5.106. Функція граничного прибутку задається формулою
|
||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 229; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.193.255 (0.008 с.) |

 . Графік цієї кривої і точка рівноваги (перетину з кривою попиту) дані на рис. 5.22
. Графік цієї кривої і точка рівноваги (перетину з кривою попиту) дані на рис. 5.22
 (рис. 5.22) буде надано кількість товару
(рис. 5.22) буде надано кількість товару  . Припускаючи, що весь товар
. Припускаючи, що весь товар 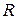
 .
. . Для обчислення площі цієї області, очевидно можна написати
. Для обчислення площі цієї області, очевидно можна написати .
. , а чисті інвестиції –
, а чисті інвестиції –  , сказане вище можна записати у вигляді
, сказане вище можна записати у вигляді ,
, .
. до
до  , тобто величину
, тобто величину .
. .
. .
. через
через 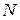 років. Для розв’язання розіб’ємо
років. Для розв’язання розіб’ємо  рівних проміжків часу
рівних проміжків часу 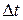 , як показано на рис. 5.23.
, як показано на рис. 5.23.
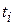 до
до  приблизно становитиме
приблизно становитиме .
. нарощувана сума, обчислена за формулою неперервних відсотків, за рахунок нарахування відсотків на внесок
нарощувана сума, обчислена за формулою неперервних відсотків, за рахунок нарахування відсотків на внесок 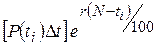 .
. .
. .
. .
. , якщо регулярні виплати за цим вкладом повинні становити
, якщо регулярні виплати за цим вкладом повинні становити  ,
, – неперервна процентна ставка.
– неперервна процентна ставка.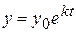 , де
, де 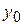 – число мешканців у початковий момент часу;
– число мешканців у початковий момент часу;  – коефіцієнт;
– коефіцієнт; 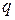 , тоді функція "споживання"
, тоді функція "споживання"  буде мати вигляд
буде мати вигляд  .
. .
.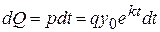 .
. , одержимо кількість продукту
, одержимо кількість продукту  , необхідну для населення на весь проміжок часу:
, необхідну для населення на весь проміжок часу: .
. , де
, де 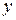 – продуктивність праці, що є функцією від часу. Визначити обсяг продукції, виготовленої робітником за останні дві години робочої зміни, тривалість якої
– продуктивність праці, що є функцією від часу. Визначити обсяг продукції, виготовленої робітником за останні дві години робочої зміни, тривалість якої 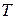 годин.
годин. буде
буде  . Звідси одержимо обсяг продукції, виготовленої робітником за останні дві години робочої зміни
. Звідси одержимо обсяг продукції, виготовленої робітником за останні дві години робочої зміни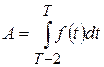 .
. .
. .
.
 .
.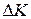 , поклавши
, поклавши  ,
,  :
:
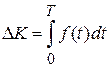 .
. і
і  ;
; ;
;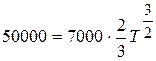 ;
; 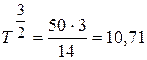 ;
;  (року).
(року).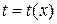 , що описує зміну витрат часу
, що описує зміну витрат часу  – порядковий номер виробу в партії. Тоді середній час
– порядковий номер виробу в партії. Тоді середній час  витрачений на виготовлення одного виробу в період освоєння від
витрачений на виготовлення одного виробу в період освоєння від  до
до  виробів, обчислюється за теоремою про середнє:
виробів, обчислюється за теоремою про середнє: .
. , то часто вона має вигляд
, то часто вона має вигляд  , де
, де  – витрати часу на виріб;
– витрати часу на виріб;  – показник виробничого процесу.
– показник виробничого процесу. до
до  виробів, якщо функція зміни витрат часу на виготовлення виробів
виробів, якщо функція зміни витрат часу на виготовлення виробів 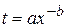 , де
, де  (хв),
(хв), 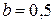 .
.
 , виражених у грошових одиницях, якщо обсяг продукції
, виражених у грошових одиницях, якщо обсяг продукції 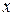 змінюється від 0 до 3 одиниць. Вказати обсяг продукції, при якому витрати приймають середнє значення.
змінюється від 0 до 3 одиниць. Вказати обсяг продукції, при якому витрати приймають середнє значення. .
.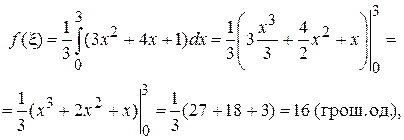
 або
або  .
. ,
, одиниць продукції.
одиниць продукції.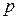 . Цей процес, як відомо, називається дисконтуванням.
. Цей процес, як відомо, називається дисконтуванням. – кінцева сума, отримана за
– кінцева сума, отримана за  – дисконтована (початкова) сума, яку у фінансовому аналізі називають також сучасною сумою. Якщо відсотки прості, то
– дисконтована (початкова) сума, яку у фінансовому аналізі називають також сучасною сумою. Якщо відсотки прості, то  , де
, де  – питома процентна ставка. Тоді
– питома процентна ставка. Тоді  . У випадку складних відсотків
. У випадку складних відсотків  і тому
і тому  . У випадку неперервного нарахування відсотків
. У випадку неперервного нарахування відсотків  і тому
і тому 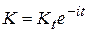 .
.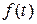 і при питомій нормі відсотка, рівній
і при питомій нормі відсотка, рівній  відсоток нараховується неперервно. Можна показати, що в цьому випадку дисконтований прибуток за період
відсоток нараховується неперервно. Можна показати, що в цьому випадку дисконтований прибуток за період  .
. . 5.2.
. 5.2.  .
. . 5.4.
. 5.4.  .
. . 5.6.
. 5.6.  .
. .
. . 5.9.
. 5.9.  .
. . 5.11.
. 5.11.  .
. . 5.13.
. 5.13. 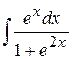 .
. . 5.15.
. 5.15.  .
. . 5.17.
. 5.17.  .
. . 5.19.
. 5.19.  .
. . 5.21.
. 5.21.  .
. . 5.23.
. 5.23.  .
. . 5.25.
. 5.25.  .
. . 5.27.
. 5.27.  .
. . 5.29.
. 5.29.  .
. . 5.31.
. 5.31. 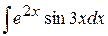 .
. . 5.33.
. 5.33. 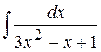 .
. . 5.35.
. 5.35.  .
. . 5.37.
. 5.37.  .
.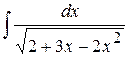 . 5.40.
. 5.40.  .
. . 5.42.
. 5.42.  .
. . 5.44.
. 5.44.  .
. . 5.46.
. 5.46.  .
. . 5.48.
. 5.48.  .
. .
. . 5.51.
. 5.51.  .
. . 5.53.
. 5.53.  .
. . 5.55.
. 5.55.  .
. . 5.57.
. 5.57.  .
.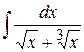 . 5.59.
. 5.59.  .
. .
. . 5.62.
. 5.62.  .
. . 5.64.
. 5.64.  .
. . 5.66.
. 5.66.  .
. .
. . 5.69.
. 5.69.  .
. . 5.71.
. 5.71.  .
. . 5.73.
. 5.73.  .
. . 5.75.
. 5.75.  . 5.76.
. 5.76.  .
. . 5.78.
. 5.78.  . 5.79.
. 5.79. 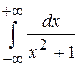 .
.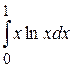 . 5.81.
. 5.81.  .
. і віссю
і віссю  .
. , параболою
, параболою  і віссю
і віссю  ,
,  ,
, 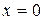 .
. і
і  .
.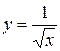 , віссю
, віссю  .
. ,
,  .
.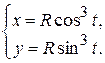
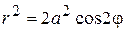 .
. .
. від
від 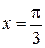 до
до  ;
; (астроїда).
(астроїда). ,
, 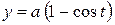 .
. ; б)
; б) 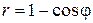 .
.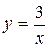 ,
,  .
. криволінійної трапеції, обмеженої лініями
криволінійної трапеції, обмеженої лініями  ,
,  .
. , де
, де  , виражених у грошових одиницях, якщо обсяг продукції
, виражених у грошових одиницях, якщо обсяг продукції 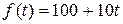 (деталей/рік). Скільки деталей зробить робітник за весь час роботи? (Тут
(деталей/рік). Скільки деталей зробить робітник за весь час роботи? (Тут 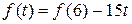 , де
, де  – продуктивність праці наприкінці шостої години роботи. Визначити середню продуктивність праці за зміну.
– продуктивність праці наприкінці шостої години роботи. Визначити середню продуктивність праці за зміну. (
( , де
, де  – навантаження на електростанцію, кВт/год;
– навантаження на електростанцію, кВт/год;  ;
; ;
;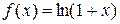 .
. , де
, де  , де
, де 


