
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Інтегрування трансцендентних функцій.Содержание книги
Поиск на нашем сайте
Інтеграли виду
де
Ця підстановка перетворює інтеграл (5.16) до виду
Помітимо, що підстановка (5.16) часто призводить до громіздких викладок, тому її використовують тоді, коли не знайдено інших шляхів інтегрування. Якщо підінтегральна функція має одну із властивостей 1) 2) 3) то для обчислення інтегралу зручно використовувати підстановки 1) 3) Приклад 5.27. Обчислити інтеграл Розв’язання. Тут
Інтеграли виду
де Інтеграли виду
підстановками Зауважимо, що при досить великих степенях зручно застосовувати формули зниження (одержані інтегруванням частинами):
Інтеграли виду
обчислюються після перетворення добутку тригонометричних функцій в алгебраїчну суму за допомогою формул тригонометрії:
Приклад 5.28. Обчислити Розв’язання. Використаємо тригонометричні формули:
Тоді
Інтеграли виду
де Зауважимо, що має місце формула Ейлера
яку можна використати для контролю при обчисленні відповідних інтегралів. Інтеграли від трансцендентних функцій часто не виражаються через елементарні функції. До таких інтегралів відносяться, наприклад, такі, які часто зустрічаються:
Первісні (5.22), які при
Поняття визначеного інтегралу Нехай функція
який назвемо інтегральною сумою. Означення 5.3. Якщо існує скінчена границя
функцію Означення 5.4. Нижньою та верхньою сумами Дарбу функції
де Теорема 5.2. Для того, щоб функція
де Зокрема неперервна функція, кусочно-неперервна функція і монотонна на сегменті інтегровані на ньому.
Геометричний зміст визначеного інтеграла Нехай у площині
Розіб'ємо відрізок Площу криволінійної трапеції з основою
За площу криволінійної трапеції природно прийняти границю, до якої прагнуть площі побудованих зазначеним способом східчастих фігур при наближенні до нуля відрізків
Виходячи з формули (5.28) та означення визначеного інтегралу можна стверджувати, що
|
|||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 279; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.12.34.96 (0.008 с.) |

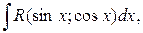 (5.15)
(5.15) раціональна функція змінних
раціональна функція змінних 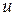 і
і  завжди можна звести до інтегралів від раціональних функцій за допомогою підстановки (її називають універсальною тригонометричною підстановкою)
завжди можна звести до інтегралів від раціональних функцій за допомогою підстановки (її називають універсальною тригонометричною підстановкою)
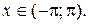 (5.16)
(5.16)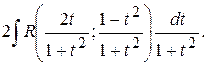 (5.17)
(5.17)



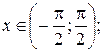 2)
2) 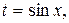




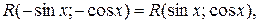 тому, поклавши
тому, поклавши  одержимо
одержимо

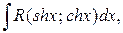 (5.18)
(5.18) , завжди можна звести до інтегралів від раціональних функцій
, завжди можна звести до інтегралів від раціональних функцій 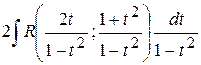 з допомогою підстановки
з допомогою підстановки  Іноді зручно використовувати підстановки
Іноді зручно використовувати підстановки 



 (5.19)
(5.19)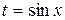 або
або  і відповідно
і відповідно  або
або 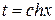 завжди можна звести до інтегралів від диференціального бінома.
завжди можна звести до інтегралів від диференціального бінома.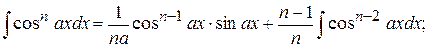
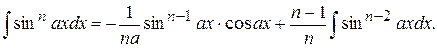


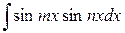 (5.20)
(5.20)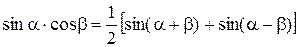 ;
;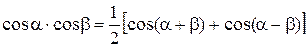 ;
; .
. .
.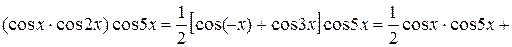




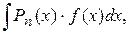 (5.21)
(5.21) многочлен степеня
многочлен степеня 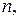 а
а  одна з наступних функцій:
одна з наступних функцій: 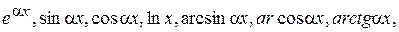
 обчислюються за допомогою багатократного інтегрування частинами.
обчислюються за допомогою багатократного інтегрування частинами.
 ;
; 
 ; (5.22)
; (5.22)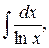
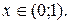 (5.23)
(5.23) перетворюються в нуль, позначаються відповідно
перетворюються в нуль, позначаються відповідно 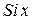 (інтегральний синус) та
(інтегральний синус) та 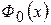 (інтеграл ймовірностей). Первісна (5.23), яка прямує до нуля при
(інтеграл ймовірностей). Первісна (5.23), яка прямує до нуля при  позначається
позначається  та називається інтегральним логарифмом.
та називається інтегральним логарифмом. визначена на сегменті
визначена на сегменті  і
і  довільне розбиття цього сегменту на
довільне розбиття цього сегменту на  частин. Позначимо
частин. Позначимо 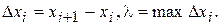 Виберемо на кожному із сегментів точку
Виберемо на кожному із сегментів точку  і складемо вираз
і складемо вираз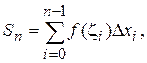 (5.24)
(5.24)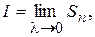 яка не залежить від способу розбиття сегмента
яка не залежить від способу розбиття сегмента  то число
то число  називають означеним інтегралом функції
називають означеним інтегралом функції  (5.25)
(5.25)
 (5.26)
(5.26)

 необхідно і достатньо, щоб виконувалась рівність
необхідно і достатньо, щоб виконувалась рівність (5.27)
(5.27) коливання функції
коливання функції  .
. дана фігура, обмежена відрізком
дана фігура, обмежена відрізком  вісі
вісі  , прямими
, прямими  ,
, 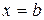 і кривою
і кривою  , де
, де  – неперервна, невід’ємна на відрізку
– неперервна, невід’ємна на відрізку  цієї трапеції.
цієї трапеції. Рис. 5.1.
Рис. 5.1.
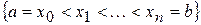 . Через точки поділу проведемо прямі
. Через точки поділу проведемо прямі  ,
, 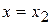 , …,
, …, 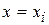 , …,
, …, 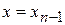 , розбиваючи криволінійну трапецію на
, розбиваючи криволінійну трапецію на 
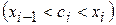 і побудуємо прямокутники з основою
і побудуємо прямокутники з основою  і висотою
і висотою 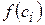 . Площу кожної трапеції з основою
. Площу кожної трапеції з основою 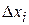 обчислимо наближено, як площу прямокутника з такою же основою і висотою
обчислимо наближено, як площу прямокутника з такою же основою і висотою 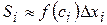 .
.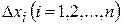 , одержимо
, одержимо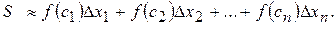
 . (5.28)
. (5.28) дорівнює площі криволінійної трапеції, обмеженої відрізком
дорівнює площі криволінійної трапеції, обмеженої відрізком 


