
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Знайдіть похідну функції в точці x, використовуючи означення похідної.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
а) б) в) г) д) 2. Скласти рівняння дотичної і нормалі до кривої 3. Скласти рівняння дотичної і нормалі до параболи 4. Написати рівняння дотичної і нормалі до функції а) б) 5. У якій точці дотична до кривої 6. Під яким кутом дотична до кривої 7. У параболи а) (0;0); б) (2;1); в) (4;0). Знайти величину кута нахилу до дотичної до осі Ох.
Геометричне застосування похідної Рівняння дотичної до графіка функції
а рівняння нормалі
Довжина дотичної
довжина нормалі
довжина піддотичної
довжина піднормалі
Правило обчислення похідних. Похідна показникової, логарифмічної, тригонометричної, складеної функцій. Основні правила диференціонування. Вважаємо, що 1. 2. 3. 4. 5. Якщо 6. Якщо 7. Якщо Таблиця похідних. 1. 3. 5. 7. 10. 18. I. Знайдіть похідні наступних функції: 1. 3. 5. 7. 9. 11. 13. 15. II. Знайдіть похідну функції в т.
Монотонність функції. Локальний екстремум функції. Найбільше і найменше значення функції. Монотонність і екстремум функції
Якщо Якщо функція У випадку мінімуму похідна, проходячи через цю точку зліва направо, змінює знак з «-» на «+», у випадку максимуму – з «+» на «-». Функція Якщо в точці
порядку, то в цій точці функція має екстремум, при чому мінімум, якщо ця похідна додатна, і максимум, якщо від’ємна.
Найбільше і найменше значення функції Неперервна на відрізку
I.Знайти і обчислити інтервали монотонності функції: 1. 2. 3. 4. 5. 6. 7. II.Знайти локальні екстремуми функцій:
III. Знайти найбільше і найменше значення функції на заданому відрізку:
IV.Використовуючи другу умову локального екстремуму, знайти локальні екстремуми функції:
V. Використовуючи третю достатню умову локального екстремуму, знайти локальні екстремуми функції в т. 1. 2. Опуклість і вгнутість кривих. Точки перегину. Асимптоти кривої. Дослідження функції та побудова її графіка Опуклість і вгнутість кривих Якщо
Асимптоти кривої Вертикальна асимптота графіка функції
де
де
якщо ці границі існують і скінчені.
Схема дослідження функції та побудова її графіка Схема дослідження: 1) знайти область існування функції; 2) знайти (якщо це можливо) точки перетину графіка з координатними осями; 3) дослідити функцію на періодичність, парність і непарність; 4) знайти точки розриву та дослідити їх; 5) знайти інтервали монотонності, точки екстремумів та значення функції у цих точках;знайти інтервали опуклості, вгнутості та точки перегину; 6) знайти асимптоти графіка функції; 7) на основі проведеного дослідженння побудувати графік функції. І. Дослідити на опуклість графіки функцій: 1. 2. 3. 4. 5. 6.
ІІ. Знайти точки перегину графіка функції: 1. 2. 3. 4. 5. 6.
ІІІ. Знайти асимптоти кривих: 1. 2. 3. 4. 5. ІV. Дослідити функцію і побудувати її графік:
1. 2. 3. 4. 5.
Глава 5. Інтегральне числення функції однієї змінної
Невизначений інтеграл. Основні методи інтегрування невизначеного інтеграла
|
|||||
|
Последнее изменение этой страницы: 2016-06-23; просмотров: 441; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.217.156.67 (0.009 с.) |

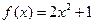 ;
; ;
; ;
; ;
; .
.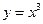 в т. А(2;8). Знайти довжини відрізків дотичної і нормалі в цій точці.
в т. А(2;8). Знайти довжини відрізків дотичної і нормалі в цій точці. в т. (2;4). Знайти довжини піддотичної і піднормалі в цій точці.
в т. (2;4). Знайти довжини піддотичної і піднормалі в цій точці.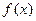 в точці
в точці  :
: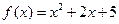 ; т.
; т.  ;
; ; т.
; т.  нахилена до осі Ох під кутом, величина якого дорівнює
нахилена до осі Ох під кутом, величина якого дорівнює  ?
? в точці (0;1) перетинає вісь Ох?
в точці (0;1) перетинає вісь Ох? проведена дотична в точці:
проведена дотична в точці: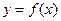 у точці
у точці  має вигляд
має вигляд ,
, .
. ;
; ;
; ;
; .
. - стала величина, а
- стала величина, а  і
і  - деякі диференційовні функції від
- деякі диференційовні функції від  .
. .
. .
. .
. .
. , де
, де  , або
, або  .
. , то
, то  .
. , то
, то  .
. . 2.
. 2. 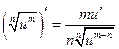 .
. . 4.
. 4.  .
. . 6.
. 6.  .
. . 8.
. 8.  . 9.
. 9.  .
. . 11.
. 11.  . 12.
. 12.  . 13.
. 13.  . 14.
. 14.  . 15.
. 15.  . 16.
. 16.  . 17.
. 17.  .
. .
. ; 2.
; 2. 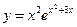 ;
; ; 4.
; 4.  ;
; ; 6.
; 6.  ;
; ; 8.
; 8.  ;
; ; 10.
; 10.  ;
; ; 12.
; 12.  ;
; ; 14.
; 14. 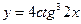 ;
; .
. ,
, 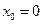 ;
; ,
,  ,
,  ,
,  ;
; ,
,  ;
; ,
,  ;
; ,
,  .
. для
для  , то функція
, то функція  і
і  .
.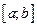 функція
функція  ;
; ;
; ;
; ;
; ;
; ;
; .
. ;
; ;
; ;
; ;
; .
. ,
,  ;
; ,
,  .
. ;
; ;
; ;
; ;
;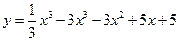 .
. ; т.
; т.  ;
; ; т.
; т.  .
. ,
,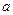 - те значення аргументу, при якому функція
- те значення аргументу, при якому функція  ,
, ,
,  ,
, ;
; ;
; ;
; ;
; ;
; .
. ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
;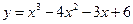 ;
; ;
;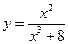 .
.


