
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лекція №8 Похідні вищих порядків. Формула Тейлора.Содержание книги
Поиск на нашем сайте
1. Похідні вищих порядків. Означення. Приклади в Нехай Означення. Похідним відображенням порядку Для конкретизації цього означення може бути вдало використано поняття похідної за направленням. При при
отже Крім того, з означення похідної у напрямку, матимемо
Аналогічно,
Приклад.
Для будь-яких
Отже Аналогічно
Крім того, нижче будемо називати диференціалом k-го ґатунку в точці х відображення
де 2. Симетричність похідної вищого порядку Теорема. Якщо для Доведення. Скористаємось методом математичної індукції. Перевіримо справедливість для
Оскільки Скориставшись цими зауваженнями і наслідком теореми про скінчений приріст, матимемо:
і
Тоді матимемо
Припустимо, що при У випадку відображення Означення. Відображення Нехай Нижче нам знадобиться наступний приклад. Приклад. –
Отже 3. Формула Тейлора. Приклади в Теорема. Якщо відображення
Доведення. Покажемо справедливість формули по індукції. При
Тоді за формулою скінчених приростів
Приклади. 1. 2.
Практичне заняття №12 Тема: Похідна та диференціал вищого порядку. Формула Тейлора. Основні відомості: 1. Означення похідної та диференціала вищого порядку. Приклади в 2. Теорема про симетричність похідної k-го порядку. 3. Формула Тейлора.
Задачі: 1.1. 1.2. 1.3. Знайти 1.4. 2.1. 2.2. 2.3. 3.1. 3.2. Знайти кілька перших членів розкладу функції 3.3.Розкласти за формулою Тейлора в точці (0,0) функції а). б) Завдання для самостійної роботи
1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. Розкласти за степенями 14. Розкласти 15. Розкласти по формулі Тейлора у точці (0,0) 16. 17. 18. 19. 20. 21. 23.
|
||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 316; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.45.82 (0.007 с.) |


 – нормовані, повні простори і f – диференційоване і
– нормовані, повні простори і f – диференційоване і  . Якщо
. Якщо  означена в деякому околі х і диференційоване відображення, то його похідне відображення
означена в деякому околі х і диференційоване відображення, то його похідне відображення  називається другим похідним відображенням і позначається
називається другим похідним відображенням і позначається  .
. відображення
відображення  у точці
у точці  називається похідна в цій точці до похідного відображення порядку
називається похідна в цій точці до похідного відображення порядку  від f.
від f. 
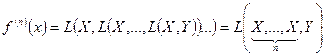 , тобто
, тобто  можна інтерпретувати як
можна інтерпретувати як  - лінійний неперервний оператор.
- лінійний неперервний оператор.
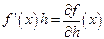 в розумінні означення, раніше зазначеного;
в розумінні означення, раніше зазначеного;
 , то фіксуючи
, то фіксуючи  , а обчисливши значення оператора на
, а обчисливши значення оператора на 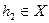 матимемо
матимемо ,
, , тому
, тому  .
. , тобто
, тобто  .
.




 ,
,  .
. ,
, 

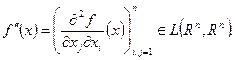


 Для будь-якого k будемо мати
Для будь-якого k будемо мати вираз
вираз  , де
, де  довільний вектор
довільний вектор  . У випадку нашого прикладу,
. У випадку нашого прикладу,  , маємо
, маємо ,
, .
.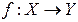 форма
форма  не залежить від порядку
не залежить від порядку  .
. . Нехай
. Нехай  і
і  фіксовані вектори з Х. Розглянемо функцію від
фіксовані вектори з Х. Розглянемо функцію від 

 .
. , визначену для векторів
, визначену для векторів  і таких, що
і таких, що  . Тоді
. Тоді  .
. має в точці х другий диференціал, то існує окіл точки х, у якому f диференційована. Будемо вважати t настільки малим, що аргументи в правій частині в F належать цьому околу точки х.
має в точці х другий диференціал, то існує окіл точки х, у якому f диференційована. Будемо вважати t настільки малим, що аргументи в правій частині в F належать цьому околу точки х.

 ,
, .
. . Це означає, що
. Це означає, що  . Оскільки
. Оскільки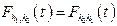 , то
, то  .
.
 , тоді при
, тоді при 
 (ми скористалися припущенням симетричності похідної k-го ґатунку), що і треба було довести.
(ми скористалися припущенням симетричності похідної k-го ґатунку), що і треба було довести. , з урахуванням достатньої умови диференційованості функції (див. лекцію 7), та вигляду
, з урахуванням достатньої умови диференційованості функції (див. лекцію 7), та вигляду  розглянемо означення.
розглянемо означення. , якщо у деякім околі точки х вона має всі частинні похідні k-го ґатунку неперервні у самій точці х.
, якщо у деякім околі точки х вона має всі частинні похідні k-го ґатунку неперервні у самій точці х. не залежать від порядку диференціювання, так як
не залежать від порядку диференціювання, так як – базис в
– базис в  .
. , А – симетричне.
, А – симетричне. 
 ,
, 
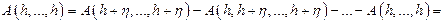

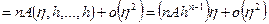 .
. .
. і
і  околу
околу  точки х нормованого простору Х в нормований простір
точки х нормованого простору Х в нормований простір  таке, що f має в
таке, що f має в 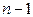 включно, а в самій точці х має похідну
включно, а в самій точці х має похідну  порядку
порядку  , то
, то при
при  .
. вона вірна в силу означення
вона вірна в силу означення  . Нехай формула вірна при
. Нехай формула вірна при  . Тоді покажемо справедливість для
. Тоді покажемо справедливість для  . Розглянемо
. Розглянемо , визначену в околі
, визначену в околі  зі значеннями в
зі значеннями в 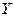 , яка диференційована (в силу розглянутого прикладу). Тоді
, яка диференційована (в силу розглянутого прикладу). Тоді . Застосуємо до
. Застосуємо до  формулу з теореми при
формулу з теореми при  , для функції
, для функції  , тобто
, тобто

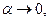 при
при  .
. , що і дає шуканий результат.
, що і дає шуканий результат.
 .
. ,
, 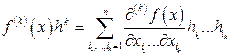

 та
та  .
. ,
,  . Знайти
. Знайти  ,
,  .
. . Показати, що
. Показати, що  =
= 
 ,
,  . Якщо
. Якщо  .
.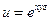 ,
,  .
. . Знайти
. Знайти  .
. . Знайти
. Знайти  у точці
у точці  .
. . Знайти
. Знайти  .
. . Розкласти
. Розкласти  по степеням
по степеням  .
. по формулі Тейлора в точці (0,0).
по формулі Тейлора в точці (0,0).

 . Довести
. Довести  . Довести
. Довести 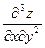 =
= 
 . Довести
. Довести  =
=  =
=  .
. .
. . Знайти
. Знайти  .
. . Знайти
. Знайти  . Знайти
. Знайти  .
. .
.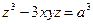 . Знайти
. Знайти  . Знайти
. Знайти 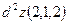 .
.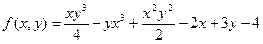 . Обчислити
. Обчислити  , обмежившись членами до другого порядку включно.
, обмежившись членами до другого порядку включно. функцію
функцію  ,
,  .
.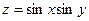 по степенях
по степенях 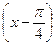 і
і  до другого порядку включно.
до другого порядку включно. розкласти по степенях
розкласти по степенях 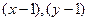 до третього порядку включно, та обчислити
до третього порядку включно, та обчислити  .
.
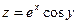


 ,
,  . Знайти
. Знайти  .
. . Знайти
. Знайти  .
. ,
, 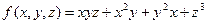 . Знайти
. Знайти  .
.


