
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Задачі для самостійного розв’язку.Содержание книги
Поиск на нашем сайте
Нехай Х- лінійний простір зі скалярним добутком. 1. Два вектори 2. Показати, що знак рівності в нерівності Коші-Буняковського має місце тоді і тільки тоді, коли 3. Довести, що 4. Довести формулу
5. Обчислити норму оператора а). б). в). 6. Довести, що оператор 7. Якщо 8. Нехай Лекція №4 Похідна у напрямку. Частинні похідні. Повна похідна. 1. Похідна у напрямку. Розглянемо Якщо покласти Якщо F скінчено вимірний, то у ньому можна вибрати систему координат, тоді Приклад.
Теорема. Для того, щоб функція із значеннями у скінчено вимірному нормованому просторі була диференційована, необхідно і достатньо, щоб її компоненти у деякій системі координат були скалярними диференційованими функціями. Компоненти похідної – похідні відповідних компонент. Нехай Означення. Нехай Якщо Якщо Якщо Y – скінчено вимірний і
Припустимо, що Х – скінчено вимірний і Приклад.
Якщо Х і Y – скінчено вимірні з системами координат Нижче матрицю Якщо При Приклади. 1. 2. Матриця Якобі 2. Повна похідна Означення. Нехай Означення. Лінійна відносно h функція Теорема. Якщо відображення Доведення. Нехай
тобто f має похідну в точці х у будь-якому напрямку, і Покажемо, що похідна єдина. Якщо Неперервність f у точці х випливає з рівності Нехай Зауважимо, що в силу означення диференційованості випливає, що відображення, диференційоване в точці – неперервне у цій точці. Обернене невірне, наприклад, функція Зауваження. Умову диференційованості у точці Приклади. 1.
2. Якщо
3. Нехай
У координатній формі запису
Отже 4. Якщо
Якщо Але обернене твердження невірне. Наприклад:
Але в (0,0) функція не неперервна, значить і не диференційована.
|
||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 236; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.221.161.43 (0.008 с.) |

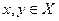 ортогональні, якщо
ортогональні, якщо  . Довести, що якщо
. Довести, що якщо 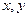 ортогональні, то
ортогональні, то  (теорема Піфагора)
(теорема Піфагора) .
. виконується рівність паралелограма
виконується рівність паралелограма 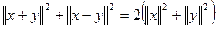 .
. , для
, для 
 , якщо
, якщо 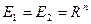 з нормами:
з нормами: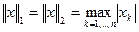

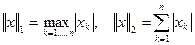
 - неперервний, де
- неперервний, де  , а
, а  .
.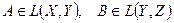 , то
, то 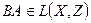 та
та  .
.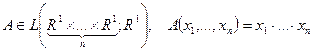 .Довести, що
.Довести, що  .
.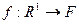 , F – нормований простір, для
, F – нормований простір, для  можна надати змісту формі
можна надати змісту формі 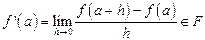 , де границя у розумінні нормованого простору F.
, де границя у розумінні нормованого простору F. , то отримаємо звичайну похідну дійсної функції дійсної змінної.
, то отримаємо звичайну похідну дійсної функції дійсної змінної.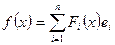
 – базис,
– базис,  , при цьому
, при цьому  .
.
 .
.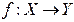 , де
, де 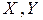 – нормовані простори. Говорити про похідну у попередньому розумінні немає можливості. Тому розглянемо поняття частинної похідної вздовж вектора
– нормовані простори. Говорити про похідну у попередньому розумінні немає можливості. Тому розглянемо поняття частинної похідної вздовж вектора  .
. . Похідною функції f в х вздовж вектора
. Похідною функції f в х вздовж вектора 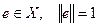 називається похідна, якщо вона існує, функції
називається похідна, якщо вона існує, функції 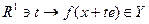 при
при  ,
,  .
.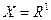 і
і 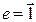 , то похідна вздовж е є звичайною похідною у розумінні першого означення
, то похідна вздовж е є звичайною похідною у розумінні першого означення  .
. існує для усіх х, то можна розглядати функцію
існує для усіх х, то можна розглядати функцію  .
. – базис в Y, то має місце формула
– базис в Y, то має місце формула 
 . З означення похідної у напрямку
. З означення похідної у напрямку 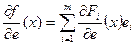 .
. – базис в Х. Тоді похідні у напрямку векторів
– базис в Х. Тоді похідні у напрямку векторів 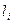 зазвичай називають частинними похідними f, тобто
зазвичай називають частинними похідними f, тобто 
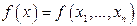
 .
. .
. і
і  .
.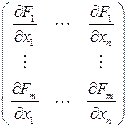 будемо називати матрицею Якобі f у точці х.
будемо називати матрицею Якобі f у точці х. , то визначник матриці називається визначником Якобі (Якобіан) і позначається
, то визначник матриці називається визначником Якобі (Якобіан) і позначається  .
. він спрощується до звичайної похідної.
він спрощується до звичайної похідної.
 .
.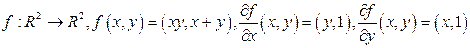
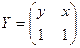 .
.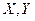 – нормовані простори. Відображення
– нормовані простори. Відображення  називається диференційованим у точці
називається диференційованим у точці  , якщо існує таке лінійне неперервне відображення
, якщо існує таке лінійне неперервне відображення  що
що  , де
, де  при
при  , тобто
, тобто  .
. називається дотичним відображенням або похідною відображення
називається дотичним відображенням або похідною відображення  в точці х. Позначення:
в точці х. Позначення:  .
. , то його похідна єдина. У цьому випадку f неперервне в х. Крім того, у точці х відображення f має похідну вздовж будь-якого напрямку
, то його похідна єдина. У цьому випадку f неперервне в х. Крім того, у точці х відображення f має похідну вздовж будь-якого напрямку  , а відображення
, а відображення 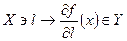 лінійне неперервне відображення
лінійне неперервне відображення  і
і  .
.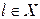 , покладаючи в означенні похідної
, покладаючи в означенні похідної  маємо
маємо  , або
, або 

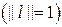 , при
, при  отримаємо, що
отримаємо, що  ,
, неперервне і лінійне по l.
неперервне і лінійне по l. і
і 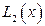 – похідні f, то
– похідні f, то  ,
,  , тобто
, тобто  .
. , тобто маємо
, тобто маємо  .
. диференційована в кожній точці
диференційована в кожній точці  , тобто диференційована на Х, то виникає функція
, тобто диференційована на Х, то виникає функція  , яку називають похідною від f або похідним відображенням. Значення
, яку називають похідною від f або похідним відображенням. Значення 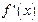 в точці
в точці  , яка є диференціалом або похідною функції f у даній конкретній точці
, яка є диференціалом або похідною функції f у даній конкретній точці 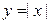 в точці х =0 неперервна, але не диференційована.
в точці х =0 неперервна, але не диференційована. можна записати так:
можна записати так: 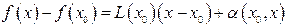 ,
,  при
при  . Зрозуміло, що означення насправді відноситься до відображень
. Зрозуміло, що означення насправді відноситься до відображень  будь-яких афінних просторів
будь-яких афінних просторів  , лінійні простори Х і Y яких нормовані.
, лінійні простори Х і Y яких нормовані.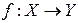 , Х – скінчено вимірна зі скалярним добутком,
, Х – скінчено вимірна зі скалярним добутком,  де
де 
 то
то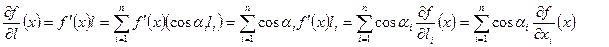
 , то для будь-якого напрямку
, то для будь-якого напрямку 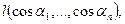
 Отже
Отже 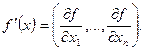
 , де
, де  і
і  відповідно.
відповідно. , маємо, для будь-якого
, маємо, для будь-якого  .
.
 (у координатній формі запису).
(у координатній формі запису).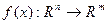 , то
, то  Отже, з приклада 3 маємо
Отже, з приклада 3 маємо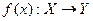 і існує
і існує  у деякій точці х, то існують
у деякій точці х, то існують  (х), тобто існує матриця Якобі у х.
(х), тобто існує матриця Якобі у х.




