
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Нерівність Коші-Буняковського .Содержание книги
Поиск на нашем сайте Для будь-яких
Нерівність та слідуючу теорему довести у якості вправ. Теорема. Якщо у векторному просторі Х заданий скалярний добуток, то функція
Скінченовимірний простір Х з скалярним добутком називається Евклідовим простором. Нескінченновимірний повний простір Х зі скалярним добутком – Гільбертовий простір.
2. Лінійні оператори. Означення. Нехай Х і Y – векторні простори. Відображення
Означення. Відображення При n=1 А – лінійне відображення; при n=2 А – білінійне відображення.
Якщо
Приклади. 1. 2. 3. Скалярний добуток у векторному просторі 4. Нехай 5. Нехай
6.
3. Простори неперервних лінійних операторів. Норма оператора Нехай Означення. Полілінійний оператор називається обмеженим на
Число Очевидно, що
Із властивостей лінійності
(
У випадку Приклади. 1. 2. Нехай у Х визначен скалярний добуток 3.
З іншого боку
тобто 4. 5. 6. Якщо Довести приклади 4, 5, 6 у якості вправ. Теорема. Для лінійного оператора 1. А – має скінчену норму; 2. А – обмежений оператор; 3. А – неперервний оператор; 4. А – неперервний в Доведення. Еквівалентність 1 і 2 очевидна. Доведемо еквівалентність 1, 2 і 3. Нехай А – обмежений, тобто Навпаки, нехай справедлива умова 3, тобто А – неперервне в Х. Покажемо, що А – обмежений. Нехай А необмежений, тобто існує Покажемо еквівалентність умов 3 і 4. Із умови 3 слідує умова 4. Доведемо, що з умови 4 слідує умова 3. Нехай А неперервний в 0. Якщо Зауваження. Аналогічне твердження справедливе коли А полілінійне відображення Теорема. Норма полілінійного оператора є нормою в лінійному просторі Доведення. Властивості норми легко довести з означення норми полінійного оператора. Покажемо, що L повний при умові, що Y повний. Нехай
Тоді
Перейдемо до границі при Легко довести слідуче твердження. Теорема. Якщо
Теорема. Між простором Доведення. Нехай,
. З означення оператора А випливає взаємно-однозначність відображення. Наслідок. Практичне заняття №8 Тема: Лінійний нормований простір зі скалярним добутком. Лінійні оператори. Основні відомості: 1. Означення скалярного добутку. 2. Означення та властивості лінійного, полілінійного операторів. Обмеженого оператора. Задачі Нехай Х – лінійний простір зі скалярним добутком. 1.1.Довести властивості скалярного добутку: 1. 2. 1.2. Довести нерівність Коші-Буняковського
1.3. Довести нерівність трикутника
для норми асоційованої зі скалярним добутком 1.4. Нехай Х скінчено вимірний лінійний простір зі скалярним добутком. Довести, що існує ортонормований базис у Х. Якщо 2.1. Нехай 2.2. Якщо 2.3. Якщо 2.4. Нехай
|
||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 497; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.219.108.149 (0.009 с.) |

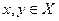
 .
. є нормою асоційованою з скалярним добутком в Х.
є нормою асоційованою з скалярним добутком в Х. – лінійне, якщо
– лінійне, якщо  і
і  1 виконуються рівності:
1 виконуються рівності: ,
, .
. прямого добутку лінійних просторів
прямого добутку лінійних просторів 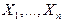 в лінійний простір Y називається полілінійним (n-лінійним) якщо це відображення
в лінійний простір Y називається полілінійним (n-лінійним) якщо це відображення  лінійне по кожній змінній при фіксованих значеннях інших змінних.
лінійне по кожній змінній при фіксованих значеннях інших змінних. – множина n-лінійних відображень.
– множина n-лінійних відображень. , то лінійне і полілінійне відображення називаються функціоналами і полілінійними функціоналами.
, то лінійне і полілінійне відображення називаються функціоналами і полілінійними функціоналами. – лінійний простір числових фінітних послідовностей
– лінійний простір числових фінітних послідовностей  ,
,  - лінійний оператор.
- лінійний оператор.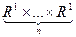 , А
, А  – n-лінійна функція
– n-лінійна функція 
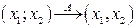 – білінійна функція.
– білінійна функція. – лінійне в Х. Якщо
– лінійне в Х. Якщо 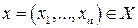 , то
, то 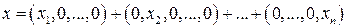 ,
,  ,
,  ,
,  – лінійне відображення і
– лінійне відображення і  – загальний вигляд,
– загальний вигляд,  .
. лінійне в Х, тоді
лінійне в Х, тоді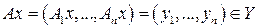 ,
,  – лінійні.
– лінійні. ,
, 
 – лінійне відображення. Якщо
– лінійне відображення. Якщо  , то
, то  – лінійне відображення, тобто
– лінійне відображення, тобто  – одержуємо знайомий числовий запис лінійного оператора
– одержуємо знайомий числовий запис лінійного оператора  .
.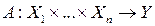 , де
, де  – нормовані простори.
– нормовані простори. , якщо
, якщо 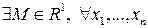 ,
, 
 .
. називається нормою А.
називається нормою А.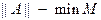 .
.
 – одиничний вектор з
– одиничний вектор з  ).
). .
. , якщо А обмежений, то одинична сфера переходить в еліпсоїд і норма співпадає з найбільшою піввіссю. З іншого боку, норма – верхня грань коефіцієнта розтягу векторів при даному відображенні.
, якщо А обмежений, то одинична сфера переходить в еліпсоїд і норма співпадає з найбільшою піввіссю. З іншого боку, норма – верхня грань коефіцієнта розтягу векторів при даному відображенні. – білінійне відображення, при
– білінійне відображення, при  маємо рівність
маємо рівність  і із нерівності Коші-Буняковського
і із нерівності Коші-Буняковського  .
. ,
, , тобто
, тобто  .
. ,
, .
. . У цьому випадку
. У цьому випадку  .
.
 .
. лінійний оператор, а
лінійний оператор, а 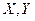 конечно вимірні нормовані простори, то А – має скінчену норму.
конечно вимірні нормовані простори, то А – має скінчену норму. , що діє з нормованого простору Х у нормований простір Y наступні умови рівносильні:
, що діє з нормованого простору Х у нормований простір Y наступні умови рівносильні: .
. . Нехай
. Нехай  (де
(де  - будь-яка точка з Х) в Х, тоді
- будь-яка точка з Х) в Х, тоді  , тобто А неперервний в
, тобто А неперервний в  , тобто у Х.
, тобто у Х. така, що
така, що 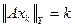 , і
, і  , тоді послідовність
, тоді послідовність 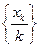 така, що
така, що  – це суперечить неперервності А, тобто припущення невірне.
– це суперечить неперервності А, тобто припущення невірне.
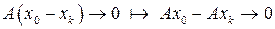 , тобто
, тобто  – А неперервний в
– А неперервний в  .
. ,
,  – множина неперервних полілінійних операторів.
– множина неперервних полілінійних операторів. . Якщо при цьому Y – повний, то L – повний нормований простір.
. Якщо при цьому Y – повний, то L – повний нормований простір. послідовність Коші, тобто
послідовність Коші, тобто  , що
, що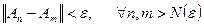 .
. послідовність Коші в Y, оскільки
послідовність Коші в Y, оскільки  , отже
, отже 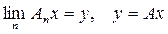 . Покажемо, що
. Покажемо, що  по нормі.
по нормі. ,
,  .
.
 тобто
тобто  , отже
, отже  .
. , то
, то 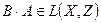 і
і .
.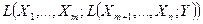 і
і  тобто
тобто . Покладемо
. Покладемо , тоді
, тоді 
 ізоморфний
ізоморфний 





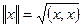 .
. ортонормований базис, то
ортонормований базис, то  .
. , а
, а  . Довести, що оператор
. Довести, що оператор 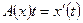 - лінійний оператор з
- лінійний оператор з  .
. , то загальний лінійний оператор
, то загальний лінійний оператор  з нормою
з нормою 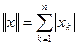 . Довести, що
. Довести, що 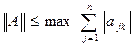 , де А – лінійний оператор з
, де А – лінійний оператор з  , а
, а  - відповідна матриця.
- відповідна матриця. (оператор добутку на функцію
(оператор добутку на функцію  )
)  - неперервна функція. Довести лінійність А та
- неперервна функція. Довести лінійність А та  .
.


