
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Практичне заняття №3 Тема: Похідні та диференціали вищих порядків. Формула Тейлора.Содержание книги
Поиск на нашем сайте
Основні відомості: 1. Визначення похідної та диференціала n-го порядку. 2. Формула Тейлора. 3. Розклад в ряд Маклорена основних елементарних функцій. Задачі: 1.1. За допомогою формули Лейбниця та основних формул: 1. 3. Розв’язати задачі: 1.2. 1.3. 1.4. Знайти 1.5. Знайти За допомогою формули Тейлора розв’язати задачі: 2.1. Нехай Довести, що Вказівка. Довести за допомогою індукції. 2.2. Нехай Вказівка: Розглянути
2.3. Розкласти в ряд Маклорена до
Завдання для самостійної роботи. Нехай 1. 2. 3. 4. 5. 6. 7. Розклавши функцію на найпростіші дроби знайти 8.
9. 10. 11. 12. 13. 14. Нехай Вважаючи 15. 16. 17. 18. Нехай 19. 20. 21. Нехай Вказівка.
22. Нехай
Розкласти за формулою Маклорена до 23. 24. 25. Практичне заняття №4 Тема: Формула Тейлора. Обчислення границь за допомогою формули Тейлора.
Основні відомості: 1. Фрмула Тейлора. 2. Остаточний член формули Тейлора в формі Лагранжа. 3. Розклад основних елементарних функцій. Задачі: Використовуючи розклад основних елементарних функцій розкласти функції в ряд Маклорена до 1.1. 1.2. Вказівка: Використовувати 1.3. Використовуючи метод неозначених коефіцієнтів розкласти функції виду 2.1. Розкласти 2.2. 2.3. Розкласти Вказівка: Використати розклад Обчислити границі: 3.1. 3.2. 3.3. Завдання для самостійної роботи. Розкласти в ряд Маклорена до 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. Вказівка: В задачах 12,13 записати функції у вигляді комбінації елементарних функцій. 14. 15. 16. 17. 18. 19. 20. 21. 22. 23. 24. 25. Лекція №2 Дослідження на монотонність та екстремуми. Випуклі функції. Правило Лопіталя. Дослідження монотонності. Наступна теорема легко доводиться за допомогою теореми Лагранжа та означення монотонності (див.[1,2] або доведіть самостійно). Теорема. Нехай функція Тоді: 1. 2. 3. 4. Необхідна і достатня умова локального екстремуму. Означення. Нехай
Теорема Ферма. (необхідна умова екстремуму) Якщо Доведення. аналогічне доведенню теореми Роля, якщо Теорема. (достатня умова екстремуму). Нехай функція 1. 2. 3. Доведемо випадок 1. Оскільки Перейдемо в нерівності до границі при Випадки 2 і 3 доведіть самостійно аналогічно доведенню випадку 1. Приклад. Застосовуючи останню теорему доведіть закон переломлення світла. Опуклі функції. Означення. Функція
Означення. Функція
Перефразуємо означення.
або Отже, функція
( Необхідна і достатня умова опуклості. Теорема. Для того, щоб диференційована на інтервалі Доведення Необхідність. Нехай
Переходячи до границі в нерівності при
Достатність. 1. 2.
Опуклість вгору доводиться аналогічно. Наслідок. Для того, щоб функція Теорема. (нерівність Йенсена). Якщо функція Доведіть самостійно за допомогою математичної індукції. Приклад.
Покладемо Підставляючи, отримаємо нерівність Гельдера:
або
Нерівність Коші. Для будь-яких
Доведення.
Ця нерівність показує, що нерівність трикутника в звичайній метриці в Правило Лопіталя. Теорема. Нехай функції 1. 2. буде існувати Доведення. Доведемо випадок 1.
Функції
Для будь-якої послідовності
Отже, за Гейне Інший випадок розгляньте самостійно.
|
||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 363; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.5 (0.009 с.) |


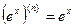 2.
2. 



 , якщо
, якщо  , а
, а  - незалежна змінна.
- незалежна змінна.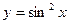 , а
, а  .
. .
. - двічі диференційована функція та
- двічі диференційована функція та 
 Довести, що
Довести, що  .
.

 .
. - тричі диференційована функція. Знайти
- тричі диференційована функція. Знайти  та
та  якщо:
якщо: .
. .
. .
. .
.
 - тричі диференційована функція.
- тричі диференційована функція.






 , де
, де  - многочлен.
- многочлен.
 , де
, де 



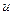 - функція від
- функція від  знайти
знайти  .
.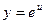 знайти
знайти  .
. та
та 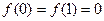 , при чому
, при чому 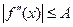 при
при  . Довести, що
. Довести, що  при
при  .
.
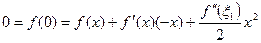
 - многочлен ступеня не вище
- многочлен ступеня не вище  . Довести, що
. Довести, що .
. :
:




 .
.
 та
та  :
: до
до 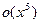 методом неозначених коефіцієнтів.
методом неозначених коефіцієнтів. розкласти до
розкласти до 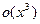 .
. до
до  .
. .
.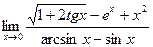


 .
. .
. .
.

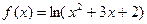




 розкласти до
розкласти до 

 розкласти до
розкласти до 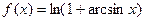 розкласти до
розкласти до  розкласти до
розкласти до  розкласти до
розкласти до  розкласти до
розкласти до 


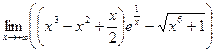

 і один раз диференційована на інтервалі
і один раз диференційована на інтервалі 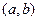 .
. не спадаюча на
не спадаюча на  не зростаюча на
не зростаюча на  строго зростає на
строго зростає на  строго спадає на
строго спадає на  і Е область визначення, тоді
і Е область визначення, тоді  називається локальним максимумом (мінімумом), якщо
називається локальним максимумом (мінімумом), якщо  - окіл
- окіл  такий, що
такий, що .
. і
і 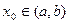 , а
, а  диференційована в
диференційована в  .
. .
. , тоді:
, тоді: - локальний максимум.
- локальний максимум.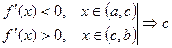 - локальний мінімум.
- локальний мінімум. - не екстремальна точка.
- не екстремальна точка. , то
, то  таких, що
таких, що  маємо
маємо  .
. , тоді
, тоді  оскільки
оскільки  неперервна
неперервна  )
)  . Аналогічно
. Аналогічно 
 . Таким чином, означення локального максимуму в точці с виконано (окіл
. Таким чином, означення локального максимуму в точці с виконано (окіл  ).
). називається опуклою вниз на
називається опуклою вниз на  якщо
якщо  і
і 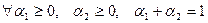 виконується нерівність
виконується нерівність .
. .
. ,
, 

 Тоді нерівність із першого означення набуде вигляду:
Тоді нерівність із першого означення набуде вигляду:



 .
.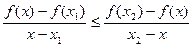 ,
,  ,
,  була опуклою вниз (вгору) необхідно і достатньо, щоб її похідна
була опуклою вниз (вгору) необхідно і достатньо, щоб її похідна  була зростаючою (спадаючою).
була зростаючою (спадаючою). і
і  і
і  будемо мати
будемо мати

 . Отже, із зростання
. Отже, із зростання  означення опуклості вниз виконується.
означення опуклості вниз виконується. .
. і
і  , то
, то  .
. ,
,  опукла вниз, отже
опукла вниз, отже .
. .
.





 виконується.
виконується. диференційовані на
диференційовані на 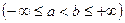 , причому
, причому  на
на  при
при  . Тоді в кожному з двох випадків
. Тоді в кожному з двох випадків при
при 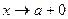 ,
, при
при 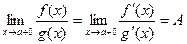 .
. ,
, 
 визначені на
визначені на  неперервні та диференційовані на
неперервні та диференційовані на  і задовольняють теорему Коші. Отже
і задовольняють теорему Коші. Отже 
 таке, що
таке, що або
або  ,
, 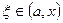
 існує послідовність
існує послідовність  і
і та
та  .
.



