
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лекція №10 Теорема про неявну функціюСодержание книги
Поиск на нашем сайте
1. Теорема про неявну функцію Нехай Приклад.
Частіше ця обставина не виконується, тобто при фіксованому х Розглянемо задачу. Нехай вираз Теорема. Нехай 1. 2. 3. 4. то знайдуться окіл 1) 2)Рівність 3) 4) f – неперервне в Доведення. Для спрощення запису можна вважати, що Розглянемо клас функцій Зауважимо, що Таким чином, пошук і дослідження неявно заданої функції Покажемо, що
В силу неперервності Таким чином, при будь-якому
тобто Для існування нерухомої точки
то Значить при На основі принципу про стискаюче відображення можна стверджувати: Неперервність Доповнення. Якщо разом з умовами теореми відомо, що у околі то функція
Доведення. Перевіримо безпосередньо, що лінійний оператор у правій частині рівності
Ці співвідношення написані з урахуванням того, що
Значить Приклади. 1. Нехай 2. 3. тоді існують околи 1. 2. 3. 4. 2. Нехай
Якщо 1. 3. тоді існують околи 1. 2. 3. 4. 2. Обернена функція. З теореми про неявну функцію безпосередньо випливає теорема про обернену функцію, оскільки знайти обернену функцію Теорема. Нехай Якщо Лекція №11 Умовні екстремуми
|
||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 608; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.006 с.) |

 і
і 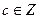 . Розглянемо вираз
. Розглянемо вираз  . Може статися, що для заданого х рівняння
. Може статися, що для заданого х рівняння  відносно
відносно  має розв’язок, і притому єдиний. В такому випадку це рівняння визначає функцію
має розв’язок, і притому єдиний. В такому випадку це рівняння визначає функцію  , яку називають неявною функцією, визначену рівнянням
, яку називають неявною функцією, визначену рівнянням  . Вона характеризується властивістю
. Вона характеризується властивістю 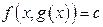 .
.
 – або не існує, або їх декілька, або нескінченно багато.
– або не існує, або їх декілька, або нескінченно багато. задовольняється у точці
задовольняється у точці 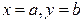 . Пропонується визначити, коли в околі точки
. Пропонується визначити, коли в околі точки  при кожному х існує єдиний розв'язок даного рівняння, тобто у випадку
при кожному х існує єдиний розв'язок даного рівняння, тобто у випадку  рівняння
рівняння  визначає деяку криву в
визначає деяку криву в 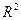 і ми хочемо виразити її у звичайній формі, представивши
і ми хочемо виразити її у звичайній формі, представивши  .
. – нормовані простори, причому
– нормовані простори, причому 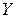 – повний;
– повний;  – окіл точки
– окіл точки  в
в  . Якщо відображення
. Якщо відображення  задовольняє умовам:
задовольняє умовам: ;
; – неперервне в точці
– неперервне в точці  ;
; визначене в
визначене в  і неперервне в
і неперервне в  ;
;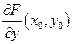 має обернений оператор;
має обернений оператор;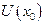 точки
точки 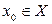 , окіл
, окіл  точки
точки  і відображення
і відображення  такі, що:
такі, що: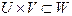 ;
; в
в  еквівалентна тому, що
еквівалентна тому, що  де
де  ;
; ;
; .
. .
.  .
.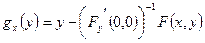
 , що залежать від параметра
, що залежать від параметра  і визначені на множині
і визначені на множині  . При
. При  - околу
- околу 
 – є відображення
– є відображення  .
. розв'язок рівняння
розв'язок рівняння  , тоді і тільки тоді, коли
, тоді і тільки тоді, коли  .
. зводиться до пошуку нерухомих точок відображення
зводиться до пошуку нерухомих точок відображення  – стискаюче відображення для фіксованого х. Дійсно, при довільному
– стискаюче відображення для фіксованого х. Дійсно, при довільному 
 диференційоване, що випливає з умови 3 і диференціювання складеної функції.
диференційоване, що випливає з умови 3 і диференціювання складеної функції.
 в точці
в точці 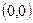 існує окіл
існує окіл  точки
точки  .
. і
і  за теоремою про скінчений приріст
за теоремою про скінчений приріст ,
, стискаюче.
стискаюче. повинно переводити повний простір у себе. Покажемо, що
повинно переводити повний простір у себе. Покажемо, що  , що при будь-якому
, що при будь-якому  відображення
відображення 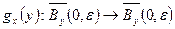 . Дійсно, спочатку по
. Дійсно, спочатку по  візьмемо
візьмемо 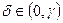 так, щоб при
так, щоб при 
 , (це можливо в силу неперервності
, (це можливо в силу неперервності 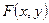 в
в  і
і  ). Якщо тепер
). Якщо тепер 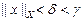 і
і 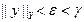 ,
,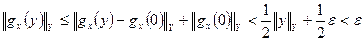 .
.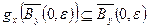 . Оскільки замкнена підмножина повного метричного простору повна, то куля
. Оскільки замкнена підмножина повного метричного простору повна, то куля  – повний метричний простір, в якому
– повний метричний простір, в якому 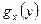 - утворене стискаюче відображення у себе.
- утворене стискаюче відображення у себе. існує єдина точка
існує єдина точка  , яка є нерухомою точкою відображення
, яка є нерухомою точкою відображення  . В силу основного співвідношення
. В силу основного співвідношення  має властивість 2, а значить і властивість 3, оскільки
має властивість 2, а значить і властивість 3, оскільки  в точці
в точці  випливає з властивості 2 (для f) і того, що
випливає з властивості 2 (для f) і того, що 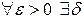 , що при
, що при 
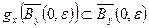 , тобто єдина нерухома точка
, тобто єдина нерухома точка  відображення
відображення 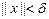 задовольняє умові
задовольняє умові  .
. існує частинна похідна
існує частинна похідна  неперервна в
неперервна в 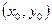 ,
,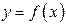 диференційована в
диференційована в  і
і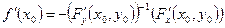 .
.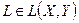 є похідною функції
є похідною функції  в точці
в точці 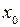 . Як і в теоремі для скороченого запису будемо вважати, що
. Як і в теоремі для скороченого запису будемо вважати, що  , тобто
, тобто  .
. де
де  при
при  .
. і того, що неперервність
і того, що неперервність  і
і 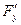 в
в  в цій точці. Покладемо
в цій точці. Покладемо  і
і  . Тоді враховуючи нерівність
. Тоді враховуючи нерівність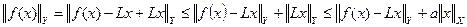 , можна продовжити першу оцінку
, можна продовжити першу оцінку  або
або при
при  в силу неперервності f в
в силу неперервності f в 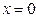 і
і  .
. , що і треба було довести.
, що і треба було довести. і
і  . Якщо
. Якщо існують в
існують в  і неперервні в
і неперервні в  ;
; ;
; ;
; і
і  і функція
і функція 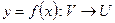 , що задовольняють умовам:
, що задовольняють умовам: ,
,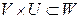 ,
, ,
, неперервна в
неперервна в 
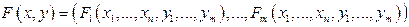


 існують в
існують в  і неперервні в
і неперервні в 
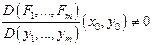 ,
,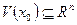 і
і  , в яких існує єдина функція
, в яких існує єдина функція  , що задовольняє умовам:
, що задовольняє умовам: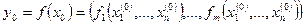 ;
; ;
;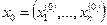 .
. для деякого гомеоморфізма
для деякого гомеоморфізма  все рівно, що розв’язати задачу про неявну функцію відносно х.
все рівно, що розв’язати задачу про неявну функцію відносно х. і
і  – повні нормовані простори і
– повні нормовані простори і  – неперервне диференційоване відображення відкритої множини
– неперервне диференційоване відображення відкритої множини 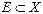 в
в  .
. і
і  – має обернений, то образ кожного околу точки а при відображенні f є околом точки
– має обернений, то образ кожного околу точки а при відображенні f є околом точки  . Існують такі відкриті множини А і В в Х і
. Існують такі відкриті множини А і В в Х і  .
.


