
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методика вивчення теми «Похідна» в шкільному курсі математикиСодержание книги
Поиск на нашем сайте
За програмою на тему «Похідна та її застосування» відводиться 16 год. Головна мета при вивченні даної теми: розглянути задачі, що приводять до похідної на основі їх узагальнення ввести означення похідної, розглянути її механічний і геометричний зміст. Довести формули похідних елементарних функцій та теореми про похідні суми, добутку, частки функцій. Розглянути похідну складеної функції. Навчити учнів обчислювати похідні з використанням формул та теорем. Розглянути застосування похідної до дослідження функцій на зростання, спадання, знаходження найбільших і найменших значень функції Учні повинні знати: означення похідної функції в точці; її механічний і геометричний зміст;таблицю похідних елементарних функцій;правила обчислення похідної суми, добутку, частки двох функцій;достатню умову зростання і спадання функцій, екстремумів функцій;на відрізку, застосування похідної в геометрії, фізиці. Навчити досліджувати властивості функцій і будувати їх графіки. У навчально-методичній літературі зустрічаються різні підходи до з’ясування поняття похідної. Це поняття дається учням: · або на основі задачі про дотичну до кривої; · або на основі задачі на визначення швидкості нерівномірного руху; · або на основі розгляду обох цих задач. Із задачею про миттєву швидкість, учні ознайомились вже в курсі фізики, і можливо, в курсі алгебри і початків аналізу при введенні поняття границі числової послідовності. На цьому етапі навчання розв’язання задачі про миттєву швидкість треба оформити в термінах і символах математичного аналізу (приріст аргументу і функції, границя функції), чітко відділяючи кроки міркувань, які розкривають зміст похідної і виконуватимуться далі під час виведення формул похідних різних функцій і доведення поносних теорем про похідні. Із задачею про дотичну можна ознайомити учнів пізніше, коли розглядатиметься геометричний зміст похідної та її застосування в геометрії. Розглядаючи задачу про миттєву швидкість, доцільно звернути увагу на те, що середня швидкість нерівномірного прямолінійного руху певним чином характеризує його, проте часто вона не задовольняє потреб практики. Щоб учні неформально сприймали означення миттєвої швидкості, треба на прикладі задачі з конкретними числовими даними показати, що значення середньої швидкості прямує до певної границі, яку й природно взяти за числове значення швидкості в даний момент часу. У всіх таких задачах доводиться визначати швидкість зміни значень певних функцій в залежності від зміни аргументу. В зв’язку з потребою узагальнити способи розв’язування подібних задач і було введене в математику поняття похідної функції y = ƒ(x) як швидкості зміни значень залежно від зміни аргументу Після вивчення даної теми учні повинні чітко розуміти розв’язок задачі про миттєву швидкість, вміти виділяти чотири кроки задачі. У наступному параграфі учні починають вивчати означення похідної, її механічний та геометричний зміст. Означення похідної формулюється за підручником [66]. Коли функція y = ƒ(х) має похідну в кожній точці x проміжку [a;b], то кожному значенню x відповідатиме певне значення похідної. Далі роботу можна організувати так, щоб один учень біля дошки, а решта самостійно в зошитах, провівши всі кроки міркувань, знайшли похідну функції ƒ(x)=5х2 – 2х. Наступний урок треба присвятити розв’язанню прикладів на обчислення похідних за означенням, аналогічних вміщеним у завд.1 підручника [66]. Перед ознайомленням учнів з геометричним змістом похідної необхідно, щоб учні чітко розуміли задачу про дотичну і бачили її практичне значення. Спочатку треба з’ясувати поняття дотичної до кривої. З цим поняттям учні зустрічалися в курсі геометрії, де дотичну означали як пряму, що має спільну точку з колом. Потрібно підвести учнів до того, щоб вони зробили висновок, що порядок розв’язування задачі на побудову дотичної такий. 1) Складаємо відношення Тепер треба розглянути обернене твердження, а саме: якщо функція ƒ(х) має похідну в точці х, то а) в цій точці є дотична до графіка функції, б) кутовий коефіцієнт її дорівнює похідній функції ƒ(х) в точці х. З розглянутих прикладів учні самі можуть зробити висновок, що коли функція має на певному інтервалі похідну, то вона на цьому інтервалі неперервна. В діючому підручнику це твердження подане у вигляді теореми, яка наочно випливає з геометричної суті похідної: якщо на певному інтервалі функція має похідну, то в кожній точці цього інтервалу можна провести дотичну. Учням вказують на те, що обернене твердження не завжди має місце, тобто функція може бути неперервною і не мати похідної, наприклад, вже знайома учням неперервна функція y =½x½не має похідної в точці x = 0. Перед вивченням правил диференціювання елементарних функцій слід з учнями повторити загальне правило диференціювання, засноване на означенні похідної. Треба їм пояснити, що загальне правило диференціювання є не що інше, як переказ самого означення похідної. Якщо яка-небудь функція ƒ(х) має похідну в точці х, то цю похідну завжди можна знайти, застосувавши загальне правило диференціювання. Далі треба учням пояснити, що незручно весь час застосовувати загальне правило диференціювання, бо на це потрібно багато часу. Для полегшення праці користуються спеціальними правилами для диференціювання часто вживаних функцій. Перед виведенням правил диференціювання слід сказати учням, що розглядатимемо лише такі функції, які мають похідну при всіх допустимих значеннях аргументу. Похідна сталої. Креслимо графік функції y = c. З графіка видно, що коли аргумент х дістає приріст Δх, то у не змінює своєї величини, отже приріст функції Δy завжди дорівнює нулю. Тоді Слід вимагати від учнів точного формулювання правила: Похідна від сталої величини дорівнює нулю. Доведення теорем добутку і частки є не обов’язковим. Це залежить від наявності часу і від роботи класу. Проте буде доцільно, щоб учні ознайомились з ними самостійно вдома. Зауважимо, що під час доведення теорем про похідні деякі учні формально переносять правило тотожних перетворень добутку одночлена на многочлен на перетворення, пов’язані з функціональною символікою, забуваючи про те, що в даному випадку букви u i ν позначають не змінні, а відношення (функції). Тому учням наголошують, що значення функцій u i ν та їх похідних у точці x позначаються коротко Для кращого запам’ятовування формули треба, щоб учні привчалися формулювати правило так, щоб словесний вираз відповідав письмовому запису. Ми говоримо і одночасно записуємо математичними символами: «похідна першої функції, помножена на другу без змін, плюс похідна другої функції, помножена на першу без змін». Теорема про похідну складеної функції і розв’язування вправ на обчислення похідних складених функцій викликають певні труднощі у багатьох учнів. Ці труднощі можна зменшити, якщо, формулюючи поняття складеної функції, ввести поняття проміжної залежної змінної. 3….
|
||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 1353; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.40.121 (0.008 с.) |

 .
.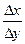 . 2) Знаходимо
. 2) Знаходимо  . 3) Проводимо через точку M пряму, що утворює з віссю OX кут a, тангенс якого дорівнює
. 3) Проводимо через точку M пряму, що утворює з віссю OX кут a, тангенс якого дорівнює 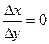 , бо чисельник завжди дорівнює нулю, а знаменник не дорівнює 0 (він лише прямує до 0). Коли ж
, бо чисельник завжди дорівнює нулю, а знаменник не дорівнює 0 (він лише прямує до 0). Коли ж  , бо коли змінна в процесі зміни дорівнює певному числу, то границя цієї змінної дорівнює тому самому числу. Отже, y′ = 0, тобто похідна функції y = c в будь-якій точці дорівнює нулю.
, бо коли змінна в процесі зміни дорівнює певному числу, то границя цієї змінної дорівнює тому самому числу. Отже, y′ = 0, тобто похідна функції y = c в будь-якій точці дорівнює нулю.


