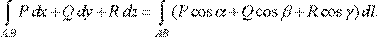Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Зв’язок мвж криволінійними інтегралами і і іі родуСодержание книги
Поиск на нашем сайте
Нехай
2. Поняття функцiї в сучасному курсi математики ЗНЗ. Рiзнi пiдходи до означення поняття функцiї, процес формування поняття функцiї Сучасний підхід: «Відношення між множинами X і У, при якому кожному елементу множини Х відповідає не більш одного елемента множини У, називається функцією». Це означення ширше класичного, бо значеннями величини в класичному означенні є число, а елементи множини це числа або будь-які інші об'єкти. В загальноосвітній школі це означення трактується вужче: «Функція -це залежність змінної х, при якій кожному значенню х відповідає єдине значення у». При цьому у основній школі під х і у розуміють тільки числові змінні. В окремих підручниках дають таке визначення функції. Якщо кожному значенню змінної х з деякої множини відповідає єдине значення змінної у, то таку залежність називають функціональною залежністю, або функцією. При цьому змінну х називають незалежною змінною або аргументом, змінну у - залежною змінною або функцією від аргументу. Існують дві найбільш різко відмінні методичні трактовки поняття функції: генетична і логічна. Генетична трактовка поняття функції заснована на розробці поняття функції. Найбільш істотними поняттями є такі: змінна величина, функціональна залежність змінних величин, формула, декартова система координат. Ø Позитивне: підкреслюється “динамічний “ характер поняття функціональної залежності, природно пов’язується з рештою змісту курсу алгебри, так як більшість функцій, які використовуються в ньому, виражаються аналітично і таблично. Ø Недоліки: поняття пов’язується з числовими функціями одного числового аргументу. Логічне трактування поняття функцій виходить із положення про те, що будувати поняття функції треба в рамках поняття алгебраїчної системи. Функція при такому підході виступає у вигляді відношення спеціального виду між двома множинами, що задовольняє умові функціональності. Ø Достоїнство: узагальненість поняття і можливості встановлення зв’язків в навчанні математики. Але поняття функції в середній школі пов’язувалось, головним чином, з числовими функціями одного числового аргументу, тобто тією областю, в якій воно простіше формується на генетичній основі. В цьому зв’язку в шкільних підручниках поняття функції означається як залежність однієї змінної від іншої. В школі це поняття трактується уже: функція – це залежність змінної Y від змінної Х, при якому кожному значенню Х відповідає єдине значення. Y. При цьому в дев’ятирічній школі під Х і Y розуміють тільки числа. В сучасному шкільному курсі в якості ведучого прийнятий генетичний підхід до поняття функції.
|
||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 506; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.91.130 (0.008 с.) |





 напрямлена просторова крива з початком
напрямлена просторова крива з початком 

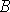

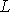



 точки дотику
точки дотику 




 з проекціями
з проекціями