
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Використання нових інформаційних технологій навчання математикиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Нові інформаційні технології— сукупність методів і технічних засобів збирання, організації, збереження, опрацювання, передачі й надання інформації, що розширює знання людей і розвиває їхні можливості щодо керування технічними й соціальними проблемами. Застосування комп'ютерної техніки робить уроки математики яскравими, насиченими.На цих уроках кожен учень працює активно, в учнів розвивається допитливість, пізнавальний інтерес. Комп'ютер дозволяє підсилити мотивацію навчання: - шляхом активного діалогу учня з комп'ютером, - розмаїтістю й барвистістю інформації (текст + звук + колір + анімація), - шляхом орієнтації навчання на успіх (дозволяє довести рішення будь-якого завдання, опираючись на необхідну підказку), - використовуючи ігрову форму спілкування людини з машиною, - витримкою, спокоєм і «дружністю» машини стосовно Процес організації навчання школярів з використанням ІКТ дозволяє: * Активізувати пізнавальну діяльність учнів * Візуалізувати навчальний матеріал * Індивідуалізувати процес навчання * Здійснювати моніторингові відстеження результативності навчання * Створити комфортні психологічні умови для учнів при відповіді на питання, організувати самоконтроль * Забезпечити розвиток творчої активності школярів * Створити бібліотеку навчального електронного приладдя * Використовувати інформаційну базу глобальної мережі Інтернет та локальну шкільну мережу * Реалізувати входження учня у реальний світ дорослих, у виробничу діяльність людини сучасного інформаційного цифрового суспільства в процесі роботи учня й учителя з використанням комп'ютерних технологій При плануванні уроків математики з використанням ІКТ треба враховувати: • наявний набір комп’ютерного та мультимедійного обладнання, • наявність програмно-методичного комплексу до підручника, що відповідає діючій програмі, • наявність інструментальних середовищ, • наявність програм-тренажерів, • готовність учнів до роботи з використанням комп'ютера, • можливості учня використовувати комп'ютерні технології поза класом. Комп’ютерні презентації, виконані в різних програмних середовищах, органічно вписуються в будь-який урок, ефективно допомагають учителю за мінімальний час самостійно виготовити мультимедійний посібник до уроку, що унаочнює навчальний матеріал, дає можливість провести математичний диктант і його перевірку, продемонструвати способи розв’язання завдань тощо. Причому достатньо одного лише комп’ютера та проектора для використання презентацій на уроці математики. Формати використання ІКТ при вивченні математики:
• самостійне навчання учнів; • використання тренінгових (тренувальних) програм; • використання діагностичних і контролюючих матеріалів; • виконання домашніх самостійних і творчих завдань; • використання комп'ютера для обчислень, побудови графіків; • використання програм, що імітують досліди, лабораторні роботи, застосування теорії у практичній діяльності людини; • використання ігрових і цікавих програм; • використання інформаційно-довідкових програм. Критерії оцінок уроку з використанням ІКТ: 1. Особистий внесок учителя в розробку уроку з використанням ІКТ 2. Форма використання програмного забезпечення 3. Організація діяльності учнів на уроці 4. Рівень методичної підготовки вчителя в області використання засобів ІКТ 5. Дотримання санітарно - гігієнічних вимог 6. Вплив інформаційних технологій на результативність 7. Індивідуалізація навчання за рахунок використання засобів ІКТ
Знайти екстремуми
Обчислити ранг
Вільні коливання струни Означення. Струною називають тверде тіло, довжина якого значно перевищує інші його розміри. Якщо u (x, t) – відхилення від положення рівноваги точки струни з абсцисою x в момент часу t і струна однорідна то рівнянням є
Означення. Рівняння при Хід хвильового процесу залежатиме від його початкового стану та початкових швидкостей. При розгляді задачі про коливання струни додаткові умови можуть бути двох видів: початкові та кінцеві (або крайові). Початкові умови показують, в якому стані перебувала струна в момент початку коливання. Зручніше за все вважати, що струна початку коливатися в момент часу (t = 0). Первинне положення точок струни задається умовою u│t=0= f (x) А початкова швидкість
який задовольняє початкові при
Оскільки початкові умови (задані в точках
Підставляючи загальний розв’язок в крайову умову
Шукаємо нетривіальні розв’язки рівняння (1), які задовольняють крайові умови (3), у вигляді
Підставивши (5) у рівняння (1) і розділивши змінні, одержимо остання рівність можлива тоді і тільки тоді, коли
Підставивши (5) у крайові умови (3), одержимо
Таким чином, нам потрібно знайти ненульові розв’язки рівняння (6) і крайової задачі (7), (8). Задача (7), (.8) не для всяких Задача (7), (8) знаходження власних значень і власних функцій називається задачею Штурма-Ліувілля.
|
||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 536; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.179.210 (0.007 с.) |




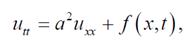
 називають рівняннямвимушених коливань струни. При
називають рівняннямвимушених коливань струни. При  отримуємо рівняння вільних
отримуємо рівняння вільних 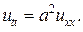 (1)
(1)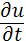 │t=0=
│t=0= 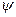 (x) Тобто приходимо до умов
(x) Тобто приходимо до умов  Інший характер мають крайові умови. Вони показують, що відбувається на кінцях струни в увесь час коливань. І простому випадку, коли кінці струни закріплені (початок струни - на початку координат, а кінець - у точці (t, 0)), функції и(х,t) буде підкорятися умовам
Інший характер мають крайові умови. Вони показують, що відбувається на кінцях струни в увесь час коливань. І простому випадку, коли кінці струни закріплені (початок струни - на початку координат, а кінець - у точці (t, 0)), функції и(х,t) буде підкорятися умовам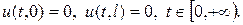 Нехай потрібно знайти розв’язок задачі
Нехай потрібно знайти розв’язок задачі 
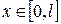 та крайові умови
та крайові умови 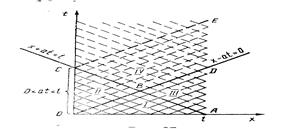 Для побудови розв’язку такої мішаної задачі застосовуємо метод характерис-тик.
Для побудови розв’язку такої мішаної задачі застосовуємо метод характерис-тик.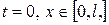 , то розвязок задається дається формулою Д’Аламбера – на рис. область I
, то розвязок задається дається формулою Д’Аламбера – на рис. область I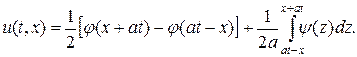
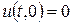 , знаходимо відображену хвилю
, знаходимо відображену хвилю 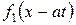 за відомою падаючою хвилею
за відомою падаючою хвилею 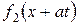 в точках відрізка
в точках відрізка 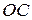 . Це дає можливість побудувати розв’язок розглядуваної мішаної задачі в області II (трикутник
. Це дає можливість побудувати розв’язок розглядуваної мішаної задачі в області II (трикутник 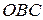 ). Використовуючи другу крайову умову
). Використовуючи другу крайову умову 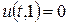 ,знаходимо відображену хвилю
,знаходимо відображену хвилю 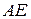 . Це дає можливість знайти шуканий розв’язок в областях III і IV (трикутник
. Це дає можливість знайти шуканий розв’язок в областях III і IV (трикутник 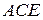 ). Повторюючи вищеприведені міркування, можна побудувати розв’язок мішаної задачі у всій області
). Повторюючи вищеприведені міркування, можна побудувати розв’язок мішаної задачі у всій області  . Розв’язок задачі може бути знайдений і за методом Фурє. Нехай необхідно знайти розв’язок диференціального рівняння
. Розв’язок задачі може бути знайдений і за методом Фурє. Нехай необхідно знайти розв’язок диференціального рівняння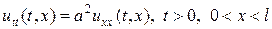 , (1) який задовольняє рівняння
, (1) який задовольняє рівняння 
 (2) і крайові умови
(2) і крайові умови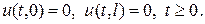 (3)В силу умов узгодженості
(3)В силу умов узгодженості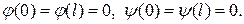 (4)
(4)
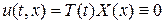 (5)
(5)
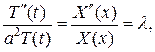
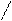
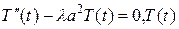 º 0, (6)
º 0, (6)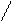

 º 0.(7)
º 0.(7)
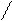 Оскільки
Оскільки 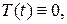 то із останніх рівностей маємо
то із останніх рівностей маємо  (8)
(8)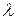 має нетривіальні розв’язки. Означення. Ті значення параметра
має нетривіальні розв’язки. Означення. Ті значення параметра 


