
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методика вивчення алгебраїчних i трансцендентних функцiй у курсi математики ЗНЗ.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Поняття функціональної залежності є одним з центральних в математиці, Вивчення поведінки функцій і побудова їх графіків є важливим розділом шкільного курсу. Починаючи з 7 класу середньої школи йде поступове вивчення властивостей функцій та функціональних залежностей. Розглядаються різні класи функцій: починаючи з найпростіших лінійних функцій і їх графіків, потім квадратичні функції, функції оберненої пропорційності і дробово-лінійні функції, які відносимо до алгебраїчних У старших класах учні вивчають трансцендентні функції. Трансцендентні функції – це клас показникових, тригонометричних, логарифмічних, обернених тригонометричних та інших функцій, які не являються алгебраїчними. В 10 класі вводяться тригонометричні функції, і в 11 класі нарешті, показникові і логарифмічні функції. Всі ці функції розглядаються тільки як функції однієї змінної, причому самі змінні не виходять за рамки безлічі дійсних чисел. У результаті вивчення курсу математики учні повинні: ознайомити учнів 8-го класу з властивостями і графіком функції у= Функція у= Степенева функція Вивченню степеневої функції передує розгляд парних і непарних функцій. Ці поняття дають змогу зразу систематизувати степеневі функції за ознакою парності чи непарності, допомагають учням усвідомити спільне й відмінне у розміщенні на координатній площині графіків степеневих функцій з парним і відповідно непарним показниками.В основній школі розглядається степенева функція лише з натуральним показником. Головна мета вивчення її — узагальнити вивчені відомості про функції та їх графіки, розглянути деякі нові властивості функцій. Зважаючи на те, що учні вже мають достатній досвід оперування поняттям функції і відповідною термінологією, треба почати безпосередньо з означення.Властивості степеневої функції доцільно систематизувати в таблиці, де обов'язково вміщені графіки видозмін цієї функції. Введення поняття тригонометричних функцій числового аргументу. Насамперед потрібно згадати означення тригонометричних функцій кута і поширити їх на будь-яку градусну міру, ввести кут повороту. Крім того, слід переконати учнів, що існує відповідність між множиною дійсних чисел і множиною точок одиничного кола, для чого попередньо виконати таку вправу. Основна мета - вивчити властивості тригонометричних функцій, навчити учнів будувати їх графіки. Першою тригонометричної функцією, з якою ознайомлюються учні, стає функція y = cosx, Вивчення даних функцій починається з повторення визначення синуса, косинуса і тангенса довільного кута які були введені в 9 класі. Так як функція y = cosx періодична з періодом 2p, то досить побудувати її графік на якому-небудь проміжку довжиною 2p. Крім того досить побудувати її графік на відрізку 0 £ х £ p, а потім симетрично відобразити щодо осі Оу. Перш ніж перейти до побудови графіка, доводиться, що функція y = cosx убуває на відрізку 0 £ х £ p. Доведене тут властивість дозволяє зробити висновок про можливість побудови графіка функції на цьому відрізку і поширенні його на всю числову пряму. Для побудови функції y = sinx використовують формулу: функції y = sinx можна отримати зрушенням графіка функції y = cosx вздовж осі абсцис вправо на проміжку 2.5. Показникова функція.
4. Розв’язати рівняння в повних диференцiалах:
1. Функції багатьох змінних, неперервність та диференційованість функції багатьох змінних. Теорема про рівність мішаних похідних. Розглянемо функцію Оз. функцією двох змінних Оз.. Функція Функція Для функції багатьох змінних, як і для функції однієї змінної, доводять такі твердження: Т. сума і добуток двох неперервних на множині G функцій є неперервними на G функціями; Т відношення двох неперервних на G функцій є неперервною функцією в усіх точках множини G, в яких знаменник не перетворюється в нуль. Оз. Нехай функція або Нехай функція
то вона називається частинною похідною функції
Згідно з означ. при знаходженні частинної похідної Для функції
Якщо існує частинна похідна за x від функції Таким чином, за означенням
Якщо існує частинна похідна від функції Отже, за означенням
Для функції двох змінних
Означ. Частинні похідні другого і вище порядків функції
Теорема 2 (існування частинних похідних диференційовної функції). Якщо функція Теорема 3 (достатні умови диференційовності). Якщо функція 2. Методика розв’язування геометричних задач на побудову з допомогою циркуля і лінійки. Під задачею на побудову розуміють вимогу: побудувати за допомогою інструментів геометричну фігуру, яка б задовольняла певні задані умови. Розв’язати задачу на побудову означає звести її до скінченого числа елементарних побудов, які виконуються за допомогою циркуля і лінійки, на основі аксіом конструктивної геометрії. Основними неозначуваними поняттями в геометрії вважають точки, прямі і площини, а також основні співвідношення між ними – належати, лежати між і бути рівними. Усяке інше поняття в геометрії зводиться до основних за допомогою означень. Схема розв’язування задач на побудову складається з чотирьох етапів: АНАЛІЗ – це відшукання способу розв’язування задачі на основі закону про єдність аналізу та синтезу, це план розв’язування задачі (усвідомлення умови задачі, зв’язків між даними і шуканими величинами). ПОБУДОВА – відповідно до плану, складеного під час аналізу, за допомогою вказаних інструментів виконуємо побудову шуканої фігури за елементами, даними в умові задачі. ДОВЕДЕННЯ – це усвідомлення і перевірка правильності розв’язку задачі. ДОСЛІДЖЕННЯ – це етап, на якому визначаємо, для яких саме даних задача має розв’язки, і якщо має, то скільки їх, чи все зроблено добре, що можна зробити інакше,як діяти за інших умов. У будь-якій задачі на побудову потрібно за якими-небудь даними фігурам побудувати шукану фігуру, що задовольняє ті або інші умови. При цьому вказується (тобто формулюється явно або мається на увазі), за допомогою яких креслярських інструментів слід виконати побудова шуканої фігури. У шкільному курсі геометрії звичайно розглядаються задачі на побудову за допомогою циркуля й лінійки. Передбачається, що лінійка як інструмент геометричних побудов не має масштабних ділень і з її допомогою можна провести пряму, що проходить через дві дані або побудовані точки. Ніяких інших операцій виконати лінійкою не можна. За допомогою циркуля як інструмента геометричних побудов можна описати кло із центром у даній або побудованій точці й радіусом, рівним даному або побудованому відрізку. Сформуємо у загальному виді постановку задачі на побудову. Дана кінцева множина основних побудованих фігур При розв'язуванні задач на побудову часто доводиться "довільно вибирати" довільні точки, що як належать, так і не належать побудованим прямим, окружностям, а також відрізкам і променям. Можливість вибору довільних побудованих точок, що належать побудованим прямим або окружностям, не скінченне. Можливість вибору точок, що не належать побудованим прямим і окружностям, можна обґрунтувати за допомогою аксіом геометрії. Аналіз або пошук розв'язку задачі полягає у встановленні залежностей між даними фігурами й шуканою фігурою з метою знаходження способу розв'язування задачі. Для проведення аналізу задачу важаємо розвязаною й виконують "від руки" креслення, що зображує шукану й дані фігури. Потім вивчають шукану фігуру і її зв'язку з даними задачі, поки не стане ясна послідовність побудов, що веде до розв'язку. У ряді випадків доцільно виділити точку, пряму або відрізок (так званий основний елемент побудови), побудова якого приводить до побудови шуканої фігури. Побудова полягає в послідовнім перерахуванні тих побудов (найпростіших і основних), які треба виконати для розв'язування задачі. При цьому виконується креслення, тобто фактично здійснюється крок за кроком побудова шуканої фігури за допомогою циркуля й лінійки. Доведення полягає в тому, щоб установити, що побудована фігура дійсно задовольняє всім умовам, поставленим у Дослідження полягає в тому, щоб відповісти на запитання: 1)Чи при всякому виборі даних задача має розв'язок, тобто шукану фігуру можна побудувати циркулем і лінійкою? 2) Скільки різних розв'язків має задача при кожному можливому виборі даних? Задача. Побудувати трикутник сторони якого відповідно дорівнюють даним відрізкам а, b і с. Розв'язок. Проведемо яку-небудь пряму й відкладемо відрізок АВ, дорівнює відрізку с. Далі побудуємо два кола (А, b) і (В, а). Нехай С - одна із точок перетинання цих окружностей. З'єднавши точки А, С і В, з відрізками, одержимо шуканий трикутник АВС. Виникає питання:чи при будь-яких заданих відрізках а, b і і с задача має розв'язок? Доведемо, що якщо c Доведемо, що трикутник АВС, що задовольняє умовам задачі, можна побудувати. За побудовою АВ = с, тому АВ < а + b. Але, з іншого боку, якщо, наприклад, a Ясно, що можна побудувати нескінченна множина трикутників, сторони яких відповідно дорівнюють даним відрізкам. Але будь-які два з них рівні по трьом сторонам, тому ми вважаємо, що якщо дана задача на побудову має розв'язок, то вона має тільки один розв'язок.
|
||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 1589; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.013 с.) |

 . Вивчення елементарних функцій в основній школі здійснюється переважно на конкретно-індуктивному рівні, без строгих доведень. Базою для встановлення властивостей функції виступає графік, а простіші перетворення графіків дають змогу порівнювати властивості різних видозмін функцій. Отже, необхідно приділити достатню увагу початковому ознайомленню з функцією у=х2 ісформувати в учнів чіткі уявлення про її графік і властивості. Але треба забезпечити логічний перехід від розгляду квадратного тричлена до квадратичної функції у загальному вигляді. З цією метою виклад матеріалу починаємо з означення: квадратичною функцією називають функцію, яку можна задати формулою виду у=ах2+bх+с, де х — незалежна змінна, a, b і с — деякі числа, причому а
. Вивчення елементарних функцій в основній школі здійснюється переважно на конкретно-індуктивному рівні, без строгих доведень. Базою для встановлення властивостей функції виступає графік, а простіші перетворення графіків дають змогу порівнювати властивості різних видозмін функцій. Отже, необхідно приділити достатню увагу початковому ознайомленню з функцією у=х2 ісформувати в учнів чіткі уявлення про її графік і властивості. Але треба забезпечити логічний перехід від розгляду квадратного тричлена до квадратичної функції у загальному вигляді. З цією метою виклад матеріалу починаємо з означення: квадратичною функцією називають функцію, яку можна задати формулою виду у=ах2+bх+с, де х — незалежна змінна, a, b і с — деякі числа, причому а  0. Якщо b = 0, дістаємо функцію виду у=ах2+с; якщо с=0, матимемо у = ах2+bх; якщо b=0, с=0, то у = ах2. Якщо у функції у=ах2 коефіцієнт а= 1, матимемо уже відому нам функцію у=х2. Залежність у = х2 є квадратичною функцією найпростішого виду. Далі розглядаємо функцію у = ах2 та її графік.
0. Якщо b = 0, дістаємо функцію виду у=ах2+с; якщо с=0, матимемо у = ах2+bх; якщо b=0, с=0, то у = ах2. Якщо у функції у=ах2 коефіцієнт а= 1, матимемо уже відому нам функцію у=х2. Залежність у = х2 є квадратичною функцією найпростішого виду. Далі розглядаємо функцію у = ах2 та її графік. для k>0 і k <0 у
для k>0 і k <0 у . Ця формула показує, що графік
. Ця формула показує, що графік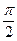
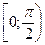 , А потім поширюється на всю числову пряму. Для цього доводиться, що функція y = tgx зростає на
, А потім поширюється на всю числову пряму. Для цього доводиться, що функція y = tgx зростає на



 ,
, 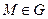 , яка кожній точці М множини G (площини або простору) ставить у відповідність деяке число
, яка кожній точці М множини G (площини або простору) ставить у відповідність деяке число 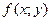 , де х,у – координати точки
, де х,у – координати точки  .
. ,
,  , функція двох змінних х і у, визначена для будь-яких значень змінних х, у, тобто на всій координатній площині R2. Вона кожній точці
, функція двох змінних х і у, визначена для будь-яких значень змінних х, у, тобто на всій координатній площині R2. Вона кожній точці 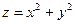
 , якщо для будь-якої послідовності точок
, якщо для будь-якої послідовності точок  такої, що
такої, що 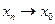 ,
,  при
при  , послідовність
, послідовність  .
. , крім, може, самої точки
, крім, може, самої точки  ,
,  , якщо для будь-якої послідовності точок
, якщо для будь-якої послідовності точок 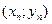 , таких що
, таких що 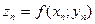 ,
,  , збігається до числа А. У цьому разі пишуть
, збігається до числа А. У цьому разі пишуть 
 при
при  де
де 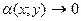 при
при  визначена в деякому околі точки
визначена в деякому околі точки  . Надамо змінній x приросту
. Надамо змінній x приросту  , залишаючи змінну
, залишаючи змінну 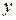 незмінною, так, щоб точка
незмінною, так, щоб точка  належала заданому околу.Величина
належала заданому околу.Величина  - називається частинним приростом функції
- називається частинним приростом функції 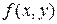 за змінною x.Аналогічно вводиться частинний приріст
за змінною x.Аналогічно вводиться частинний приріст  функції за змінною
функції за змінною  .Якщо існує границя
.Якщо існує границя  ,
,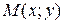 за змінною x і позначається одним із таких символів:
за змінною x і позначається одним із таких символів:  Аналогічно частинна похідна функції
Аналогічно частинна похідна функції  позначається:
позначається: 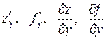 .
. обчислюють звичайну похідну функції однієї змінної x, вважаючи змінну
обчислюють звичайну похідну функції однієї змінної x, вважаючи змінну  сталою вважається змінна x.
сталою вважається змінна x. n змінних можна знайти n частинних похідних:
n змінних можна знайти n частинних похідних: , де
, де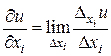 ,
,  .
.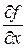 , то її називають частинною похідною другого порядку від функції
, то її називають частинною похідною другого порядку від функції  або
або  .
. або
або 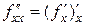 .
. , або
, або  .
. або
або  .
.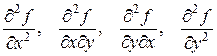 .
. Теорема (про мішані похідні).Якщо функція
Теорема (про мішані похідні).Якщо функція 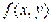 визначена разом із своїми похідними
визначена разом із своїми похідними 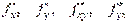 в деякому околі точки
в деякому околі точки  , причому похідні
, причому похідні  неперервні в точці
неперервні в точці  , то в цій точці
, то в цій точці 
 диференційовна в точці
диференційовна в точці  та
та 

 і ці похідні неперервні в точці М, то функція
і ці похідні неперервні в точці М, то функція  ,
,  ,...,
,...,  і описана властивість, що характеризує шукану непобудовану основну фігуру Ф. Потрібно, використовуючи аксіоми геометрії, одержати кінцеву множину основних побудованих фігур, що містить фігуру Ф.
і описана властивість, що характеризує шукану непобудовану основну фігуру Ф. Потрібно, використовуючи аксіоми геометрії, одержати кінцеву множину основних побудованих фігур, що містить фігуру Ф. а й c
а й c 


